Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Bernoulli's Equation and History
Unlock Audio Lesson
Today, we will explore the Bernoulli Equation, a pivotal tool in fluid mechanics. It originated in the 18th century and radically changed how engineers approached fluid flow problems.
Could you explain how the Bernoulli Equation simplified fluid flow analysis?
Absolutely! The equation helps us relate pressure, velocity, and height along a streamline, providing a clearer framework for analyzing fluid behaviors. Remember — Bernoulli's principle emphasizes conservation of energy in fluid motion.
What's the significance of the year 1752 in this context?
1752 marks when Bernoulli published his work, which laid the foundation for many modern fluid dynamics applications. Let's remember 1752 as the start of our journey into fluid mechanics!
So, it's like the birth year of a discipline?
Exactly! It’s the birth of fluid dynamics as we know it.
And how does this relate to its practical applications today?
Great question! The principles we learn now are applied in designing everything from cars to airplanes, impacting efficiency and safety.
To summarize, we’ve connected Bernoulli’s Equation with its historical significance and real-world applications. Remember, it is core to understanding fluid mechanics!
Understanding Pressures: Static, Dynamic, and Stagnation
Unlock Audio Lesson
Moving on, let’s tackle the different types of pressures in fluid mechanics. What do you think static pressure is, and how does it function?
Is it the pressure exerted by a fluid at rest?
Correct! Static pressure acts on the fluid at a stationary point. Now, how about dynamic pressure?
I think that's the pressure due to the fluid's motion.
Exactly! Dynamic pressure relates to the fluid’s velocity. Together, these create what we call stagnation pressure, when fluid velocity reaches zero momentarily. Can anyone remind me the formula for stagnation pressure?
Is it P = P_static + ½ρV²?
That's right! This formula is significant for applications like aircraft wing design, where we measure airspeed. Use the acronym 'PSD' to remember: Pressure, Static, Dynamic.
Can you explain more about how we measure these pressures in practice?
Certainly! We utilize devices like piezometers and pitot tubes to measure these pressures effectively, which in turn helps us analyze flows.
To recap: we have static pressure, dynamic pressure, and stagnation pressure, each serving a unique role in fluid dynamics.
Energy Gradient and Hydraulic Gradient Lines
Unlock Audio Lesson
Next, let’s dive into energy gradient lines and hydraulic gradient lines. Can anyone explain the difference?
I think energy gradient lines consider all forms of energy, while hydraulic gradient lines focus only on pressure and elevation.
Exactly! The energy gradient line combines flow energy, kinetic energy, and potential energy. What about hydraulic gradient lines?
They represent the height of fluid in relation to static pressure and elevation.
Correct! The hydraulic gradient line is fundamental in pipe flow analysis. Both lines demonstrate how energy transforms within the flow.
Why is it important to understand energy and hydraulic gradients?
Good question! Understanding these concepts aids us in designing efficient piping systems and predicting where energy losses occur.
So, to summarize, the energy gradient line encompasses all energy forms, while the hydraulic gradient line focuses on pressure and elevation alone.
Coefficient of Discharge and Real-World Applications
Unlock Audio Lesson
Now let’s examine the coefficient of discharge, or C_d. Why is it important in our calculations?
It helps us compare actual discharge to theoretical discharge, right?
Exactly! C_d takes into account energy losses due to friction and turbulence in practical applications. Can anyone think of a real-world example?
One example would be water flowing through an orifice meter?
Right! Understanding how to calculate C_d allows us to better predict flow behavior in systems such as pipes and channels.
How do we actually calculate this coefficient?
We calculate it by dividing the actual discharge by the theoretical discharge derived from the Bernoulli Equation.
To summarize, the coefficient of discharge is vital for accurate flow predictions, particularly in real-world systems!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces the Bernoulli Equation and its historical importance, explains its application in real fluid flow problems, and discusses essential concepts like kinetic energy correction factors and various pressures involved.
Detailed
Detailed Summary
The Bernoulli Equation, first suggested by Daniel Bernoulli in 1752, plays a fundamental role in fluid mechanics, particularly during the industrial revolution, where it enabled crucial advancements in pipe and channel flow design. This section outlines the usefulness of the Bernoulli Equation in solving fluid dynamics problems, emphasizing its applications through hydraulic gradient lines, energy gradient lines, and the incorporation of correction factors.
Key considerations include the definition of static, dynamic, and stagnation pressures, as well as an exploration of energy losses in systems like pumps and turbines. Furthermore, the section discusses practical applications, such as the analysis of vehicles' drag force and how design shape modifications have drastically improved fuel efficiency. Finally, the relationship between theoretical discharge and actual discharge is examined through the concept of the coefficient of discharge (C_d), highlighting the significance of real-world implications when applying the Bernoulli Equation.
Youtube Videos
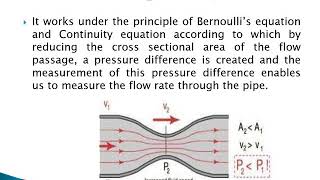
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Welcome all of you for this very interesting lecture on Bernoulli Equation and its Applications. The last class we discussed about Bernoulli equation starting from its history. Briefly, I can say that because of the Bernoulli equation, having a simplification to the fluid flow problems, the industrial revolutions that happened in Europe contributed significantly to the design of pipe flow and channel flow after this equation was suggested long back in 1752.
Detailed Explanation
The Bernoulli equation is a fundamental principle in fluid mechanics that describes the behavior of fluid flow. It simplifies complex fluid flow problems and has played a key role in advancements such as those seen during the industrial revolution in Europe. This equation, proposed by Daniel Bernoulli in 1752, helps engineers design systems related to pipes and channels by predicting how fluids will behave under various conditions.
Examples & Analogies
Imagine you are trying to understand how a garden hose works. The Bernoulli equation is like a recipe that tells you how the pressure, speed, and height of water in the hose interact. Just as following a recipe can help you bake a cake, using the Bernoulli equation helps engineers build systems that efficiently transport water.
Applications of Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Today, I will give a simple representation of the Bernoulli equation and how we can use it for real fluid flow problems, including systems with pumps and turbines. We will also explore applications such as kinetic energy correction factors, static, dynamic, and stagnation pressures, and hydraulic gradient and energy gradient lines.
Detailed Explanation
The Bernoulli equation has various applications in engineering, especially in systems involving fluid flow like pumps and turbines. It allows for the consideration of factors like correction for kinetic energy when flow is non-uniform. Understanding different types of pressures—static, dynamic, and stagnation—allows engineers to make better designs, while concepts like hydraulic and energy gradient lines help visualize and analyze energy in flowing fluids.
Examples & Analogies
Think about a water slide at an amusement park. Engineers use principles similar to the Bernoulli equation to design slides that are exciting yet safe. By understanding how water moves and where pressure points are, they can build slides that thrill riders while preventing risky situations. Just as understanding a water slide's design makes the experience more enjoyable, comprehending the Bernoulli equation opens up many possibilities in fluid mechanics.
Pressure Types in Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
I will define the three different types of pressures: static, dynamic, and stagnation pressures. These definitions are crucial for applying Bernoulli's principle effectively.
Detailed Explanation
In fluid dynamics, understanding pressure types is essential. Static pressure is the pressure exerted by a fluid at rest or the pressure measured at a certain point of a flowing fluid. Dynamic pressure arises from the motion of the fluid and relates to the kinetic energy of the fluid particles. Stagnation pressure is what you measure when you bring the fluid to rest; it combines both static and dynamic pressure and represents the total energy at a point in the flow.
Examples & Analogies
Imagine holding a garden hose. When the water is flowing, you feel it push against your hand; that feeling is like static pressure. If you were to block the end of the hose, the water would build up pressure until you release it—this is akin to stagnation pressure. Dynamic pressure can be thought of as the force of the water moving quickly out of the hose. Each pressure type gives you vital information about the fluid's behavior.
Energy Gradient and Hydraulic Gradient Lines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let’s examine energy gradient lines and hydraulic gradient lines. The total energy along a streamline is constant, and these lines help visualize energy changes throughout the flow.
Detailed Explanation
Energy and hydraulic gradient lines are helpful tools in fluid mechanics. They graphically represent how energy changes in a flowing fluid and help determine where energy losses occur. The energy gradient line reflects the total energy, including pressure, kinetic, and potential energy, while the hydraulic gradient line typically represents just the pressure and elevation heads. By examining these lines, engineers can diagnose issues in flow systems and make improvements.
Examples & Analogies
Consider a roller coaster. The energy gradient line helps us visualize how energy transforms as the car moves up and down hills. Just like the coaster must lose energy to move up to new heights, fluids lose energy as they flow through pipes and channels. Understanding these gradients helps engineers design safe and efficient water distribution systems, much like roller coasters are designed for fun and safety.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Bernoulli Equation: It relates the pressure, velocity, and elevation head of a fluid in motion.
-
Pressure Types: Understanding static, dynamic, and stagnation pressures allows us to analyze fluid interactions effectively.
-
Gradient Lines: Energy and hydraulic gradient lines aid in visualizing energy transformations in fluid flow.
-
Coefficient of Discharge: C_d quantifies the difference between the actual discharge and theoretical values in fluid flow devices.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The fuel efficiency improvements in car designs due to aerodynamic shapes, lowering the drag coefficient from 0.8 to 0.15.
-
Using an orifice meter to measure fluid flow, considering energy losses dictated by the coefficient of discharge.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluids we flow, Bernoulli's our guide, / For pressure and speed, let energy ride!
📖 Fascinating Stories
-
Imagine a race car navigating curves — it uses shape (drag coefficient) to minimize wind resistance and maximize speed, much like how Bernoulli’s Equation optimizes fluid flow.
🧠 Other Memory Gems
-
Use 'PSP' to remember: Pressure, Static, and Potential for pressures in fluid dynamics.
🎯 Super Acronyms
Remember 'CDE' for
- Coefficient
- Discharge
- and Errors in measuring flow performance.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Bernoulli Equation
Definition:
An equation that relates pressure, velocity, and gravitational potential energy in fluid flow.
-
Term: Static Pressure
Definition:
The pressure exerted by a fluid at rest.
-
Term: Dynamic Pressure
Definition:
The pressure associated with the fluid's motion.
-
Term: Stagnation Pressure
Definition:
The pressure experienced by a fluid when it is brought to a complete stop.
-
Term: Energy Gradient Line
Definition:
A line representing the total energy head of the fluid flow along a streamline.
-
Term: Hydraulic Gradient Line
Definition:
A line representing the static pressure head and elevation head of the fluid flow along a streamline.
-
Term: Coefficient of Discharge (C_d)
Definition:
A dimensionless number used to compare the actual discharge to theoretical discharge in fluid flow systems.