Hydraulic and Energy Gradient Lines
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Gradient Lines
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will learn about hydraulic and energy gradient lines. Who can tell me what you think these lines represent in fluid mechanics?

Do they indicate how pressure changes in a fluid?

That's a good start! The hydraulic gradient line represents the height of the static pressure head. It indicates the pressure changes in the fluid along a pipe or channel.

And what about the energy gradient line?

Great question! The energy gradient line includes pressure, kinetic, and potential energy heads. It shows how the total energy of the fluid changes along the flow.

Why is it important to understand these lines?

Understanding these lines allows us to assess energy losses in flow systems, which is crucial for designing efficient hydraulic systems. Remember, energy flows from higher to lower gradients.

So, does that mean if the energy gradient line is flat, there won’t be any flow?

Exactly! A flat energy gradient line indicates no pressure difference to drive the flow. Let's summarize: the HGL measures static pressure, and the EGL measures total energy head across a flow field.
Applications of Gradient Lines
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've covered what the gradient lines are, can anyone think of how we might apply this in a practical context?

I think they are used in designing pipe systems to predict flow behavior.

Absolutely! Engineers use these lines to analyze how fluids flow through pipes and channels, assessing energy losses due to friction and turbulence.

Can we visualize this? How do we draw these lines?

Good point! To visualize the HGL, draw it based on static pressures measured at different points in a pipe. The EGL can be drawn above the HGL, including the velocity head.

What happens when we have pumps in the system?

Pumps will raise the energy gradient line, allowing us to see how much energy is being added to the system, which is crucial for proper design.

So knowing where the HGL and EGL are helps us prevent issues like cavitation?

Exactly! Understanding hydraulic and energy gradient lines helps avoid cavitation by ensuring we maintain enough pressure in the system.
Energy Changes and Losses
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s delve deeper into energy changes. What do you think influences energy losses in a system?

Could it be due to friction or turbulence?

Yes! Friction and turbulence within the fluid flow significantly influence energy losses, which we need to consider in our calculations.

How do we account for that in our calculations?

We introduce a coefficient of discharge to relate actual discharge to theoretical discharge, considering these losses.

So, the coefficient of discharge helps us adjust for energy losses?

Exactly! It’s a vital concept in ensuring our designs are accurate and efficient.

Relating the EGL and HGL is essential, right? What if one is higher than the other?

Correct! If the EGL is consistently above the HGL, it signifies a functioning system. If the HGL rises above the EGL, it indicates a potential for cavitation or air entrainment in the system.

In conclusion, understanding the relationship between energy losses and the respective gradient lines is crucial for optimal fluid mechanics design.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section elaborates on the significance of hydraulic and energy gradient lines as practical applications of the Bernoulli equation, highlighting their roles in analyzing energy changes in fluid systems.
Detailed
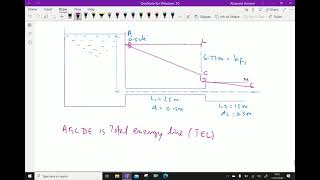
Hydraulic and Energy Gradient Lines
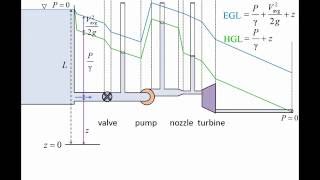
This section explores the concepts of hydraulic and energy gradient lines within the framework of the Bernoulli equation, a cornerstone of fluid dynamics. The Bernoulli equation relates the pressure, velocity, and elevation of a fluid flowing along a streamline, establishing a conservation of energy principle for fluids. The hydraulic gradient line (HGL) represents the height of the static pressure head, while the energy gradient line (EGL) depicts the total mechanical energy head (including kinetic and potential energies) of the fluid.
The interplay between these lines elucidates how energy is distributed and dissipated in various fluid scenarios, such as pipe flow systems or open channels. The energy gradient line reflects changes in energy due to pressure, velocity, and elevation head, essential for practical applications like designing hydraulic systems. Overall, understanding these gradients enables engineers to quantify energy losses and optimize fluid transport systems.
Youtube Videos

![Hydraulic and Energy Grade Line ? with animation [ HGL and EGL ]](https://img.youtube.com/vi/moI4DQNirAw/mqdefault.jpg)



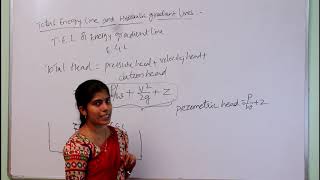


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Concept of Energy Gradient Line
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Energy gradient line represents the total head of the fluid, comprising flow energy, kinetic energy, and potential energy along a streamline.
Detailed Explanation
The energy gradient line (EGL) is a visual representation of the total energy present in a fluid flow system at various points. It combines three forms of energy: the kinetic energy due to fluid motion, the potential energy due to the height of the fluid, and the pressure energy due to the fluid’s static pressure. The comparison of how these energies shift illustrates how they influence flow behavior through pipes or channels.
Examples & Analogies
Imagine a river flowing downhill. At the top of a hill, the water has high potential energy (it's elevated). As the river flows down, part of this potential energy transforms into kinetic energy (speed). On a graph, the height of the river would drop, showing the energy gradient line decreasing as the speed of the flowing water increases.
Hydraulic Gradient Line
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The hydraulic gradient line (HGL) shows the static pressure head and elevation head but does not include velocity head.
Detailed Explanation
While the energy gradient line (EGL) includes all forms of energy, the hydraulic gradient line (HGL) focuses solely on the static and elevation heads in a fluid system. This means it only accounts for the pressure energy and the potential energy from height, which are important for determining the pressure of the fluid throughout its path. The HGL indicates where pressure forces can supply flow and where pressures may drop below certain thresholds.
Examples & Analogies
Consider a water tank. The height of the water in the tank is analogous to the static head or HGL, giving an idea of how much pressure is available to push water out of a tap. When you open the tap, the water flows because there’s enough pressure from the height of water above. The difference in height directly impacts the pressure available at the tap.
Flow Direction Related to Energy Levels
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Fluid flows from higher energy levels to lower energy levels.
Detailed Explanation
Fluid movement generally occurs from regions of higher energy to those of lower energy. This principle helps explain why water flows downhill; it’s moving place to place where the total energy is less. Understanding the energy gradient helps engineers design systems that can ensure efficient flow without unwanted blockages or surges.
Examples & Analogies
Think of air moving from a high-pressure area to a low-pressure area, such as opening a bottle of soda. The carbonated bubbles rush out quickly when the pressure is released, demonstrating fluid moving from higher energy levels (inside the bottle) to lower energy levels (outside), just like a waterfall flows from a high cliff to a lower river.
Measuring Gradient Lines
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The energy gradient line and hydraulic gradient line can be measured using devices such as piezometers and pitot tubes.
Detailed Explanation
Engineers use devices called piezometers and pitot tubes to measure the different pressures in fluid systems. A piezometer measures static pressure, while a pitot tube measures dynamic pressure. By employing these instruments, engineers can quantify how energy varies in a flow and establish hydraulic and energy gradient lines that visualize this information. This is critical for making accurate predictions about how a system will behave under various conditions.
Examples & Analogies
Imagine checking the height of water in different tanks using rulers (piezometers) and seeing how quickly water spills from one to another using a funnel (pitot tube). The height indicates pressure at each level, while the rate of spill shows how fast it can flow based on pressure differences—essentially, a practical way to measure and visualize energy and pressure in a fluid system.
Key Concepts
-
Hydraulic Gradient Line: Represents the static pressure head of the fluid.
-
Energy Gradient Line: Depicts the total mechanical energy of the fluid flow.
-
Bernoulli Equation: Governs the relation between pressure, velocity, and elevation.
-
Coefficient of Discharge: Represents the ratio of actual to theoretical discharge accounting for energy losses.
-
Understanding Cavitation: Reflects the importance of maintaining pressure levels to prevent vapor bubble formation in fluid.
Examples & Applications
In a curved pipe, if the energy gradient line drops significantly at a bend, it indicates energy loss due to turbulence and friction, which could impact flow efficiency.
By assessing the hydraulic gradient line, engineers can determine the required pump height to ensure adequate system pressure.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In pipes and flows, where pressure does glow, the static head rises, while energy flows slow.
Stories
Imagine a river flowing down a hill; as it descends, the height drops, but energy is always conserved in the flow, representing gradient lines.
Memory Tools
E-Gas for EGL (Energy Gradient Line) - Energy, Gravity, and Static pressure.
Acronyms
HGL - Hydraulic Gradient Line
Think Hard to Gauge Liquids!
Flash Cards
Glossary
- Hydraulic Gradient Line (HGL)
A line that represents the static pressure head in fluid flow.
- Energy Gradient Line (EGL)
A line that indicates the total mechanical energy head of a fluid, including pressure, kinetic, and potential energy.
- Bernoulli Equation
An equation that relates the velocity, pressure, and elevation of a fluid moving along a streamline.
- Coefficient of Discharge (C)
A dimensionless number that relates the actual discharge to the theoretical discharge in a fluid flow system, accounting for energy losses.
- Cavitation
The formation and collapse of vapor bubbles in a fluid, typically due to sudden changes in pressure.
Reference links
Supplementary resources to enhance your learning experience.
