Energy Gradient Line
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Bernoulli Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll explore the Bernoulli equation and its significance in fluid mechanics. Can anyone share what they know about it?

I know that it simplifies fluid flow problems!

Correct! It has revolutionized designs in pipe and channel flows since it was introduced in the 18th century. Remember, Bernoulli’s equation relates pressure, kinetic energy, and potential energy of flowing fluids. Who can tell me why these relationships are important?

They help to understand how energy changes in fluid systems!

Exactly! Let's also remember the acronym 'PEEK' to keep in mind the three main components of energy in fluids: Pressure, Kinetic Energy, and Elevation. Now, let’s proceed to the energy gradient.
Energy Gradient and Hydraulic Gradient Lines
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Can anyone tell me the difference between the energy gradient line and the hydraulic gradient line?

The energy gradient line includes all forms of energy, while the hydraulic gradient line only considers pressure and elevation.

Great observation! The energy gradient line represents the total energy, while the hydraulic gradient line tells us about pressure head and elevation head. Remember, the flow moves from higher energy to lower energy. How might we visualize this?

We could draw both lines on a diagram of a flowing river!

Exactly! Visual aids help cement our understanding. Let’s conclude this session with the takeaway: 'Flow follows energy'.
Pressure Components in Fluid Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s talk about the types of pressure in fluids. Who can define static pressure?

Static pressure is the pressure exerted by a fluid at rest at a point in the system.

Exactly! And dynamic pressure? How does it differ?

Dynamic pressure is the pressure due to fluid motion measured as �(1/2 � pv^2). It represents kinetic energy.

Right! And stagnation pressure is a combination of both. Critically think about how understanding these pressures can be applied in real scenarios. Can anyone give an example?

Yeah! In aerodynamics, we measure stagnation pressure to determine airspeed over an aircraft.

Exactly! This concept is crucial for engineers in various fields. Let's encapsulate this with the mnemonic 'PDS' for Pressure, Dynamic, Stagnation.
Kinetic Energy Correction Factors
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Who can explain why we need kinetic energy correction factors when dealing with non-uniform flow?

Because flows can have uneven distributions, using an average velocity can lead to incorrect energy calculations.

Exactly! In most cases, flows deviate from uniformity, necessitating the use of correction factors, denoted as �(α). What do we typically use for laminar flow?

For laminar flow, we can approximate α as 2.

Correct! In turbulent flow, it can vary from 1.04 to 1.1. Remember, 'Kinetic equals Correction.' This ties in closely with our earlier discussions of energy!
Applications of Hydraulic and Energy Gradient Lines
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s explore real-world applications of our concepts today. When we design pipelines, why is understanding energy gradient lines crucial?

It helps to predict energy losses, and therefore, design the system for efficiency and safety.

Perfect! What about open channel flows? How do these concepts apply there?

We can use Bernoulli’s equations to compute energy losses and flow rates, and accurately gauge performance.

Fantastic responses! Our discussion underscores how theoretical concepts translate into practical engineering solutions. Remember the term 'Flow Measurement' for future reference!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section explores the significance of the Energy Gradient Line and Hydraulic Gradient Line in fluid mechanics. It explains how fluid energy is quantified and the relationship between static, dynamic, and stagnation pressures, with applications in real-world systems such as pipes and channels.
Detailed
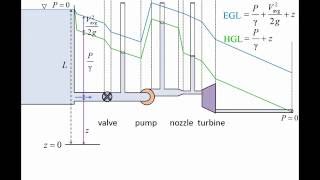
Energy Gradient Line
The Energy Gradient Line is a pivotal concept in fluid mechanics that leverages the principles laid out by the Bernoulli equation. This section delves into the relationship between fluid flow, energy conservation, and velocity distributions in various systems. The key aspects discussed include:
- Bernoulli Equation Overview: A brief history and significance of the Bernoulli equation in solving fluid flow problems.
- Hydraulic and Energy Gradient Lines: Explanation of what these lines are, how they are derived, and the importance of measuring pressures within fluid systems.
- Pressure Components: Understanding static, dynamic, and stagnation pressures, and how they contribute to the overall energy of a fluid throughout its motion.
- Flow Dynamics: The process of fluid flow from high energy to low energy zones and the energy losses that occur in real systems, leading to calculations using coefficients of discharge.
- Kinetic Energy Correction Factors: Addressing the non-uniform distributions of flow, highlighting how average velocities require corrections in kinetic energy calculations.
- Practical Applications: Real-world implications, including examples of pipes, channels, and instrumentation for measuring fluid parameters.
The Energy Gradient Line concept proves essential for engineers, aiding in the prediction and analysis of fluid behaviors critical for effective design and operation in civil and mechanical engineering applications.
Youtube Videos

![Hydraulic and Energy Grade Line ? with animation [ HGL and EGL ]](https://img.youtube.com/vi/moI4DQNirAw/mqdefault.jpg)







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Energy Gradient Line
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The basic concept here is called that we should always gauge energy gradient line, hydraulic gradient line. So, any flow patterns, we have to draw the energy gradient line and hydraulic gradient line.
Detailed Explanation
The energy gradient line (EGL) represents the total energy in a fluid system along a streamline. This includes the potential energy due to elevation, kinetic energy due to fluid velocity, and flow energy due to pressure. The hydraulic gradient line (HGL), on the other hand, considers only the pressure head and elevation head without accounting for kinetic energy. Thus, the EGL will always be higher than the HGL in flowing conditions because it contains additional kinetic energy measurements as well.
Examples & Analogies
Imagine a water slide. The energy gradient line can be likened to the height of the slide, which dictates how fast you will go down. The hydraulic gradient line, while lower, represents the water level in the slide, showing the pressure the water exerts but not taking into account the speed of the slide at any point.
Flow Direction and Energy Loss
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Fluid flows from higher energy to lower energy, not the higher elevation to lower elevation. Please do not have that things. The fluid flows from higher energy to lower energy.
Detailed Explanation
This point emphasizes that fluid movement is driven by energy differences, not just differences in height. This means that a region of high energy (combining pressure, velocity, and elevation) will have fluid flowing to a region of lower energy. When fluid flows from high energy to low energy, energy losses can occur due to friction, turbulence, and other disruptions in the flow.
Examples & Analogies
Think of a steep hill with a stream flowing down it. While the height of the hill is important, what's truly driving the water down the hill is the gravitational energy (or potential energy) translating into kinetic energy as it flows. If the stream encounters obstacles like rocks or becomes narrower, it will lose energy due to turbulence, much like how a car might slow down if it hits bumps or sharp turns.
Hydraulic Gradient Line Measurement
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The hydraulic gradient line has some of the static pressures and the elevations. And the vertical distance above the pipe center is measure of the pressure within the pipe.
Detailed Explanation
The hydraulic gradient line (HGL) provides a visual representation of the potential energy available to the fluid due to its elevation and pressure alone. It can be calculated by adding the static pressure (P/g) with the elevation head (z), where P is the pressure within the pipe and g is the gravitational constant. This is important for understanding how pressure is distributed along the flow and helps in assessing the potential energy at various points in the system.
Examples & Analogies
Imagine a water tower that supplies water to a neighborhood. The height of the tower gives it potential energy. If you measure how high the water level is in the tower (potential energy) and combine that with the pressure the water is under (static pressure), you can calculate the forces at play within the pipes leading to homes. This helps engineers ensure there's adequate pressure for every household.
Flow Energy Contribution
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Whenever flow from higher energy to lower energy, definitely there is an energy loss happens.
Detailed Explanation
As fluid transitions from higher to lower energy zones, it undergoes energy losses primarily due to friction between the fluid and the pipe's interior surface, turbulence, and other flow disruptions. This is often quantified in engineering applications to understand how much energy is being lost in a system, which can impact the efficiency of designs for pumps, turbines, and other fluid transport systems.
Examples & Analogies
Consider riding a bicycle uphill versus downhill. Going uphill requires more energy and effort (higher energy) compared to coasting downhill where gravity assists you but you might lose some speed due to friction with the bike’s tires and wind resistance—similar to how energy is lost when water flows through a pipe.
Drawing Energy Gradient and Hydraulic Gradient Lines
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Whenever we design the pipe flow or channel flow and all, we need to draw energy gradient line and the hydraulic gradient line.
Detailed Explanation
When designing systems like pipelines or open channels, plotting the energy gradient line and hydraulic gradient line is crucial for predicting behavior, assessing potential flow rates, and determining pressure drops. By visualizing these lines, engineers can make informed decisions about how to adjust their systems for optimal flow and minimal energy loss.
Examples & Analogies
Imagine you're designing a water park with a lazy river. To ensure that the water flows smoothly, you would need to draw out where the water will flow quickest (energy gradient line) and where it might slow down due to obstacles or curves (hydraulic gradient line). This helps you create an enjoyable experience without unexpected stops or leaks.
Key Concepts
-
Bernoulli Equation: A foundational equation in fluid dynamics that relates pressure, velocity, and height.
-
Energy Gradient Line: Represents total energy in a fluid system along a streamline, crucial for analyzing flow.
-
Hydraulic Gradient Line: Indicates pressure head and elevation in a fluid system, important for understanding pressure dynamics.
-
Kinetic Energy Correction Factor: Adjusts calculations of kinetic energy for flows that are not uniform.
Examples & Applications
Example 1: The use of the Bernoulli equation in comparing the speeds of a fluid at different heights in a pipe.
Example 2: Calculating stagnation pressure using a pitot tube in an aircraft to determine airspeed.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Flowing fluid through a pipe, energy levels take a hike. From high to low, they'll drift and slide, energy gradient takes you for a ride.
Stories
Imagine a river flowing down a mountain. As it tumbles over rocks, it loses energy, illustrating the journey from high energy to low. It's my energy gradient line story, leading to understanding fluid flows.
Memory Tools
Remember 'PEEK' to keep in mind: Pressure, Energy, Elevation, Kinetic in fluid design.
Acronyms
Use 'HED' for Hydraulic Energy Dynamics
Hydraulic element for pressure
Elevation head for height
and D for dynamic pressure.
Flash Cards
Glossary
- Bernoulli Equation
A principle in fluid dynamics that describes the conservation of energy in flowing fluids.
- Energy Gradient Line
A line that represents the total mechanical energy of a fluid along a streamline.
- Hydraulic Gradient Line
A line that indicates pressure and elevation heads in a fluid flow system, excluding kinetic energy.
- Static Pressure
The pressure exerted by a stationary fluid within a system.
- Dynamic Pressure
The pressure associated with the motion of the fluid, calculated as 1/2 ρv².
- Stagnation Pressure
The pressure experienced by a fluid when it is brought to rest, combining static and dynamic pressures.
- Kinetic Energy Correction Factor (α)
A multiplier used to correct kinetic energy calculations based on flow uniformity.
Reference links
Supplementary resources to enhance your learning experience.
