Static Pressure
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Static Pressure
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning, class! Today we’ll explore static pressure. Can anyone tell me what static pressure is?

Is it the pressure exerted by a fluid that is at rest?

Exactly! Static pressure measures the force exerted by a fluid when it is not moving. It’s a crucial aspect in understanding fluids in equilibrium.

How does it differ from dynamic pressure?

Good question! Unlike static pressure, dynamic pressure relates to the motion of the fluid. The relationship among static, dynamic, and stagnation pressures is fundamental in fluid mechanics. Remember: Static + Dynamic = Stagnation.

Can we relate static pressure to Bernoulli's equation?

Yes! Bernoulli's equation incorporates static pressure as a key term representing the energy balance in flowing fluids. We’ll delve deeper into that concept shortly.

In summary, static pressure is essential for understanding fluid behavior and lays the groundwork for more complex concepts in fluid mechanics.
Dynamic and Stagnation Pressure
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've covered static pressure, let’s move on to dynamic pressure. What do you understand by dynamic pressure?

Is it the pressure from fluid movement?

Exactly! Dynamic pressure is given by the formula 0.5 * ρ * v², where ρ is density and v is velocity. It reflects the kinetic energy of the fluid’s motion.

And stagnation pressure, how does it fit in?

Great connection! Stagnation pressure is what you get when you bring a fluid to rest—it's the sum of static and dynamic pressures. So, stagnation pressure indicates total energy at that point.

Can we see examples where stagnation pressure is used?

Certainly! Pitot tubes used in aircraft measure stagnation pressure to determine airspeed effectively. They harness the relationship between these pressures beautifully.

To summarize, dynamic pressure tells us about the energy of fluid in motion, while stagnation pressure helps us assess total energy by considering both static and dynamic components.
Applications of Pressure Types
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

We’ve learned individual concepts; now let’s look at their applications! Why is understanding these pressures important in engineering?

It helps us design systems like pipelines or aircraft!

Precisely! Engineers use these pressures to design efficient systems that account for energy conservation, like in pipe flow calculations or aerodynamic designs.

What are common mistakes in measuring these pressures?

A common mistake is neglecting the energy loss due to friction or turbulence, which can lead to inaccuracies in calculations. Always remember to apply correction factors!

How do we calculate these pressures in real situations?

We apply Bernoulli's equation in systems under ideal conditions to relate the pressures. Remember: pressure measurements should also consider practical applications and corrections.

In conclusion, understanding and correctly applying static, dynamic, and stagnation pressure allows us to harness the theory of fluid mechanics effectively in practical scenarios.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Static pressure is an essential concept in fluid mechanics that defines the pressure exerted by a fluid at rest. This section further investigates three pressure types: static, dynamic, and stagnation pressures, explaining their significance in Bernoulli's equation and the principles governing fluid dynamics.
Detailed
Static Pressure in Fluid Mechanics
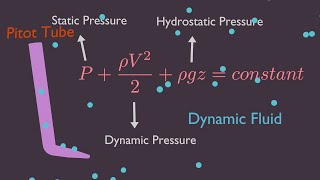
Static pressure is a critical concept in fluid mechanics, defined as the pressure exerted by a fluid at rest. Alongside dynamic and stagnation pressures, it forms the foundation of the Bernoulli equation, which describes the conservation of energy in a moving fluid. The Bernoulli equation represents the relationship between these three pressures—in which static pressure is the hydrostatic pressure, dynamic pressure is the pressure due to fluid motion, and stagnation pressure is the sum of static and dynamic pressures at a point where fluid is brought to a complete stop.
Understanding these pressures is vital for various applications in fluid flow systems, including pipe flow, ventilation, and hydraulic design. By analyzing static pressure and other related pressures, engineers can predict how fluids behave under different conditions and apply this understanding effectively to real-world problems.
Youtube Videos





![Static Pressure: Example 1 [Fluid Mechanics #9]](https://img.youtube.com/vi/CX96H3xRhV4/mqdefault.jpg)



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Static Pressure
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Static pressure is the pressure exerted by a fluid at rest and can be measured using devices like piezometers.
Detailed Explanation
Static pressure refers to the force exerted by a fluid when it is not moving. It is the pressure felt by an object submerged in that fluid. For instance, when measuring static pressure in a pipe, the fluid's weight and any external forces determine how much pressure is exerted at that point. Commonly, static pressure is measured using piezometers, which are small tubes that display fluid height relative to atmospheric pressure.
Examples & Analogies
Imagine you’re at the bottom of a swimming pool. You can feel the water pushing down on you. This pressure you feel is static pressure. The deeper you go, the more pressure there is because of the weight of the water above you.
Dynamic Pressure and Stagnation Pressure
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Dynamic pressure is the pressure due to the fluid's velocity. It combines with static pressure to form stagnation pressure, which occurs when fluid flows are brought to a complete stop.
Detailed Explanation
Dynamic pressure depends on the movement of the fluid and can be calculated using the formula: \( q = \frac{1}{2} \rho V^2 \), where \( \rho \) is the fluid density and \( V \) is the velocity. When fluid encounters a barrier and comes to a standstill, the static pressure is increased by the dynamic pressure; this sum is known as stagnation pressure. Stagnation pressure is critical in various applications, including aircraft design, where it is utilized to determine airspeed.
Examples & Analogies
Think of dynamic pressure as the speed of a car. When you’re driving fast, your car creates a lot of air pressure in front of it. If you drive into a wall (the barrier), all that speed (dynamic pressure) is converted into a buildup of pressure at the point of impact, similar to how stagnation pressure works.
Pressure Measurement Techniques
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
To measure static and dynamic pressures simultaneously, a Pitot tube can be used. It helps determine both types of pressure in fluid flows.
Detailed Explanation
A Pitot tube measures the stagnation pressure by capturing the fluid flow directly inside the tube. The pressure created by the fluid bringing it to a stop (stagnation pressure) is measured against ambient pressure. By knowing the static pressure (via another measurement, like from a piezometer), we can easily calculate the dynamic pressure and, consequently, the fluid's velocity using Bernoulli's equation.
Examples & Analogies
Consider the way a straw works when you sip a drink. When you create a vacuum by sucking on the straw (akin to applying dynamic pressure), you can measure how much drink is pulled into the straw. Similarly, a Pitot tube measures how much of the fluid stops upon hitting it, allowing us to understand both the static and dynamic pressures.
The Importance of Static Pressure in Fluid Flow
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In various engineering applications, static pressure plays a vital role in determining fluid behavior in systems, such as pipelines and open channels.
Detailed Explanation
Static pressure is crucial in determining how fluids behave in various systems. For example, in pipelines, it influences how pressure changes occur along the pipe length. Understanding static pressure can help engineers design systems that effectively manage fluid distribution without causing damage or leaks. In open channels, it affects flow patterns and velocity distributions.
Examples & Analogies
Think of a garden hose connected to a tap. If you open the tap slightly, static pressure in the hose will determine how much water flows out. If you block the end of the hose, static pressure will build up, showing you how critical it is to maintain the right pressure to ensure proper water flow.
Key Concepts
-
Static Pressure: Pressure exerted by a fluid in a state of rest.
-
Dynamic Pressure: Pressure related to the motion of the fluid, indicating kinetic energy.
-
Stagnation Pressure: Sum of static and dynamic pressure when a fluid is brought to rest.
Examples & Applications
Example of static pressure: The pressure at the bottom of a water tank is higher due to the weight of the water above it, illustrating static pressure.
Example of using Bernoulli’s equation: Engineers use this equation to compute flow rates in water systems, relating heights, and pressures in pipes.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Static pressure holds the ground, while dynamic pressure spins around.
Stories
Imagine a calm lake representing static pressure, while a flowing river demonstrates dynamic pressure. The river joins the lake, creating stagnation where motion stops.
Memory Tools
SDS: Static - Dynamic - Stagnation - remember their order in fluid dynamics.
Acronyms
PDC
Pressure
Dynamics
Conservation - keep these in mind while using Bernoulli's equation.
Flash Cards
Glossary
- Static Pressure
The pressure exerted by a fluid at rest, measured perpendicular to the surface.
- Dynamic Pressure
The pressure associated with the fluid's motion, calculated as 0.5 * ρ * v².
- Stagnation Pressure
The pressure at a point where the fluid is brought to a complete stop, which is the sum of static and dynamic pressures.
- Bernoulli Equation
An equation that describes the conservation of energy for an incompressible fluid flow along a streamline.
Reference links
Supplementary resources to enhance your learning experience.
