Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Orifice Meters
Unlock Audio Lesson
Today, we're focusing on orifice meters. These devices measure fluid flow by assessing the pressure difference across a hole in a plate. Can anyone tell me why this pressure difference matters?
I think it helps us know how fast the fluid is moving.
Exactly! The pressure difference enables us to apply Bernoulli's equation and calculate the flow rate. Remember, this basic principle is foundational for understanding fluid mechanics.
What are some applications of orifice meters?
Great question! Orifice meters are used in various industries, from water management to oil refineries. They provide an essential measurement of fluid discharge.
Let's summarize: Orifice meters measure fluid flow based on pressure differences, and their applications span across several industries.
Energy Losses in Fluid Flow
Unlock Audio Lesson
As we delve deeper, we must understand that energy losses, such as friction and turbulence, play a pivotal role in the flow through orifice meters. Who can tell me why we must consider these losses?
Because they can cause the actual discharge to be less than the theoretical discharge, right?
Exactly! The coefficient of discharge, or Cd, helps us quantify this difference. It’s the ratio of actual discharge to theoretical discharge. Can anyone provide a situation where this would be useful?
In pipelines, if we know the losses, we can better predict the flow rates and manage resources efficiently.
Perfect example! Understanding energies and losses is crucial for accurate flow calculations in those situations.
Kinetic Energy Correction Factors
Unlock Audio Lesson
Let's examine kinetic energy correction factors. When fluid flows through pipes, the velocity isn't uniform. Can anyone think of a reason this matters when calculating kinetic energy?
If we only use average velocities, we might miscalculate the energy?
Correct! That's why we factor in a correction factor, denoted as α (alpha), which adjusts our calculations for different types of flows.
What’s an example of these factors in terms of flow types?
For fully developed laminar flow, α can be approximately 2, while turbulent flow ranges from 1.04 to 1.1. This adjustment is crucial for precise energy calculations.
In summary, kinetic energy correction factors account for velocity distribution and refine our energy calculations.
Pressure Definitions: Static, Dynamic, and Stagnation
Unlock Audio Lesson
Next, we must understand the pressures involved: static, dynamic, and stagnation pressures. Who can describe what static pressure means?
It's the pressure exerted by a fluid at rest?
Correct! And dynamic pressure arises from fluid motion. Can someone define stagnation pressure?
That's when the fluid is brought to a stop, right?
Exactly! Stagnation pressure is the sum of static and dynamic pressures. Knowing how these pressures interact helps us predict fluid behavior accurately.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the operational principles of orifice meters, contrasting them with venturimeters. Key concepts include the importance of kinetic energy correction factors and the coefficient of discharge, which account for discrepancies between theoretical and actual fluid flow measurements due to energy losses.
Detailed
Orifice Meter Functionality
The orifice meter is a device used to measure the flow rate of a fluid, commonly employed in various engineering applications. This section discusses the fundamental principles governing its operation and highlights significant factors influencing flow measurement accuracy.
Key Topics:
- Definition of Orifice Meter: The orifice meter consists of a thin plate with a hole (orifice) through which the fluid passes. Unlike venturimeters, which have varying cross-sectional zones, the orifice meter maintains a simple design, measuring pressure differences between inflow and outflow sides.
- Bernoulli's Equation Application: Utilizing Bernoulli's equation alongside mass conservation principles allows for calculating the theoretical discharge. However, real-life applications reveal discrepancies between theoretical calculations and actual discharge due to energy losses from friction, turbulence, and vortex formations.
- Coefficient of Discharge (Cd): To reconcile these discrepancies, engineers introduce the coefficient of discharge, representing the ratio of actual discharge to the theoretical discharge. This coefficient is crucial for accurate flow calculations.
- Kinetic Energy Correction Factors: Due to non-uniform velocity distributions within the pipe, kinetic energy correction factors are employed to adjust calculations of kinetic energy based on average velocity. This adjustment ensures more accurate flow assessments.
- Pressure Definitions: The section also covers static, dynamic, and stagnation pressures, which are vital for understanding fluid behavior in various scenarios.
In summary, this section emphasizes the necessity of accounting for energy losses in fluid flow measurements and the role of orifice meters in engineering practices.
Youtube Videos
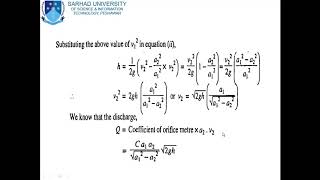
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Orifice Meters
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now come back to the where simple experimental setups, we generally do the measuring the flow in a pipe, either in a venturimeter or the orifice meter. The orifice meter is a smalle device, that means it will be a circle and there is a hole inside this. This is called the orifice.
Detailed Explanation
Orifice meters are devices used to measure the flow of fluids through pipes. They consist of a flat plate with a hole known as the 'orifice'. When fluid passes through this hole, it creates a drop in pressure due to the constriction, which can be measured to determine the flow rate. This setup is simpler than that of a venturimeter, which includes both converging and diverging sections.
Examples & Analogies
Think of an orifice meter like a small door in a larger wall. When you open this door, the flow of people (or in this case, fluid) is restricted, causing a buildup of crowding on one side and a rush of people through the door. The more people (or fluid) trying to pass through the door, the more noticeable the effect on the crowding and flow becomes.
Pressure Difference in Orifice Meters
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We can measure the pressure difference at two locations; one is at the fiber locations where the cross section is less and another is the off stream locations.
Detailed Explanation
In an orifice meter, pressure is measured at two distinct points: one at the orifice (where the cross-section of flow is smallest) and another downstream. The difference in pressure between these two locations is directly related to the flow rate of the fluid. According to Bernoulli's principle, a reduction in area (such as the area at the orifice) results in an increase in fluid velocity and a corresponding drop in pressure.
Examples & Analogies
Imagine using a garden hose with your thumb partially blocking the end. When you pinch the end, the water sprays out with higher speed, but the pressure where your thumb is applied (the orifice) drops. This principle is similar to how an orifice meter measures flow.
Energy Losses in Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But as I said it earlier, whenever flow goes through these venturimeter or orifice meter, there will be energy losses. Because of the energy losses, they will be difference between theoretical discharge and actual discharge.
Detailed Explanation
While orifice meters provide a way to calculate fluid flow based on pressure differences, energy is often lost due to friction and turbulence within the fluid as it passes through the orifice. These losses can cause the actual flow rate (actual discharge) to be less than the flow rate predicted by theoretical calculations (theoretical discharge). It’s important to account for these losses to achieve accurate measurements.
Examples & Analogies
Consider driving a car downhill. The speed you can theoretically achieve (theoretical discharge) is not what happens in practice due to factors like wind resistance and road friction (energy losses). Similarly, in fluid flow, certain energy is lost, causing the flow rate to be lower than expectations.
Coefficient of Discharge (CD)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Since the Bernoulli equations what we applied, we do not consider the energy loss components. We consider there is no energy losses, okay. No the frictional resistance is more or there is no vortex formations and all. But in the real fluid flow, there is energy losses. Because of that, what do you will have, your theoretical discharge compute from the Bernoulli equations and the mass conservations will be more than actual discharge. So actual discharge, the difference between these, we introduce a coefficient of discharge, that means the CD.
Detailed Explanation
In fluid mechanics, the coefficient of discharge (CD) is introduced to quantify the relationship between the theoretical discharge and the actual discharge in an orifice meter. It accounts for the energy losses that occur during the flow through the orifice. The CD indicates how much of the theoretical flow is actually achieved in practice, serving as a corrective factor to improve measurement accuracy.
Examples & Analogies
Think of a sponge soaking up water. If a sponge can theoretically hold a certain amount of water, but in practice, it loses some due to leaks or less-than-perfect absorption, the 'actual amount' absorbed would be lower than expected. The coefficient of discharge in an orifice meter works in the same way, correcting the discrepancy between theoretical and actual flow rates.
Importance of Kinetic Energy Correction Factors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, when you apply the kinetic energy, we look at the total kinetic energy, which is we can integrate over that a small dA element with a. This is a mass flux, rho V dot n is a mass flux and this is a half rho V square is the mass flux into V square by 2 is a kinetic energy flux.
Detailed Explanation
To accurately understand fluid flow and apply the Bernoulli equation, we must consider kinetic energy correction factors due to variations in flow speed within the pipe. The flow doesn't move uniformly, leading to challenges in calculating accurate kinetic energy. Integrating kinetic energy across the flow area allows for a more realistic assessment, which leads to the application of correction factors in practical calculations.
Examples & Analogies
Imagine riding a bicycle through a park where the path isn't straight, and the speed varies depending on your effort. If you want to know your average speed for the entire ride, you can't simply take your maximum speed; you need to consider where you slowed down or sped up. Similarly, in fluid dynamics, we account for the variations in speed to correctly calculate kinetic energy.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Orifice meters measure fluid flow based on pressure differences.
-
Bernoulli's equation is essential for calculating theoretical discharge.
-
Coefficient of discharge helps account for energy losses.
-
Kinetic energy correction factors adjust for non-uniform velocity distributions.
-
Static, dynamic, and stagnation pressures are critical for understanding fluid behavior.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An orifice meter is regularly used in water treatment plants to measure flow rates of incoming water.
-
In a pipeline transporting oil, the coefficient of discharge is calculated to ensure efficient operation despite energy losses.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If flow's not fair and pressure's a mess, the discharge coefficient helps us assess!
📖 Fascinating Stories
-
Once upon a time in a fluid kingdom, an orifice meter helped the wise king measure the flow of rivers, ensuring the right amount of water was dispensed to his land.
🧠 Other Memory Gems
-
Remember 'SPA': Static, Dynamic, and Stagnation pressures to recall the types of pressures in fluid dynamics.
🎯 Super Acronyms
For understanding orifice functionality, use 'FLOWS'
- Flow measurement
- Losses accounted
- Orifice design
- Water management
- Simplified calculations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Orifice Meter
Definition:
A device used to measure fluid flow by creating a pressure difference across a hole in a plate.
-
Term: Bernoulli's Equation
Definition:
An equation relating pressure, velocity, and height for incompressible fluids along a streamline.
-
Term: Coefficient of Discharge (Cd)
Definition:
A dimensionless number representing the ratio of actual discharge to theoretical discharge.
-
Term: Kinetic Energy Correction Factor (α)
Definition:
A factor used to adjust kinetic energy calculations when velocity distributions within a pipe are non-uniform.
-
Term: Static Pressure
Definition:
The pressure exerted by a fluid at rest.
-
Term: Dynamic Pressure
Definition:
The pressure associated with the fluid's motion, proportional to the square of the velocity.
-
Term: Stagnation Pressure
Definition:
The pressure measured when a fluid is brought to a complete stop, equal to static pressure plus dynamic pressure.