Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Pressures in Fluid Mechanics
Unlock Audio Lesson
Welcome, everyone! Let's dive into the essential types of pressures in fluid mechanics. Can anyone tell me what static pressure is?
Is it the pressure at a point when the fluid is at rest?
Exactly! Static pressure is the pressure exerted by a fluid at rest. Now, how about dynamic pressure?
Is dynamic pressure related to the fluid's velocity?
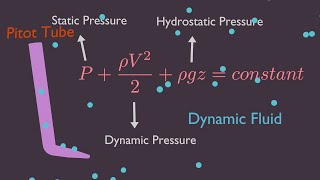
Correct! Dynamic pressure is associated with the kinetic energy of the fluid due to its motion. Remember the formula for dynamic pressure, it's given by: \( P_d = 0.5 \rho V^2 \).
What about stagnation pressure?
Great question! Stagnation pressure is the total pressure experienced by a fluid when it is brought to rest adiabatically. It combines both static and dynamic pressures, which we can write as: \( P_0 = P_s + P_d \).
So, remember, static pressure is when the fluid is stationary, dynamic pressure is due to motion, and stagnation pressure combines both.
Applications of Bernoulli’s Equation
Unlock Audio Lesson
Let's explore how Bernoulli's equation helps us in applications. Can anyone think of a common application of dynamic pressure?
Maybe in designing cars to reduce fuel consumption?
Absolutely! Car manufacturers use aerodynamic designs to minimize drag force, which is influenced by dynamic pressure. As part of this, what do you think happens to drag coefficients over time?
They’ve decreased significantly as car shapes have evolved, right?
Correct! The coefficient has decreased from 0.8 to 0.15. This means cars are more fuel-efficient because they experience less drag. Remember, understanding fluid mechanics allows engineers to optimize designs.
Energy Gradients in Fluid Flow
Unlock Audio Lesson
Now, let’s talk about energy gradient lines and hydraulic gradient lines in fluid mechanics. Why do you think these lines are important?
They probably help us visualize energy changes in fluid systems?
Exactly! The energy gradient line represents the total energy of the fluid, while the hydraulic gradient line considers only the static pressure and elevation heads. Can someone tell me what influences these lines?
Changes in fluid velocity and pressure, I suppose?
Yes! Any variation in energy levels affects how we draw these lines. Energy flows from high to low, guiding the flow direction and understanding energy losses.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The dynamic pressure is a key component of Bernoulli's equation that examines the energy associated with fluid flow. This section explores the definitions of static, dynamic, and stagnation pressures, and details their significance in real-world applications such as in pipe systems and automotive design.
Detailed
Dynamic Pressure
This section explores the intricate concepts of dynamic pressure in fluid mechanics, particularly as it relates to Bernoulli's equation. Dynamic pressure is one of the fundamental pressure types, along with static and stagnation pressures, that help us understand the energy distribution in flowing fluids. The significance of these pressures lies in their application across various engineering fields, including civil and mechanical engineering.
Key Points Covered:
- Definitions of Pressures: The section details the definitions of static, dynamic, and stagnation pressures, demonstrating how these measures contribute to an overall understanding of fluid behavior.
- Applications of Bernoulli’s Equation: Real-world scenarios, such as automotive design and fluid flow through pipes, illustrate the practical applications of these concepts. For example, the evolution of car designs to minimize drag force showcases how dynamic pressure can influence fuel efficiency.
- Kinetic Energy Correction Factors: It discusses the need for correction factors when considering non-uniform flow distributions, enhancing the practical application of Bernoulli’s equation.
- Energy and Hydraulic Gradient Lines: Understanding how these concepts relate to the flow of fluids in pipes and channels, helping engineers design more efficient systems.
- Flow Measurement Techniques: Methods such as using orifice meters and venturimeters guided by Bernoulli’s principles are explored for empirical analysis of fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Pressure Types
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fourth part, I will talk about how we can define the three different types of pressures; static, dynamic and stagnation pressures.
Detailed Explanation
In fluid mechanics, pressure is a crucial concept used to describe the forces acting on fluids in motion. There are three main types of pressure: static pressure, dynamic pressure, and stagnation pressure. Static pressure is the pressure exerted by a fluid at rest, and it is the pressure we feel when we dive underwater. Dynamic pressure depends on the fluid's velocity and can be calculated using the formula: Dynamic Pressure = (1/2) * ρ * V², where ρ is the fluid density and V is the fluid velocity. Stagnation pressure combines both static and dynamic pressure and measures the pressure when a fluid comes to a complete stop, like when air flows into a pitot tube on an aircraft. Understanding these different types of pressures helps engineers design better fluid systems.
Examples & Analogies
Think of a water faucet. When you open it, the water flows out with force (dynamic pressure). If you were to place your thumb partially over the opening, you would feel the water pushing against your thumb, which constitutes the static pressure. When you completely cover the opening, the water backs up until it stops flowing, creating stagnation pressure at that point where the water is momentarily at rest.
Bernoulli's Equation and Pressure Relationships
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, in terms of pressures, if you talk about, one is static pressure, that is the presses act on this fluid particles another is the dynamic pressure because of the velocity components.
Detailed Explanation
Bernoulli's equation presents a relationship between static pressure, dynamic pressure, and potential energy. It asserts that for an incompressible, non-viscous fluid flowing within a streamline, the total mechanical energy per unit volume remains constant. This means that the sum of the static pressure (the pressure in a resting fluid), dynamic pressure (due to the fluid's motion), and potential energy (due to height) is consistent along a streamline. For example, if a fluid speeds up, the dynamic pressure increases, and the static pressure decreases, demonstrating the conservation of energy within the fluid.
Examples & Analogies
Imagine a garden hose with water flowing through it. When you partially block the end of the hose with your finger, the water accelerates and shoots out more forcefully while the pressure at the hose's opening decreases. This illustrates how static pressure drops as the dynamic pressure from the fluid's speed increases, embodying Bernoulli's principle.
Applications of Dynamic Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So to measure the air speed in any modern aircraft, still also use the same concept of the measuring the pressures and as you measure the pressures at this stagnation point and you know the atmospheric pressures, then we can easily find out what could be the airspeed is coming.
Detailed Explanation
In aviation, dynamic pressure is critical for determining airspeed. Instruments like pitot tubes measure the stagnation pressure, which provides crucial information about the fluid dynamics around the aircraft. By comparing the stagnation pressure to the ambient (static) atmospheric pressure, pilots can determine the aircraft's current speed. This measurement is essential for safe flight operations and performance calculations.
Examples & Analogies
Think of how a car's speedometer works. Just as it measures how fast the car is moving by interpreting how much air pressure pushes against a small opening, a pilot’s pitot tube calculates the speed of the airplane by measuring the difference between static pressure and dynamic pressure. This difference helps pilots understand how fast they are flying through the air, ensuring a safe flight.
Understanding Stagnation Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if you look it that same concept what we are talking about. As I say that the sum of the static and dynamic pressure is called the stagnation pressure.
Detailed Explanation
Stagnation pressure is a fundamental concept in fluid mechanics, representing the maximum pressure experienced by a fluid when it is brought to a complete stop. It can be viewed as the sum of static pressure and dynamic pressure. When a fluid flows into a stagnation point, all its dynamic energy converts to pressure energy, thus giving rise to the stagnation pressure. It is vital for accurately assessing pressures in various fluid applications such as aerodynamics and hydraulic systems.
Examples & Analogies
Imagine a water slide. As you reach the bottom, the fast-moving water suddenly stops, creating a splash and a wave. The pressure you feel at this moment is similar to stagnation pressure—the energy of the water's motion has fully converted into pressure, compacting against you as you arrive at a stop.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dynamic Pressure: Represents the kinetic energy of flowing fluid.
-
Static Pressure: Exists in a static fluid, exerted uniformly in all directions.
-
Stagnation Pressure: The combined effect of static and dynamic pressure when fluid comes to a stop.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The use of pitot tubes in aircraft to measure airspeed based on dynamic pressure.
-
Automobile shapes designed to minimize aerodynamic drag, influencing fuel efficiency.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Dynamic flows mean kinetic shows, static rests while pressure goes!
📖 Fascinating Stories
-
Imagine a calm lake (static pressure) versus a rushing river (dynamic pressure). The lake holds its peace, while the river's energy flows freely, racing down to sea level (stagnation).
🧠 Other Memory Gems
-
SDS for remembering: S = Static, D = Dynamic, S = Stagnation!
🎯 Super Acronyms
PEF
- Pressure
- Energy
- Flow - connects all components of Bernoulli’s principles!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dynamic Pressure
Definition:
The pressure associated with the kinetic energy per unit volume of a fluid flow.
-
Term: Static Pressure
Definition:
The pressure exerted by a fluid at rest.
-
Term: Stagnation Pressure
Definition:
The total pressure of a fluid when it is brought to rest; the sum of static and dynamic pressures.
-
Term: Bernoulli's Equation
Definition:
An equation representing the conservation of energy in a flow of an incompressible fluid.
-
Term: Coefficient of Discharge
Definition:
The ratio of actual discharge to theoretical discharge in fluid flow devices.