Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stagnation Pressure
Unlock Audio Lesson
Today, we'll explore **stagnation pressure** and how it plays a crucial role in fluid mechanics. Can anyone tell me what components are involved in stagnation pressure?
Is it static and dynamic pressure?
Exactly right! Stagnation pressure is the sum of static pressure, which arises from the fluid's weight, and dynamic pressure, which is related to its velocity. Remember: **Pressure = Static + Dynamic**.
How do we measure stagnation pressure?
Great question! We typically use devices like **Pitot tubes** to measure stagnation pressure in fluid flows.
What's the significance of knowing this pressure?
Knowing stagnation pressure helps us compute flow velocity and understand energy losses in systems. A useful mnemonic to remember is **'Static + Dynamic = Stagnation.'**
Can we see how this is applied in real-world scenarios?
Absolutely! Let’s dive into real-world applications involving stagnation pressure next.
Understanding Energy Gradient and Hydraulic Gradient Lines
Unlock Audio Lesson
Now that we've discussed stagnation pressure, let’s talk about **energy gradient lines** and **hydraulic gradient lines**. Who can explain what these terms mean?
Are they related to energy levels in fluid flow?
Exactly! The energy gradient line represents the total energy head of the fluid, while the hydraulic gradient line measures pressure and elevation. The energy gradient includes **static pressure**, **dynamic pressure**, and **elevation energy.**
So, the hydraulic gradient line doesn’t consider velocity then?
Correct! The hydraulic gradient only considers static pressure and elevation. A good way to remember this is to associate 'Energy = Static + Dynamic + Elevation', while 'Hydraulic = Static + Elevation'.
When would we practically use these concepts?
In designs of pipes and channels, knowing how to plot these lines can help engineers predict flow behaviors and address energy losses effectively.
Can you give a quick summary for us?
Sure! To summarize, stagnation pressure is crucial for flow measurements, energy gradient lines include all energy components of fluid flow, while hydraulic gradient lines help in understanding pressure and elevation without velocity considerations.
Applications and Examples of Stagnation Pressure
Unlock Audio Lesson
Let’s relate stagnation pressure to practical devices. Why are **Pitot tubes** significant in fluid dynamics?
They measure flow velocity?
Correct! They help compute airspeed in aircraft. Can anyone explain how it does this?
By measuring stagnation pressure and comparing it with atmospheric pressure?
Exactly! With that comparison, we can derive the flow velocity using Bernoulli's principle.
What other applications exist beyond aircraft?
Great thought! They're also used in determining velocities in pipe flows and even in meteorology to gauge wind speeds.
So it connects to various fields!
Yes, indeed! Stagnation pressure is a versatile concept essential across multiple engineering domains.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Stagnation pressure is defined as the total pressure experienced by a fluid when brought to rest is an amalgamation of static and dynamic pressures. The significance of stagnation pressure is highlighted through examples such as pitot tubes used in measuring fluid velocities and applications of Bernoulli's equation in real-world scenarios.
Detailed
Detailed Summary of Stagnation Pressure
In the context of fluid mechanics, stagnation pressure refers to the pressure exerted by a fluid at a point where it is brought to a complete stop. This pressure can be mathematically represented as a sum of two components: static pressure and dynamic pressure. Static pressure exists due to the weight of the fluid, while dynamic pressure is related to the fluid's velocity.
The significance of stagnation pressure is underscored in applications such as Pitot tubes, which are essential in measuring flow velocities in various engineering scenarios, including aerodynamics and hydraulics. The relationship exhibited through the Bernoulli equation illustrates that energy conservation principles govern the behavior of fluids in motion. As fluid flows from higher energy states to lower energy states, analyzing stagnation pressure provides valuable insights into system efficiency and performance.
Additionally, understanding the differences between energy gradient lines and hydraulic gradient lines is critical. The energy gradient line encompasses all energy components including pressure, velocity, and elevation. In contrast, the hydraulic gradient line considers only pressure and elevation. This analysis is essential when designing systems and predicting fluid behavior in channels and pipelines.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Stagnation Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
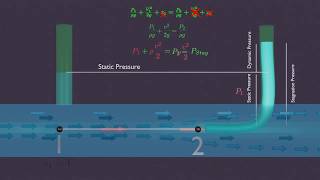
The sum of the static pressure and dynamic pressure is called the stagnation pressure. Whenever you have an object which is at stationary conditions, it is at rest conditions. At that point, the pressure will be because the velocity at that point of the fluid flow have to be zero. So we get is the stagnation pressure, we will have a two components: one is a static pressure component and another is dynamic pressure component.
Detailed Explanation
Stagnation pressure is a concept in fluid mechanics that helps us understand pressure within a moving fluid. When a fluid flows and comes to a complete stop, all the kinetic energy of the fluid is converted into pressure energy. The stagnation pressure can be understood as the total pressure at that point, which consists of two parts: the static pressure (the pressure exerted by the fluid at rest) and the dynamic pressure (the pressure due to fluid motion). At the point where the fluid is completely stopped, the dynamic pressure becomes zero, and thus the stagnation pressure is equal to the static pressure plus the kinetic energy per unit volume represented as pressure.
Examples & Analogies
Think about a garden hose. When you place your thumb over the end of the hose while water is flowing, the water can't escape immediately. At the point where your thumb blocks the flow, the water builds up and you feel a strong pressure. This pressure is similar to stagnation pressure: the dynamic pressure of the moving water converts to static pressure as it comes to a stop.
Measurement with Pitot Tubes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
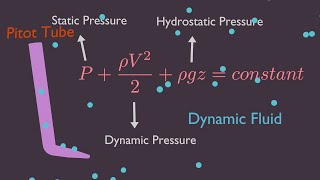
Using a pitot tube, which can insert and have a sharp point to rise the fluid inside the tube, that is what measures both the components, the dynamic pressure as well as the static pressures.
Detailed Explanation
A pitot tube is an instrument used to measure the flow velocity of fluids. It measures the stagnation pressure by having a tube open to the flow. The fluid enters the tube and has a velocity of zero at the opening, which allows for the measurement of the maximum pressure exerted by the fluid. By comparing this stagnation pressure to a reference static pressure (obtained from another measurement point), one can determine the dynamic pressure and subsequently calculate the fluid velocity using Bernoulli's equation.
Examples & Analogies
Consider a car moving at high speed. To measure how fast it’s going, we can look at the air pressure hitting the front of the car (like the fluid in a pitot tube). If the car were to stop suddenly, all that air pressure would create a 'build-up,' similar to the water backing up when you put your thumb over the hose. By assessing this pressure difference, we determine the speed of the car just like we calculate fluid velocity using a pitot tube.
Applications in Aerodynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The same concept of the pitot tubes allows us to measure air speed in modern aircraft. As you measure the pressures at this stagnation point, you know the atmospheric pressures, and then we can easily find out what could be the airspeed.
Detailed Explanation
In aviation, pitot tubes are critical for measuring the speed of aircraft relative to the surrounding air. The tube measures the stagnation pressure of the airflow combined with atmospheric pressure, allowing pilots to receive accurate readings of airspeed essential for flight operations. This measurement is crucial for safe navigation and flight control, as it affects lift and drag forces on the aircraft.
Examples & Analogies
Imagine a pilot flying an airplane. Just like a speedometer in a car tells the driver how fast they are going, the pitot tube gives pilots real-time airspeed data based on changes in air pressure. If the pilot knows their speed relative to the air, they can adjust the altitude and flight path safely and efficiently.
Stagnation Streamline
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The flow streamline that extends from upstream to the stagnation point is called the stagnation streamline, which is just come and hit over the mouth of the pitot tube.
Detailed Explanation
The stagnation streamline represents the path that fluid particles travel as they flow toward the pitot tube. At the stagnation point, the fluid is brought to rest; this streamline is crucial in understanding how pressure and velocity changes occur in a flowing fluid system. It is the visual representation of how fluid slows down as it encounters an obstruction (such as a pitot tube) and is instrumental in analyzing fluid flow characteristics.
Examples & Analogies
Think of water flowing in a river that reaches a large rock in the center of the water flow. The water on the upstream side of the rock flows towards the rock until it hits it and momentarily slows down before flowing around it. The water's path to that rock is akin to the stagnation streamline towards a pitot tube, where the water is momentarily stopped to create pressure.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stagnation Pressure: The total fluid pressure when brought to rest; sum of static and dynamic pressures.
-
Static Pressure: Pressure due to the weight of the fluid at rest.
-
Dynamic Pressure: Pressure related to fluid velocity, vital for calculating flow speed.
-
Pitot Tube: Instrument used for measuring stagnation pressure and thus flow speed.
-
Energy Gradient Line: All energy components represented visually in fluid flow.
-
Hydraulic Gradient Line: Visual representation of pressure and elevation in fluid flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The use of Pitot tubes in aircraft to measure airspeed is a practical application of stagnation pressure.
-
In civil engineering, understanding the hydraulic gradient line helps in designing effective water supply systems.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Static is stress that holds you near, Dynamic's what moves, makes matters clear. Together they mix, in a pressure so dear, Stagnation holds fast, let’s give it a cheer!
📖 Fascinating Stories
-
Imagine a river flowing fast down a hill. When it meets a dam, it stops; that’s the stagnation point. The water pressure builds up from both stillness (static) and flow (dynamic) to create the highest pressure at the dam.
🧠 Other Memory Gems
-
Remember: 'STATIC + DYNAMIC = STAGNATION' for understanding the components of stagnation pressure.
🎯 Super Acronyms
For EGL and HGL, remember 'EGL = Energy Get Line' and 'HGL = Hydro Get Line'.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stagnation Pressure
Definition:
The total pressure a fluid exerts when brought to a complete stop, composed of static and dynamic pressure.
-
Term: Static Pressure
Definition:
The pressure exerted by a fluid due to its weight when not moving.
-
Term: Dynamic Pressure
Definition:
The pressure associated with the fluid's velocity, calculated as 1/2 * density * velocity^2.
-
Term: Pitot Tube
Definition:
A device used to measure fluid flow velocity based on stagnation pressure.
-
Term: Energy Gradient Line (EGL)
Definition:
A graphical representation of the total energy of fluid flow, including static, dynamic, and elevation components.
-
Term: Hydraulic Gradient Line (HGL)
Definition:
A graphical representation of the static pressure and elevation in fluid flow, excluding dynamic pressure.