Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Drag Force
Unlock Audio Lesson
Today, we will discuss drag force and its impact on fuel efficiency. Can anyone tell me what drag force is?
Is it the resistance a car faces when moving through air?
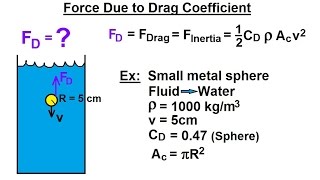
Exactly! The drag force depends on factors like the shape of the vehicle, the density of air, andVelocity. The formula is: $F_D = C_D \cdot \frac{1}{2} \cdot \rho \cdot V^2 \cdot A$. Remember this as the 'Drag Force Equation'!
What's the significance of the drag coefficient?
Good question! $C_D$ indicates how aerodynamic a vehicle is—lower values mean less resistance. Think of $C_D$ as the 'dragginess' rating of a vehicle.
How has the drag coefficient changed over time?
Historically, the drag coefficients improved from around 0.8 to as low as 0.15. That means car design has drastically changed for better aerodynamics!
Why does reduced drag lead to improved fuel efficiency?
Less drag means the engine does not have to work as hard to overcome air resistance, saving fuel. Let's keep this in mind as we explore more about fluid dynamics!
Practical Examples of Drag Force
Unlock Audio Lesson
Let's dive deeper into how drag force affects real vehicles. Can anyone think of an example of a fuel-efficient car?
Tesla cars are designed for aerodynamics!
Correct! Their sleek shapes minimize drag force. As the drag coefficient decreases, fuel consumption decreases. How much do you think it impacts fuel efficiency?
Maybe a lot? Like how much fuel would be saved over a distance?
Exactly! If a car of 6 liters needed only 1 liter over a set distance, that showcases the importance of design. Reducing $C_D$ dramatically improves efficiency.
What factors led to the reduction in drag coefficients?
Experiments on shapes, materials, and even computational fluid dynamics have played roles in evolving car designs. All aiming for that minimum drag coefficient of 0.15.
It's fascinating how engineering impacts everyday life!
Absolutely! This understanding benefits not just efficiency, but also sustainability. Great insights, everyone!
Applications of Bernoulli's Equation
Unlock Audio Lesson
Now, let's connect our understanding of drag force to Bernoulli's equation. Who remembers the equation?
Bernoulli's equation includes pressure energy, kinetic energy, and potential energy?
Exactly! It's essential in understanding how to minimize drag. By optimizing these energies in our designs, we can also reduce fuel consumption.
So it's all about balance and flow?
Absolutely! Think of it as harmonizing energy within a fluid system to create smoother flows. That reduces drag significantly.
What other systems use these principles?
From airplane wings to the design of pipelines, all applications utilize Bernoulli’s principles! Always connecting this back to minimizing resistance.
This is really connecting the dots between theory and practice!
Certainly! Understanding these principles helps engineers innovate as they face real-world challenges. Excellent job today!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on how advancements in car design have led to a dramatic reduction in drag coefficients, thus improving fuel efficiency. It highlights the historical context of drag force measurements and elaborates on practical examples and applications in fluid mechanics.
Detailed
Drag Force and Fuel Efficiency
The drag force experienced by a vehicle is a critical factor in fuel efficiency. Since the 1800s, the coefficient of drag (CD) for vehicles has significantly improved due to advancements in design, moving from approximately 0.8 to a theoretical minimum of about 0.15 by 2020. This improvement showcases how aerodynamic shapes have evolved to minimize drag, directly correlating to reduced fuel consumption. The equation for drag force is defined as:
$$ F_D = C_D \cdot \frac{1}{2} \cdot \rho \cdot V^2 \cdot A $$
Where:
- $F_D$ = Drag Force
- $C_D$ = Drag Coefficient
- $\rho$ = Density of air
- $V$ = Velocity of the vehicle
- $A$ = Projected area of the vehicle
Overall, understanding drag force is paramount in automotive engineering, as it informs the design processes that lead to more fuel-efficient vehicles. By minimizing drag, manufacturers can significantly enhance fuel efficiency, reducing both costs for consumers and environmental impact.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Drag Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As you know, people say as of now, we have very fuel-efficient cars. That means the mostly car we talk about the drag force. The more the drag force, then you have to have more fuel to be spent it, fuel to burn it. So the basic idea is to, because V stands for the design velocities, area is a projected area, which is more or less constant. So, rho is the density of air. Only the C can be changed.
Detailed Explanation
Drag force is a resistance force that acts opposite to the direction of motion of a vehicle. In the context of cars, a key factor is how much fuel is consumed, which is directly related to this drag force. The drag force depends on three main parameters: the vehicle's velocity (V), the shape and size of the vehicle (area), and the density of the air (rho). The drag coefficient (C) may be adjusted to optimize performance. Reducing drag can lead to more fuel-efficient vehicles by requiring less energy to maintain speed.
Examples & Analogies
Think of riding a bicycle. When you ride fast, especially against the wind, it feels harder to pedal—that's drag at work. If you were to change your body position to be more aerodynamic, similar to how modern cars are designed with sleek shapes, you could reduce that drag and ride more easily, needing less energy.
Evolution of Drag Coefficient
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The coefficient of drag, which earlier was close to 0.8, that means the force is equal to 0.8 times of rho V square into the area, has been reduced to 0.15, very close to theoretical value. This reduction is due to the change in the shape of the cars and the advancement in fluid mechanics.
Detailed Explanation
Over the last 120 years, automotive design has evolved significantly, leading to a decrease in the drag coefficient from about 0.8 to 0.15. This means that modern cars can move through the air more efficiently, requiring less fuel for the same amount of distance traveled. The reduction in the drag coefficient indicates that the designs have become more streamlined, allowing smoother airflow around the vehicle, which minimizes energy loss due to drag.
Examples & Analogies
Consider how airplanes and sports cars are shaped for speed—a long, smooth design helps them move quickly through the air. In contrast, a box-shaped vehicle creates more resistance and therefore needs more energy (or fuel) to maintain speed, much like trying to run while pushing a shopping cart versus running freely.
Impact on Fuel Efficiency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For example, if a car used to take 6 liters of fuel to travel a certain distance, it can now travel the same distance with just 1 liter due to the significant reduction in drag coefficient.
Detailed Explanation
This dramatic improvement in fuel efficiency illustrates the impact of reducing drag on overall vehicle performance. The relationship can be viewed mathematically, showing that lower drag means less fuel consumption for the same speed. Therefore, advancements in vehicle design directly contribute to significant savings in fuel costs over time.
Examples & Analogies
Imagine a car that previously needed six soda bottles of gasoline to reach a specific destination. Now, through better design, the same journey only requires one soda bottle. This represents both a financial savings for the driver and a reduction in environmental impact.
Contributions from Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The improvements in automotive design have resulted from extensive research and experimentation in fluid mechanics aimed at minimizing the drag coefficient to near its theoretical minimum.
Detailed Explanation
Fluid mechanics has played a crucial role in the automotive industry by helping engineers understand and quantify how air flows around vehicles. Through experiments and simulations, they can refine shapes and designs to ensure that vehicles encounter minimal resistance as they move. This study not only enhances performance but also addresses environmental concerns by lowering fuel consumption.
Examples & Analogies
Just like how scientists study nature to create efficient designs—like bird wings or fish bodies—automotive engineers use the same principles to create cars that glide smoothly through air, ensuring we can drive faster and burn less fuel.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Drag Force: The force opposing the motion of an object through fluid, impacting its fuel efficiency.
-
Drag Coefficient: A value indicating how aerodynamic a shape is, critical for vehicle fuel efficiency.
-
Bernoulli's Principle: Describes the relationship between pressure, velocity, and energy in fluid flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Modern electric cars like Tesla utilize streamlined designs to lower their drag coefficients, thus improving fuel efficiency.
-
Historical cars had drag coefficients close to 0.8, while aerodynamic advancements have brought this down to about 0.15 today.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
The drag force is strong but can be made light, with C_D low, efficiency shines bright.
📖 Fascinating Stories
-
Imagine a race car streamlined like an arrow. The smoother it is, the less gas it needs to flow faster. All about reducing drag!
🧠 Other Memory Gems
-
For drag force equations remember: 'Froggy Can Jump Very Amazingly' (F_C_D = V^2 * A).
🎯 Super Acronyms
DAME
- Drag
- Area
- Mass
- Efficiency — remember the factors influencing drag.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Drag Force
Definition:
The resistance experienced by an object when moving through a fluid, particularly air, which affects fuel efficiency.
-
Term: Drag Coefficient (C<sub>D</sub>)
Definition:
A dimensionless number indicating how aerodynamic an object is; lower values suggest better aerodynamic efficiency.
-
Term: Bernoulli's Equation
Definition:
A principle that describes the conservation of energy in flowing fluids, relating pressure, velocity, and elevation.