Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Hydraulic and Energy Gradient Lines in Open Channel Flow
Unlock Audio Lesson
In open channel flow, the hydraulic gradient line coincides with the free surface of the liquid. This occurs because there is no pressure head. Can anyone explain why the velocity head is important in understanding energy gradient lines?
The velocity head shows us the kinetic energy of the fluid above the free surface. It helps us calculate the total energy in the system.
Exactly! The energy gradient line includes the velocity head. Now, what happens to these lines when there are mechanical energy losses?
They slope downward in the direction of the flow because energy is lost due to friction.
Great! So, remember, the downward slope in these lines indicates energy losses, which impact system efficiency.
Comparison of Open Channel vs Pipe Flow
Unlock Audio Lesson
Let’s contrast open channel and pipe flow. In pipe flow, we often measure pressure using piezometers. What significance does this have?
It allows us to see how pressure varies within the pipe, especially how it relates to the hydraulic gradient.
Right! Gauge pressure plays a crucial role here. Can anyone tell me when it becomes zero?
At the pipe outlet when the flow exits into the atmosphere, it equates to atmospheric pressure.
Perfect! This clearly illustrates the fundamental concept regarding how pressure affects flow efficiency in our systems.
Mechanics of Pumps and Turbines
Unlock Audio Lesson
Now, let’s discuss mechanical energy devices like pumps and turbines. Who can explain the function of a pump in a hydraulic system?
A pump transfers mechanical energy to fluid by increasing its pressure.
And turbines do the opposite, extracting mechanical energy from the fluid and reducing pressure.
Exactly! Pumps enhance energy while turbines extract energy. What should we focus on when calculating their efficiency?
We should look at the mechanical power input and output ratios.
Very good! Keeping track of efficiencies helps us design more effective hydraulic systems.
Energy Losses and Efficiency in Systems
Unlock Audio Lesson
Let's dive deeper into energy losses. What are common causes of these losses in flow systems?
Friction, turbulence, and mechanical inefficiencies in pumps and pipes.
Exactly! These lead to a downward slope in our energy gradient lines. How can we express these losses?
We can express them through an efficiency equation, comparing input to output energy.
Well said! Efficiency is critical in understanding the performance of hydraulic systems. Every time you measure energy, think about where losses occur.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores the behavior of hydraulic and energy gradients in open channel and pipe flow systems, detailing how pressure differences affect flow efficiency. It highlights the significance of mechanical energy losses in maintaining system performance and the functioning of pumps and turbines as energy-enhancing and extracting components respectively.
Detailed
Efficiency of Systems
This section provides a comprehensive exploration of hydraulic systems, focusing on key factors that affect their efficiency.
Here are the main points:
- Hydraulic Gradient Lines: In open channel flow, the hydraulic gradient coincides with the free surface of the liquid as there's no pressure head; thus, it reflects the actual water surface level. In contrast, pipe flow utilizes pressure measurements, represented by hydraulic gradient lines, that connect to the piezometric levels of the fluid.
- Energy Gradient Lines: These lines incorporate the velocity head above the free surface, indicative of potential energy in the flow that can be converted to work by pumps or turbines. Understanding how hydraulic and energy gradients slope downstream due to mechanical losses addresses energy efficiency in these systems.
- Mechanical Energy Losses: Energy losses due to frictional effects lead to downward slopes in energy and hydraulic gradients, which indicates inefficiencies. The section clarifies that when gauge pressure is zero, it can signify conditions at the pipe outlet, equalizing to atmospheric pressure.
- Pumps and Turbines: Pumps are responsible for transferring mechanical energy to fluids, effectively raising pressure and energy within the system. Conversely, turbines extract energy from flowing fluids by dropping pressure, with efficiency being a crucial focus when calculating performance.
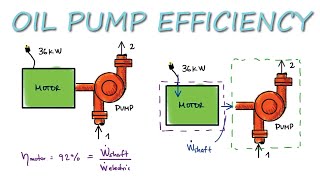
- Efficiency Calculations: The concept of efficiency checks the ratio of mechanical energy input to output. The section outlines basic calculations including the application of mass and energy conservation laws, which are essential for understanding variations in power and energy production in hydraulic systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Hydraulic and Energy Gradient Lines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Whenever a pipe exits, the pressure head becomes atmospheric pressure. The hydraulic gradient lines coincide with the pipe outlet where the pressure head becomes zero. In contrast, the energy gradient line includes the velocity head above the free surface and slopes downward in the direction of flow due to mechanical energy losses.
Detailed Explanation
In this chunk, we learn about the relationship between hydraulic gradient lines and energy gradient lines in fluid systems. When fluid exits a pipe, the pressure head reduces to atmospheric pressure, which means the hydraulic gradient line aligns with the outlet of the pipe. In open channel flow, there is no pressure head, and the hydraulic gradient coincides with the water's surface. The energy gradient line, however, accounts for losses in mechanical energy due to friction and other factors, resulting in a downward slope in the direction of the flow, indicating that energy is being lost along the flow path.
Examples & Analogies
Think about sliding down a hill on a smooth slide versus a rough slide. On the smooth slide, you can glide effortlessly, representing low energy loss. Conversely, if the slide were rough, you'd expend more energy overcoming friction to move down, akin to how the energy gradient line slopes downward due to energy loss in fluid systems.
Pressure Dynamics Relative to the Hydraulic Gradient Line
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When pressures in a flow section lie above the hydraulic gradient line, they are negative. This indicates that the section is under a lower pressure than the atmospheric pressure. Conversely, when pressures lie below the hydraulic gradient line, they are positive, indicating the section is under higher pressure than atmospheric pressure.
Detailed Explanation
This chunk explains the concept of pressure in relation to the hydraulic gradient line. If a fluid's pressure is above this line, it signifies a negative pressure situation, indicating the fluid is less than atmospheric pressure. Conversely, when the pressure is below the hydraulic gradient line, it is considered positive pressure. This understanding is crucial for solving fluid flow problems, as it helps identify whether there is sufficient pressure to maintain flow or if cavitation might occur.
Examples & Analogies
Imagine a balloon. When you squeeze it (like increasing pressure), you create a situation where the air inside is at a higher pressure compared to the surrounding atmosphere (positive pressure). If you poke a needle in it (like dropping pressure), the air rushes out rapidly (negative pressure scenario). Understanding how pressure works helps in designing systems that prevent balloon-like explosions or collapses.
Energy Manipulation in Pumps and Turbines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Pumps transfer mechanical energy to fluid by increasing pressure, whereas turbines extract energy from fluid by reducing pressure. The pump adds energy into the fluid system, while the turbine removes energy from it, essentially transforming mechanical energy into usable work.
Detailed Explanation
This chunk introduces the vital roles pumps and turbines play in fluid systems. Pumps increase the energy of the fluid by adding mechanical energy, which results in a rise in pressure. Conversely, turbines work in the opposite direction by extracting energy from the fluid and lowering its pressure. The distinction is crucial because it highlights how fluid systems can be designed for various applications, whether it’s generating power at hydroelectric plants or circulating water in irrigation systems.
Examples & Analogies
Consider a bicycle pump versus a bicycle pedal. When you push the pump, you’re forcing air into the tire, increasing its pressure—much like how a pump increases fluid pressure. On the other hand, when you're pedaling downhill, you're letting the energy of gravity do the work, akin to how a turbine extracts energy and reduces pressure.
Efficiency and Energy Losses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In every system, mechanical energy losses occur due to friction and heat. The efficiency of a system is defined as the ratio of useful output energy to input energy. This concept can be quantified for pumps and turbines, where each must maintain efficiency to ensure effective energy transfer from one form to another.
Detailed Explanation
This chunk addresses the concept of efficiency in systems dealing with fluid flow. It explains that due to various losses like friction, not all mechanical energy input translates to useful output. The efficiency can be expressed mathematically as the ratio of output energy over input energy. For hydraulic systems, keeping efficiency high is paramount, especially in applications like turbines, where maximum energy extraction is crucial to performance.
Examples & Analogies
Think of a car driving uphill. If it burns a lot of fuel just to overcome resistance (friction and air drag), it’s not using energy efficiently. However, a well-designed car with better aerodynamics and lighter materials will use less fuel to achieve the same task, much like an efficient turbine that maximizes energy extraction for minimal loss.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic Gradient Line: Coincides with free surface in open channel flow.
-
Energy Gradient Line: Includes kinetic energy in calculations.
-
Mechanical Energy Loss: Key factor influencing system efficiency.
-
Pump Efficiency: Ratio of output energy to input energy.
-
Turbine Efficiency: A measure of power extracted from fluid.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In an open channel, the hydraulic gradient coincides with the free surface, while in pipes, piezometers measure hydraulic gradient.
-
Mechanical energy loss can be quantified and directly affects the energy gradient, resulting in inefficiency during flow.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Water flows downhill, with pressure lost; In pipes and channels, we measure the cost.
📖 Fascinating Stories
-
Imagine a water park slide where the water flows smoothly down, but when it hits a rough patch, it slows down. This mimics how hydraulic systems lose energy through friction.
🧠 Other Memory Gems
-
Pumps Put Pressure, Turbines Take it Down - remember PPTD to recall their functions.
🎯 Super Acronyms
H.E.M.T - Hydraulic Gradient, Energy Gradient, Mechanical Losses, Turbines.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Gradient Line
Definition:
A line representing the total potential energy of the fluid, including kinetic energy in open channels.
-
Term: Energy Gradient Line
Definition:
A line that incorporates the velocity head above the free surface, indicating total energy including kinetic energy.
-
Term: Pressure Head
Definition:
The height of a fluid column that can be supported by the fluid's pressure.
-
Term: Mechanical Energy Loss
Definition:
The energy lost due to friction and turbulence, which affects the efficiency of hydraulic systems.
-
Term: Pump Efficiency
Definition:
The ratio of mechanical power output of a pump to the mechanical power input.
-
Term: Turbine Efficiency
Definition:
The ratio of mechanical power output of a turbine to the mechanical power input.