Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Hydraulic and Energy Gradient Lines
Unlock Audio Lesson
Let's begin by discussing the hydraulic and energy gradient lines. Can anyone tell me what they represent in an open channel flow?
The hydraulic gradient line matches the free surface, right? Because there's no pressure head.
Exactly! The hydraulic gradient line aligns with the free surface. Now, what about the energy gradient line?
It includes the velocity head above the free surface, showing total energy.
Great! You can remember that with the acronym HEV: Hydraulic Energy Velocity. The hydraulic line is flat, while the energy line includes kinetic energy as well. How do these lines behave in pipes?
In pipes, we use piezometers to measure pressure, and the energy line will slope down due to energy losses.
Well done! Energy losses due to friction cause the energy gradient line to slope downward. Remember, these principles are fundamental to designing effective hydraulic systems.
Pressure Dynamics in Flow Systems
Unlock Audio Lesson
Now let’s explore how pressure changes as flow exits pipes. Can anyone explain what happens at the pipe outlet?
At the exit, the pressure head drops to atmospheric pressure.
Correct! When this occurs, what can you tell me about the relationship between the hydraulic gradient line and the pipe outlet?
The hydraulic gradient line coincides with the pipe outlet because the pressure is atmospheric.
Exactly! And as fluid flows through the system, friction leads to mechanical energy losses. This concept reinforces why understanding these gradients is critical for engineers.
Does the gauge pressure affect how we interpret these lines?
Yes, great question! A gauge pressure above the hydraulic gradient line means negative pressure, while below indicates positive values. Remember this relationship as you analyze fluid systems.
Energy Extraction by Pumps and Turbines
Unlock Audio Lesson
Moving on, let’s discuss pumps and turbines. Can anyone share the difference in how they operate?
Pumps transfer mechanical energy to the fluid by raising its pressure.
Correct! And what about turbines?
Turbines extract mechanical energy from the fluid, which causes a drop in pressure.
Exactly! So we can see how energy is transferred and transformed in these systems. To help remember, think of the mnemonic P.E.T.: Pump Elevates, Turbine Extracts.
That’s an easy way to remember it!
Great! Understanding this will help you in applications like hydropower where the interaction between pumps and turbines is crucial.
Bernoulli's Equation Application
Unlock Audio Lesson
Lastly, let’s apply Bernoulli's equation in a practical example. Can anyone lay out the key terms in Bernoulli's principle?
It includes static pressure, dynamic pressure, and hydrostatic pressure.
Spot on! Now, how can you use this equation to evaluate energy differences in a system?
We can set up the equation for two points in the flow and analyze the pressure changes and energy conversion.
Exactly! Remember the acronym SP-DP-HP: Static Pressure, Dynamic Pressure, Hydrostatic Pressure. Using Bernoulli's equation helps identify how energy is conserved in systems.
This will help solve real-world engineering problems!
Absolutely. Apply these principles to calculate efficiencies and enhance the design of fluid systems effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on how turbines convert mechanical energy from fluids into usable energy. It explains key concepts such as hydraulic gradient lines, energy gradient lines, pressure differences in open channel flows and pipes, and the functioning of pumps and turbines in energy transfer, highlighting the mechanical energy losses due to friction.
Detailed
Energy Extraction by Turbines
In fluid mechanics, the application of energy principles is crucial to understanding how turbines extract energy from moving fluids. This section emphasizes the following key elements:
- Hydraulic and Energy Gradient Lines: In open channel flows, the hydraulic gradient line aligns with the liquid's free surface since there’s no pressure head, while the energy gradient line accounts for the velocity head above this surface. In contrast, pipes utilize devices such as piezometers for measuring pressures, demonstrating pressure changes along with flow.
- Defining Flow Mechanics: When fluids exit pipes to the atmosphere, pressure heads drop to atmospheric levels, indicating that hydraulic gradients coincide with outlet levels. As fluid moves, energy losses occur due to friction, showing a downward slope in both hydraulic and energy gradient lines. The relationship between gauge pressure and these lines forms the foundation for analyzing flow dynamics.
- Mechanics of Pumps and Turbines: Pumps increase the mechanical energy of fluids by raising pressures, while turbines remove or lower this pressure in energy extraction processes vital for hydropower applications. The section reinforces that pressure itself is not energy but rather a measure of potential energy per unit volume.
- Bernoulli's Principle Application: Exploring scenarios using Bernoulli's equation, students learn how to evaluate energy differences between flow sections. It shows the importance of efficiency, as real systems cannot convert total mechanical energy; losses in the form of heat and sound need consideration. Key concepts introduced include efficiency ratios for pumps and turbines, emphasizing their operational effectiveness.
Conclusively, this section integrates basic principles of hydraulics and energy transfer, establishing a comprehensive framework for understanding how turbines effectively harness energy from fluid flows.
Youtube Videos
![Power and Energy: Example 1: Part 1 [Fluid Mechanics #32]](https://img.youtube.com/vi/6PM15ec7oMs/mqdefault.jpg)
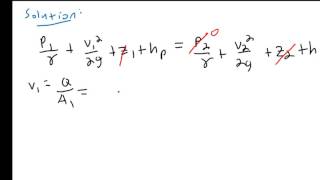
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Pressure Changes in Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now very basic things we should understand it, whenever a pipe exit, that means flow is going out. The pressure head becomes atmospheric pressure, no doubt about that. And that is the reason, the hydraulic gradient lines coincidence with the pipe outlet. So, when the pressure head becomes zero, that is what we said it, in case of open channel flow, when there is no pressure, is pressure is atmospheric pressure, that the surface becomes hydraulic gradient line.
Detailed Explanation
When water flows out of a pipe, the pressure inside the pipe drops to atmospheric pressure at the outlet. This condition causes the hydraulic gradient line, which represents how the pressure in the fluid changes with height, to align with the outlet of the pipe; because at this point, the pressure is no longer providing any head to push the fluid upwards. This understanding is crucial when analyzing fluid systems, especially when comparing open channel flows where pressure is not involved.
Examples & Analogies
Think about a water fountain: as the water exits the fountain and goes into the air, it no longer has the pressure from being contained in pipes; instead, it relies purely on the gravitational pull to fall back down. Similarly, once the water exits the pipe, it’s like the fountain, where it transitions from a pressurized system to an unpressurized one.
Energy Gradients and Losses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mechanical energy losses due to the frictional effects, which is converting from thermal energy, the causes the energy gradient line, hydraulic gradient line, to a slope downwards in the directions of the flow, that is what I try to explaining to you. There will be energy losses whenever you have the flow systems.
Detailed Explanation
As fluid flows through pipes, it encounters resistance from the pipe walls (friction). This resistance causes energy losses, meaning that not all the energy input into the system can be converted to kinetic or potential energy of the flowing fluid. In a graphical representation, both the energy gradient line and the hydraulic gradient line slope downwards, indicating that energy is being lost along the flow path, predominantly due to friction.
Examples & Analogies
Imagine sliding down a slide at a playground. If the slide is smooth, you go down quickly, but if it is rough, you slow down because of friction. Just like that, fluids lose energy traveling through pipes, particularly when the pipes are rough or damaged, causing them to lose speed and pressure.
Turbine Functionality and Energy Extraction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As you know it, the pump is transfer from mechanical energy to fluid by rising pressures. So, fluid gains the energy because of the pumping systems by rising its pressures, that is the. Similar way, the turbine does opposite things, that it takes out or extract the mechanical energy from the fluid by dropping it pressure.
Detailed Explanation
Pumps increase the energy of a fluid by acting on it with mechanical energy to raise its pressure and move it along a system. In contrast, turbines extract energy from a moving fluid, causing a drop in pressure as the fluid does work (like rotating the turbine blades). Understanding this relationship is crucial in energy management systems, especially in hydroelectric power generation.
Examples & Analogies
Consider a water wheel at a mill: when moving water hits the blades of the wheel, it turns the wheel, converting the fluid's energy into mechanical work (like grinding grain). Here, the turbine is extracting energy from the water flow, demonstrating how turbines can generate power from moving water.
Calculating Ideal Energy and Power
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This mechanical energy what we get it and if I multiply with a mass rate, I will get the work done part, okay. How much of work done we are getting it or how much power we are getting it, maximum ideal power generated by turbines will be m dash and the energy part.
Detailed Explanation
The concept of power in fluid dynamics can be understood through the product of energy and mass flow rate. When we talk about turbines, the power they can generate theoretically can be calculated by multiplying the mass flow rate of the fluid by the energy extracted per unit mass (often related to the drop in height or pressure). This helps engineers design systems that maximize the efficiency and output of turbines.
Examples & Analogies
Imagine a hydroelectric dam. Water from the reservoir has potential energy, which converts to kinetic energy as it flows down to the turbine. The more water that flows per second (mass rate), the more energy (and therefore power) can be produced, similar to how a bigger river can generate more electricity than a small stream.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic Gradient Line: The line representing hydraulic head in a fluid system that indicates pressure potential.
-
Energy Gradient Line: Demonstrates the total energy of fluid flow, incorporating both velocity and elevation aspects.
-
Mechanical Energy Losses: Reduce the efficiency of fluid systems due to irreversible energy transfers.
-
Turbine Efficiency: Measures how effectively a turbine converts fluid energy into mechanical energy.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a hydroelectric dam, water flows through a turbine, where it transforms kinetic energy into rotational energy, illustrating energy extraction principles.
-
The use of piezometers in pipe systems allows engineers to measure hydraulic heads, which assist in understanding pressure dynamics.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the channel flow so bright, hydraulic lines take flight; energy above the surface is a beautiful sight.
📖 Fascinating Stories
-
Once upon a time, in a fluid world, a water turbine danced, extracting energy from flowing streams, transforming potential into useful power, guided by the laws of nature.
🧠 Other Memory Gems
-
Remember SP-DP-HP for Bernoulli: Static Pressure, Dynamic Pressure, Hydrostatic Pressure.
🎯 Super Acronyms
HEV
- Hydraulic Energy Velocity to recall the relationship of hydraulic and energy lines.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Gradient Line
Definition:
The line representing the hydraulic head in a fluid system, coinciding with the free surface in open channel flow.
-
Term: Energy Gradient Line
Definition:
A line that represents the total energy of the flow, including kinetic and potential energies.
-
Term: Mechanical Energy Losses
Definition:
Losses in energy due to friction and turbulence in fluid systems.
-
Term: Bernoulli's Equation
Definition:
An equation that describes the conservation of energy in fluid flow, relating pressure, velocity, and height in a streamline.
-
Term: Turbine Efficiency
Definition:
The ratio of the mechanical power output of a turbine to the mechanical power input, indicating its operational effectiveness.