Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Hydraulic and Energy Gradient Lines
Unlock Audio Lesson
Let's start with the hydraulic gradient line. In open channel flow, this line coincides with the free surface of the liquid. Can anyone tell me why this is?
Because there's no pressure head in open channels?
Exactly! And now, how do we define the energy gradient line in such systems?
Is it the total energy head, including velocity head above the surface?
Correct! So, in an open channel flow, the energy gradient line is the hydraulic gradient line plus the velocity head, right? Remember this as we study more advanced concepts.
What happens in pipe flow then?
In pipe flow, we can measure pressure heads with instruments like piezometers and calculate energy gradient lines using a pitot tube. Let’s summarize: hydraulic gradient lines in channels align with the liquid's free surface, while energy gradient lines take velocity into account.
Pumps and Turbines
Unlock Audio Lesson
Next, let’s discuss pumps and turbines. A pump increases fluid pressure by transferring mechanical energy to it. Can anyone explain what a turbine does?
A turbine extracts mechanical energy from the fluid!
Great! So pumps raise energy, while turbines lower it. Remember the acronym PET: Pump Energy Transfer, and Turbine Energy Extraction. Can you think of where you see this in real life?
Hydropower plants use turbines to generate electricity!
Exactly! The energy exchange between pumps and turbines is crucial in engineering. Both systems reflect how energy losses can occur due to friction and other factors.
Bernoulli's Equation and Mass Conservation
Unlock Audio Lesson
Now, let's bridge these concepts with Bernoulli's equation. It relates pressure, velocity, and elevation in fluid flow. How does Bernoulli's principle connect to mass conservation?
I think it shows that as velocity increases, pressure decreases, right?
Exactly! This relationship helps us apply the principle of mass conservation effectively. What do we maintain as flow characteristics during Bernoulli's applications?
Incompressible, steady, and frictionless flow conditions?
Spot on! These assumptions help simplify our calculations. Remember, flow continuity is crucial when addressing flow problems through devices like venturi tubes.
Pressure Head and Energy Changes
Unlock Audio Lesson
Let’s talk about pressure heads now. How do the positions of pressure heads relate to the hydraulic gradient line?
If the pressure in a section lies above the hydraulic gradient line, it's negative?
Yes! While below this line means positive pressure. This is critical for solving flow problems. Reflect on this as we calculate pressure changes!
Can this be related to energy losses in the system?
Absolutely! Energy losses due to friction lead to differences in pressure at flow spots. Reserve this understanding for your calculations.
Practical Applications
Unlock Audio Lesson
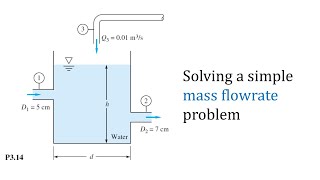
Finally, let’s explore practical applications of mass conservation! How can we calculate mass flow in real systems?
By applying the mass conservation equations alongside Bernoulli's equation?
Exactly! Think of real contexts where venturi tubes are utilized to measure flow rates based on pressure changes. How does this connect to efficiency?
Efficiency calculations might account for losses that impact our theoretical values.
Right! Calculate efficiency by comparing actual outputs to theoretical. Always keep a critical eye on how pressure and energy interplay in both pumps and turbines.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the principles of mass conservation in fluid dynamics. It explains how hydraulic and energy gradient lines behave in open channel flow and pipes, detailing the role of pressure heads, the concepts of pumps and turbines, and the significance of Bernoulli’s equation in analyzing fluid systems.
Detailed
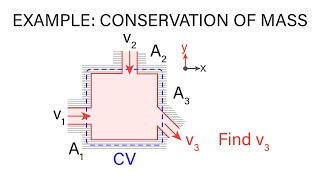
Mass Conservation
The principle of mass conservation is fundamental in fluid dynamics, asserting that mass cannot be created or destroyed in a closed system. This section primarily focuses on the behavior of hydraulic and energy gradient lines in open channel flows and pipelines. In open channel flow, the hydraulic gradient line aligns with the free surface of the liquid, as there is no pressure head. The energy gradient line includes the velocity head above the free surface, with mechanical energy losses causing a downward slope in both hydraulic and energy gradients.
The significance of this section lies in its connection with real-world applications such as pumps and turbines, where mechanical energy is converted into fluid energy. The section explains that pressure itself is a form of potential energy per unit volume, leading to variations in pressure at different points of flow.
Key to this discussion is Bernoulli’s equation, relating pressure, velocity, and elevation heads, and facilitating the analysis of fluid systems through mass conservation laws. The application of these concepts to various examples illustrates their practical relevance in engineering, specifically concerning flow measurement devices like venturi tubes and efficiency calculations of pumps and turbines.
Youtube Videos
![Conservation of mass (a.k.a., continuity) [Fluid Mechanics #2]](https://img.youtube.com/vi/PFgiW7P6omE/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Open Channel Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And okay, we are not discussing about open channel flow heads, but in case of open channel flow, the hydraulic gradient lines coincides with the free surface of the liquid okay. Because there is no pressure head. So, whatever the water surface free surface, that what will be hydraulic gradient line and the energy gradient lines will have a included the velocity head above the free surface.
Detailed Explanation
In open channel flow, the hydraulic gradient line aligns with the free surface of the liquid. This is because, unlike in closed systems, there is no pressure head acting in open channels. The hydraulic gradient hinges on the water's free surface, indicating how energy flows through this system. The energy gradient line, on the other hand, not only includes the hydraulic gradient but also adds the velocity head, which contributes to total energy measured in the system.
Examples & Analogies
Imagine a river where the water naturally flows and the surface of the water is what you can see. The very top of the water represents the hydraulic gradient line since there’s no enclosed pressure pushing the water down like you would find in pipes. The energy gradient might be likened to a surfer riding a wave, who has not just the height of the wave (hydraulic gradient) but also the speed with which they are moving down the wave (velocity head).
Hydraulic Gradient in Pipes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But in case of the pipes, we can have a piezometer to measure it, what could be the hydraulic gradient lines.
Detailed Explanation
In pipe systems, we utilize tools like piezometers to directly measure the hydraulic gradient. A piezometer is a device that gauges fluid pressure. When fluid flows through a pipe, knowing the pressure at various points allows us to determine how the hydraulic gradient changes. This is essential for understanding the flow dynamics and energy losses within the pipe system.
Examples & Analogies
Think of measuring water levels in different buckets lined up in a row—in this scenario, the piezometer acts as your measuring stick. Just like you can see how high the water level is in each bucket (reflecting the pressure at those points), the piezometer helps us visually track how the hydraulic gradient varies within the pipe system.
Pressure Changes in Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mechanical energy losses due to the frictional effects cause the energy gradient line, hydraulic gradient line, to slope downwards in the direction of the flow.
Detailed Explanation
As fluid flows through pipes, mechanical energy is lost mainly due to friction. This loss results in a downward slope of both the energy gradient line and the hydraulic gradient line. Essentially, as fluid progresses through the system, it loses energy, which is reflected in these gradients declining as they are measured downstream.
Examples & Analogies
Consider sliding down a waterslide; initially, you have high energy at the top, but as you slide down, friction with the slide reduces your speed and energy. Similarly, water flowing through pipes begins with a certain energy level, but friction reduces that energy as the water moves downstream.
Gauge Pressure Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The gauge pressure of the fluid is zero at the locations when the hydraulic gradient line intersects the fluids. Pressure in a flow section that lies above the hydraulic gradient line is negative and pressure in a section that lies below the hydraulic gradient line will be the positive value.
Detailed Explanation
Gauge pressure represents the pressure of fluid in relation to atmospheric pressure. When the hydraulic gradient intersects with the fluid, that point is considered to have zero gauge pressure. If the pressure in a flow section is above this line, it is regarded as negative as it falls below atmospheric pressure. Likewise, any pressure below the line is a positive value signifying a higher pressure than that intersection point.
Examples & Analogies
Imagine a balloon floating at a certain height; at that height, the pressure inside is equivalent to the surrounding atmosphere. If you push the balloon down into water, its pressure would increase—this is like being below the hydraulic gradient line (positive pressure). However, if you consider it at the surface of a lake, and the balloon is squeezing lightly, that may feel like it's experiencing a 'negative pressure' relative to the water above it.
Pump and Turbine Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As you know it, the pump transfers mechanical energy to fluid by rising pressures. Similar way, the turbine does the opposite things, that it takes out or extract the mechanical energy from the fluid by dropping its pressure.
Detailed Explanation
Pumps and turbines are integral components in fluid systems. Pumps increase the mechanical energy of a fluid, effectively raising its pressure. Conversely, turbines extract this mechanical energy from the fluid, which results in a drop in pressure. In practical applications, you’ll often see pumps in water supply systems, while turbines are common in hydroelectric power generation.
Examples & Analogies
Think of a small bicycle pump—when you pump air, you’re forcing it into the tire, increasing the tire's pressure (as in a pump). Conversely, consider a spinning water wheel in a river; as the water moves over it, the wheel spins and generates energy but also causes the water’s pressure behind it to drop, mimicking the action of a turbine.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic Gradient: Aligns with the free surface in open channels, showing potential energy.
-
Energy Gradient: Integrates kinetic and potential energy into one line.
-
Bernoulli's Principle: Relates fluid speed and pressure in flowing fluids.
-
Pumps: Devices that transfer energy to fluids, increasing pressure.
-
Turbines: Devices that convert energy from fluids into useful work.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of how a pump converts mechanical energy from a motor into hydraulic energy in water.
-
Illustration of a venturi meter demonstrating how flow rate can be calculated using pressure differences.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a flow, the gradient shows, where pressure from high to low flows.
📖 Fascinating Stories
-
Imagine a pump as a strong friend lifting a bucket of water, making it rise, while a turbine is like a swing that slows as you slide down.
🎯 Super Acronyms
Use the acronym HPET
- Hydraulic Gradient
- Pressure
- Energy Transformation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Gradient Line
Definition:
The line representing the potential energy head in a fluid, coinciding with the free surface in open channels.
-
Term: Energy Gradient Line
Definition:
The line representing total mechanical energy, including kinetic and pressure energy in fluid flows.
-
Term: Bernoulli's Equation
Definition:
A principle that expresses the conservation of energy in fluid dynamics, relating pressure, velocity, and height.
-
Term: Pump
Definition:
A device that increases the pressure of a fluid by adding energy to it.
-
Term: Turbine
Definition:
A device that extracts energy from fluid flow, reducing its pressure.
-
Term: Pressure Head
Definition:
The height of a fluid column that expresses its pressure energy relative to a specific reference point.