Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Hydraulic and Energy Gradient Lines
Unlock Audio Lesson
Today, we're diving into gradient lines in fluid mechanics, specifically the hydraulic and energy gradient lines. Who can tell me what a hydraulic gradient line represents?
Isn't it related to the pressure of the fluid?
Great observation! It represents the pressure head of the fluid. In open channel flow, it coincides with the free surface of the liquid. Can anyone explain what the energy gradient line includes?
It includes the velocity head as well, right?
Exactly! So the energy gradient line is always located higher than the hydraulic gradient line because it accounts for kinetic energy. Remember, 'Higher energy, greater velocity' to help you recall this. Let's move on to how these lines behave within pipes.
Do we measure these lines differently in pipes compared to open channels?
Yes! In pipes, we use piezometers and pitot tubes for measurements. Always remember: 'Piezometers for pressure, Pitot for velocity'. Let’s summarize: the hydraulic gradient shows pressure while the energy gradient accounts for both pressure and kinetic energy.
Mechanical Energy in Pumps and Turbines
Unlock Audio Lesson
Next, let’s explore pumps and turbines. Who can tell me what a pump does?
A pump moves fluid and increases its pressure!
Exactly! It transfers mechanical energy to fluid energy. And what about turbines?
Turbines extract energy from the fluid, right?
Correct! Turbines decrease fluid pressure by extracting mechanical energy. Remember this: 'Pumps go up, turbines let down' to keep it clear. Now, why is pressure so important in this context?
Because pressure represents potential energy?
Exactly! It’s potential energy per unit volume. Now think about how this relates to Bernoulli's principle and energy transformations. Let's summarize the roles — pumps add energy, turbines extract it.
Efficiency in Mechanical Systems
Unlock Audio Lesson
Now, let’s talk about efficiency in pumps and turbines. What does efficiency mean in our context?
It’s the ratio of useful output energy to input energy, right?
Exactly! So, if a pump's efficiency is 100%, it means all input energy is converted to output energy. Can someone explain why pumps and turbines never achieve 100% efficiency?
Because of energy losses, like heat or sound?
Exactly! Energy conversion isn't perfect, and that's where understanding these efficiency losses is crucial. Use this phrase: 'Efficiency reflects reality.' So, calculating efficiency helps us optimize systems and reduce wasted energy!
Application of Bernoulli's Equation
Unlock Audio Lesson
Finally, let’s see how we apply Bernoulli’s equation. Can anyone tell me its significance?
It shows the relationship between pressure, velocity, and height in fluid flow.
Correct! It helps us understand how energy is conserved in flowing fluids. Who can summarize what we’ve learned about energy losses in a pipeline?
Energy can be lost due to friction, converting mechanical energy into heat.
Exactly! The energy gradient line slope downwards in the direction of flow due to these losses. Always remember to consider energy losses when solving problems with Bernoulli’s equation. Let’s wrap up — understanding the integrity of energy is vital in fluid mechanics!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Mechanical energy is crucial in fluid systems and is characterized by the hydraulic and energy gradient lines. The section highlights how pumps increase fluid pressure and energy, while turbines extract energy from the fluid, along with the concept of efficiency in these systems and how losses affect overall performance.
Detailed
Mechanical Energy and Efficiency
This section explores the concepts of mechanical energy and efficiency in fluid mechanics, focusing primarily on the behavior of fluids in pipes and open channels. The hydraulic gradient line corresponds to the free surface of a liquid in open channel flow, while the energy gradient line factors in the velocity head above this free surface. In pipe flow, measurements can be taken using piezometers and pitot tubes to quantify these gradients.
A significant idea presented is that when fluid exits a pipe, the pressure head equates to atmospheric pressure, and the hydraulic gradient line aligns with the pipe outlet. Mechanical energy loss due to friction converts thermal energy into a downward slope of both energy and hydraulic gradient lines along the direction of fluid flow.
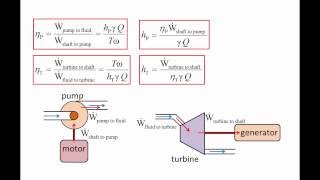
The discussion progresses to mechanical systems such as pumps and turbines. Pumps convert mechanical energy to fluid energy by increasing pressure; turbines do the reverse by extracting mechanical energy from the fluid. Pressure itself is identified as potential energy per unit volume, essential for understanding fluid dynamics. Bernoulli's equations illustrate the energy transformations between different states in a flowing fluid.
Lastly, the section addresses energy losses that prevent total energy conversion and introduces the concept of efficiency, defined by the ratio of output energy to input energy. Turbine and pump efficiencies are calculated similarly to understand the overall performance of a mechanical system.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Hydraulic Gradient and Energy Gradient Lines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In case of open channel flow, the hydraulic gradient lines coincide with the free surface of the liquid. Because there is no pressure head, the water's free surface represents the hydraulic gradient line. The energy gradient line includes the velocity head above the free surface.
Detailed Explanation
In an open channel flow, where water flows in a channel without confinement, the hydraulic gradient line is simply the same as the surface of the water. This relationship occurs because the pressure exerted by the water is equal to atmospheric pressure at the surface, meaning there is no additional pressure head at the surface itself. Thus, the hydraulic gradient line aligns with the water surface. Furthermore, the energy gradient line, which represents the total mechanical energy of the fluid, also accounts for the velocity of the flowing water. It is positioned above the hydraulic gradient line by an amount that reflects the velocity head, which is a measure of the kinetic energy of the water at that point.
Examples & Analogies
You can think of it as a slide in a playground: the height of the slide represents the hydraulic gradient, and if you were to slide down quickly, the speed you're going adds to how inclined the slide feels—similar to how the energy gradient includes both the height and the speed of the flow.
Pressure Heads in Pipe Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Typically, when flow exits a pipe into the atmosphere, the pressure head becomes atmospheric pressure. This is why the hydraulic gradient line coincides with the pipe outlet.
Detailed Explanation
In pipe systems, when water flows out of the pipe into the atmosphere, the pressure at the outlet drops to atmospheric pressure. This phenomenon causes the hydraulic gradient, which indicates the energy loss due to friction in the pipe, to line up with the level of the outlet of the pipe itself. Understanding this principle helps engineers calculate the energy dynamics and potential losses in water distribution systems.
Examples & Analogies
Imagine opening a soda can. As the pressure inside the can equalizes with the outside atmospheric pressure when opened, the soda starts flowing out smoothly, similar to how water exits a pipe and why measuring points are crucial for understanding how liquid flows.
Mechanical Energy Losses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mechanical energy losses due to friction convert mechanical energy into thermal energy, causing the energy and hydraulic gradient lines to slope downwards in the flow direction.
Detailed Explanation
As fluid flows through pipes or channels, friction with the walls leads to energy loss, transforming some of the mechanical energy (used to move the water) into thermal energy (which manifests as heat). This loss results in a downward slope of both the hydraulic and energy gradient lines in the direction of flow; essentially, the energy available for doing useful work reduces as water flows further from its source.
Examples & Analogies
Think of biking uphill (gaining energy) and then coasting downhill (losing energy due to friction and air resistance). The further you go downhill, the slower you become, just like how water loses energy as it moves through a pipe.
Efficiency of Mechanical Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Efficiency in mechanical systems like pumps and turbines is defined as the ratio of output mechanical energy to input mechanical energy.
Detailed Explanation
Efficiency is a critical concept in mechanical systems, quantifying how effectively energy is converted from one form to another. For example, in a pump, energy from an electric motor is transformed into mechanical energy to increase the pressure of the fluid. The effective use of this energy is measured in terms of efficiency, typically expressed as a percentage. High efficiency means minimal energy loss, whereas low efficiency indicates significant energy losses, often due to friction, heat, or other factors.
Examples & Analogies
Consider a light bulb: if it converts 80% of electrical energy into light and 20% into heat, its efficiency is 80%. Similarly, a highly efficient pump will ensure most of the input energy is used for moving water rather than wasted as heat or sound.
Power Generated by Turbines and Pumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mechanical energy converted to fluid through pumps and extracted from fluids through turbines ties back to the efficiency of these systems.
Detailed Explanation
Pumps and turbines function in opposite manners within a fluid system. A pump increases the mechanical energy of the fluid by raising its pressure, effectively allowing stored energy to do work. Conversely, when a fluid passes through a turbine, its mechanical energy is extracted, converting fluid energy into usable work. The efficiency of these devices plays a crucial role in determining how effectively they convert mechanical energy into fluid energy or vice versa.
Examples & Analogies
Think of a waterwheel at a mill: it captures the energy from flowing water (turbine function) to grind wheat into flour, whereas a swimming pool pump uses energy to circulate water (pump function). The efficiency of both affects how much work they can effectively accomplish.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic Gradient Line: Indicates the pressure head in fluid systems.
-
Energy Gradient Line: Represents the total mechanical energy including both potential and kinetic components.
-
Efficiency in Pumps: Refers to how well a pump converts mechanical energy into fluid energy.
-
Turbines: Machines that extract mechanical energy from moving fluids, lowering their pressure.
-
Bernoulli's Equation: Mathematical expression of energy conservation in fluid flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of measuring hydraulic gradients in a pipe using piezometers.
-
Using Bernoulli's equation to calculate pressure differences between two points in fluid flow.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Pumps make the water rise high, Turbines let the power fly.
📖 Fascinating Stories
-
Imagine a bustling town where pumps push water to the tops of buildings, making life possible, while turbines in the river glide silently, extracting energy from the flowing water to power the town's lights.
🧠 Other Memory Gems
-
P.E.T. (Pressure, Energy, Turbines) helps remember components of fluid energy.
🎯 Super Acronyms
H.E.E. (Hydraulic, Energy, Efficiency) summarizes the core ideas in managing fluid systems.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Gradient Line
Definition:
A line that represents the energy height of fluid due to pressure, coinciding with the liquid's free surface in open channel flow.
-
Term: Energy Gradient Line
Definition:
A line that represents the total mechanical energy—potential and kinetic—of a fluid.
-
Term: Mechanical Energy
Definition:
The energy associated with the motion and position of an object, critical in fluid systems for transferring and transforming energy.
-
Term: Efficiency
Definition:
The ratio of useful output energy to the input energy, indicating how well a system converts energy.
-
Term: Bernoulli's Equation
Definition:
An equation that describes the conservation of energy in flowing fluids, relating pressure, velocity, and elevation.