Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Hydraulic Gradient Lines
Unlock Audio Lesson
Today, we'll start with hydraulic gradient lines. Who can tell me what a hydraulic gradient line indicates in an open channel flow?
Is it the level of the fluid's free surface?
Exactly! The hydraulic gradient coincides with the free surface because there’s no pressure head. It's essential in recognizing how water flows in channels.
How does this relate to energy gradient lines?
Great question! The energy gradient line adds the velocity head above the free surface, showing how kinetic energy affects flow. Remember the acronym HEAL: Hydraulic Equals Atmospheric Level—this can help you remember the relationship!
What about the case of pipes? Do we measure these gradients differently?
Yes! In pipes, we use devices like piezometers and Pitot tubes to measure pressure and velocity, allowing us to calculate these gradients effectively.
So hydraulic gradient lines change depending on the system?
Correct! The context—whether open channel or pipe—affects how we interpret and measure the hydraulic gradient.
Mechanical Energy Losses
Unlock Audio Lesson
Now, let's talk about mechanical energy losses in a system. Can anyone explain what happens to energy as fluids flow?
Energy decreases due to friction, right?
Exactly! This energy loss is a key consideration, which shows mechanical energy transitions to thermal energy. Remember the mnemonic FATE: Friction Affects Total Energy.
Why do we care about this in designs?
Understanding energy loss helps engineers design efficient systems by minimizing these losses. We'll analyze this further when discussing turbines!
Pumps and Turbines
Unlock Audio Lesson
Let's dive into pumps and turbines! Who can tell me the role of a pump in a fluid system?
A pump adds energy to the fluid by increasing its pressure.
Well done! Pumps transform mechanical energy into fluid energy. What about turbines?
Turbines do the opposite—they extract energy from the fluid?
Correct! Turbines convert fluid energy into mechanical energy, reducing fluid pressure. Think of the acronym PUT: Pumps Up, Turbines down.
How does this impact overall efficiency?
Fantastic question! Both device efficiencies must be calculated to design optimal systems, integrating all energy loss factors.
Bernoulli's Equation
Unlock Audio Lesson
Now that we've discussed pumps and turbines, let's connect to Bernoulli's equation. Can anyone define it?
Isn’t it about the conservation of energy in flowing fluids?
Exactly! It relates pressure, velocity, and height. Remember the phrase 'Energy in equals energy out.' Who can recall the three energy components in Bernoulli's Equation?
Kinetic, potential, and pressure energy!
Correct! Kinetic energy relates to velocity, potential to elevation, and pressure to fluid statics. This is why it's so vital for analyzing flow systems!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into power calculations within fluid systems, distinguishing between hydraulic and energy gradient lines in open channel flow and pipe flow. We explore mechanical energy transformations in pumping and turbine systems and illustrate these concepts through Bernoulli's equations, examples of flow analysis, and real-world applications.
Detailed
Power Calculations
This section explores the fundamentals of power calculations in fluid mechanics, focusing on understanding hydraulic and energy gradient lines, the transformative roles of pumps and turbines, and the implications of mechanical energy losses.
Key Points:
- Hydraulic and Energy Gradient Lines: In open channel flow, the hydraulic gradient coincides with the free surface of the liquid, while head loss due to friction causes the energy gradient line to slope downward.
- Pressure Changes: The atmospheric pressure at the pipe exit influences the hydraulic gradient, leading to variations in gauge pressure along the flow.
- Mechanical Energy Transformations: Pumps increase mechanical energy in fluid systems by raising pressure, whereas turbines extract mechanical energy and drop pressure, leading to energy losses in the system.
- Bernoulli’s Equation: This equation serves as a foundation for analyzing fluid flow and power calculations, linking changes in kinetic and potential energy to pressure differentials in fluid systems.
- Practical Applications: Utilizing theoretical and actual conditions, the section connects practical calculations to broader concepts regarding energy efficiency and flow systems.
Through these discussions, students gain insight into how to analyze and calculate power within fluid systems while appreciating the interconnectedness of hydraulic principles.
Youtube Videos
![Power and Energy: Example 1: Part 1 [Fluid Mechanics #32]](https://img.youtube.com/vi/6PM15ec7oMs/mqdefault.jpg)
![Power and Energy Equation [Fluid Mechanics #31]](https://img.youtube.com/vi/l5wWVKOGm6Y/mqdefault.jpg)
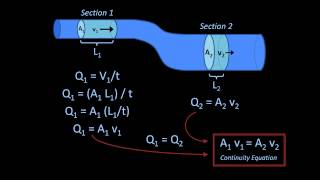
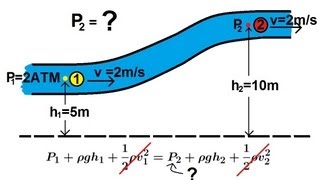
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Open Channel Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In open channel flow, the hydraulic gradient lines coincide with the free surface of the liquid because there is no pressure head. The energy gradient lines include the velocity head above the free surface.
Detailed Explanation
In open channel flow, the water flows without any pressure exerting from above, which means the point where the water meets the air is the reference for the hydraulic gradient. This leads to the understanding that any energy gradient would contain the velocity head, which is the kinetic energy of the flowing water moving above the free surface. Essentially, this relationship helps visualize how water moves in channels without being confined by pressure.
Examples & Analogies
Imagine a river flowing downhill. The surface of the river represents the hydraulic gradient. As water flows faster, it creates more energy, much like how a cyclist speeds up downhill. The height of the cyclist on the hill would represent the water's potential energy before it starts flowing, while the speed equates to kinetic energy during the descent.
Pressure Head in Pipes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In pipe flow, a piezometer measures the hydraulic gradient line. The pressure head becomes atmospheric when flow exits a pipe, making the hydraulic gradient line coincide with the pipe outlet.
Detailed Explanation
When water is flowing through a pipe and exits, the pressure exerted by the water decreases until it reaches atmospheric pressure. The piezometer is a device used to measure the fluid pressure within the pipe, indicating where the pressure level stands in relation to the external atmospheric pressure. This can help engineers determine how much energy remains in the system at various points along the flow.
Examples & Analogies
Consider a garden hose. When you let water flow out from the end of a hose, the water pressure drops as it exits into the air, just like in a pipe. The pressure inside the hose can be thought of as being measured by a piezometer, reflecting how much energy (or force) the water has within the hose versus when it freely flows out.
Mechanical Energy Losses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mechanical energy losses due to friction cause the energy gradient line and hydraulic gradient line to slope downwards in the direction of flow. Energy losses are inevitable in flow systems.
Detailed Explanation
As water flows through any system, it encounters resistance from surfaces and bends, leading to a decrease in energy known as mechanical energy loss. This loss creates a gradient where the hydraulic and energy gradient lines slope downwards along the direction of flow, indicating that energy is being dissipated and cannot be entirely converted into useful work.
Examples & Analogies
Picture sliding down a slide at a playground. You might start at a high point (potential energy), but as you go down, friction against the slide reduces your speed (energy loss). Eventually, you reach the bottom with less energy than when you started, illustrating how energy dissipates in real-life scenarios.
Power Generation from Pumps and Turbines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Pumps increase mechanical energy in the fluid by raising pressures, while turbines extract mechanical energy from the fluid by reducing pressures. Power can be calculated as the energy input per unit time.
Detailed Explanation
In fluid mechanics, pumps and turbines are critical components. Pumps add energy to a fluid, thus increasing its pressure and moving it to higher elevations or onto other systems. Conversely, turbines harvest energy from flowing fluids, converting it back to useful work - here, pressure decreases as energy is extracted. The overall power output can be evaluated based on the energy added or subtracted over a given time period.
Examples & Analogies
Think of a waterwheel at a mill. The wheel works like a turbine – as water flows over it, the kinetic energy of the water turns the wheel and generates power, which can then be harnessed to grind grain. Similarly, when you pump water to a higher tank, you’re adding energy with a pump, preparing it for use either for irrigation or water supply.
Efficiency of Fluid Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mechanical efficiency can be quantified as the ratio of output power to input power. Understanding this helps to measure how effectively systems convert energy.
Detailed Explanation
Efficiency in fluid systems highlights how well energy is utilized during processes, such as pumping and energy recovery. It is a critical measure to understand losses occurring in machines in terms of energy conversion. Higher efficiencies indicate better performance, while lower efficiencies highlight areas that require improvement.
Examples & Analogies
Consider a car engine. The fuel you put in is the energy input, and the car's ability to move is the output. If the engine transforms most of that fuel into movement efficiently, it is considered high on the efficiency scale. If a lot of fuel is wasted, the efficiency drops, showing how much energy is lost to heat, sound, or other forms.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic and Energy Gradient Lines: These lines show the relationship between pressure, velocity, and elevation in fluid flow systems.
-
Mechanical Energy Loss: Energy losses due to friction and turbulence impact the efficiency of fluid systems.
-
Pumps and Turbines: Devices that convert energy types; pumps add energy while turbines extract it.
-
Bernoulli's Equation: A principle that describes the balance of energy in flowing fluids.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The pressure at the exit of a pipe is atmospheric pressure, influencing the flow rate due to hydraulic gradient lines.
-
In a pump, the energy supplied is transformed into fluid energy, increasing the system's pressure.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Up the pump goes, energy in flow, down with the turbine, watch it go slow.
📖 Fascinating Stories
-
Once upon a time, in a land of flowing rivers, a pump helped water rise high to help crops thrive, while a turbine turned the wheels of a mill, taking energy low, by releasing pressure still.
🧠 Other Memory Gems
-
HEAL: Hydraulic Equals Atmospheric Level to remember the hydraulic gradient!
🎯 Super Acronyms
PUT
- Pumps Up
- Turbines Down to describe their functions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Gradient Line
Definition:
A line that indicates the fluid's potential energy due to elevation in open channel flow, coinciding with the free surface.
-
Term: Energy Gradient Line
Definition:
A line that represents the total mechanical energy of the fluid, including kinetic and potential energy.
-
Term: Mechanical Energy Losses
Definition:
The loss of energy in a fluid system mainly due to friction and turbulence.
-
Term: Pump
Definition:
A device that increases the pressure and energy of a fluid, transforming mechanical energy into fluid energy.
-
Term: Turbine
Definition:
A machine that converts fluid energy into mechanical energy, reducing fluid pressure.