Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Efficiency
Unlock Audio Lesson
Today, we will discuss motor and generator efficiency. Can anyone tell me what efficiency means in this context?
Isn't it about how well a machine converts energy from one form to another?
Exactly! Efficiency is a measure of how much input energy is converted into useful output energy. For motors, it's electrical to mechanical energy, and for generators, it's the opposite. Remember the acronym ME = PE, where Mechanical Energy equals Potential Energy converted.
What are some factors that affect these efficiencies?
Great question! Factors include friction losses, heat losses, and the design of the system itself.
Let's summarize: Efficiency compares output power to input power in mechanical systems.
Energy Gradient Lines
Unlock Audio Lesson
Next, let's look at hydraulic gradient lines. These lines represent the energy available to the fluid in a hydraulic system. Can someone describe what energy gradient lines are?
I think they include not just pressure energy but also kinetic energy?
Correct! Energy gradient lines add velocity head to the hydraulic gradient line. Think of it as a visual representation of how energy is distributed across a pipe system.
How do we determine these lines in a real-world application?
In practice, you can use devices like piezometers to measure pressure along the system. Let's keep this in mind when we discuss energy losses next.
To summarize today's concept, hydraulic lines indicate potential for energy based on height, while energy gradient lines indicate actual energy, including kinetic factors.
Mechanical Energy Losses
Unlock Audio Lesson
Now, let's understand energy losses. What happens to energy as fluids travel through pipes?
It decreases due to friction and turbulence, right?
Yes! These losses cause a decline in the hydraulic gradient line. The greater the friction, the lower the energy output.
So how do pumps and turbines fit into this?
Pumps increase pressure, converting mechanical energy to fluid energy, while turbines extract energy from the fluid flow. Always remember that both processes incur losses.
In summary, mechanical energy losses occur due to friction as fluids move, which directly impacts system efficiency.
Calculating Efficiency
Unlock Audio Lesson
Let's calculate efficiency. What is the formula for efficiency?
It’s the output power divided by input power, right?
Exactly! Let's say a motor has an input power of 100 watts and an output power of 80 watts. What is its efficiency?
That would be 80 divided by 100. So, 0.8 or 80% efficiency?
Well done! Remember, the higher the percentage, the more efficient the system.
To recap, efficiency is calculated as output divided by input, and helps us quantify performance.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Motor and generator efficiency is essential for understanding energy conversion in systems involving pumps and turbines. The section discusses hydraulic and energy gradient lines, energy losses due to friction, and the factors affecting efficiency in mechanical systems.
Detailed
Motor and Generator Efficiency
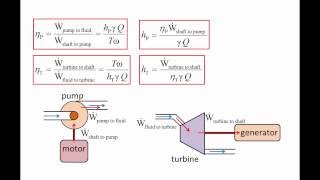
In this section, we delve into the concepts of motor and generator efficiency within fluid systems, particularly in relation to pumps and turbines. Motor efficiency is defined as the ratio of mechanical power output to electrical power input, while generator efficiency is the ratio of electrical power output to mechanical power input.
Key to understanding these efficiencies is the consideration of energy losses, primarily due to friction, heat, and other factors that result in mechanical energy dissipation. When fluid flows through a system, mechanical energy can be lost, causing the hydraulic gradient line to decline in accordance with the direction of flow. Furthermore, hydraulic and energy gradient lines illustrate the behavior of fluids within pipelines, helping to visualize how pressure and velocity influence overall energy conservation.
Understanding these principles is vital for optimizing systems in engineering applications, such as in hydropower projects, where maximizing the conversion of energy is paramount.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Pump and Turbine Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us consider the problems when we generally use as engineers having a pump and turbine systems. As you know it, the pump is transferring mechanical energy to fluid by rising pressures. So, fluid gains energy because of the pumping systems by rising its pressures. In a similar way, the turbine does the opposite, extracting mechanical energy from the fluid by dropping its pressure.
Detailed Explanation
Pumps and turbines are essential components in fluid systems. A pump works by adding energy to a fluid, causing an increase in pressure. This process allows the fluid to move to higher elevations or to flow through a system against resistance. Conversely, a turbine extracts energy from the fluid, usually in a hydropower context, and this happens when the fluid passes through the turbine, causing it to spin and lower the fluid's pressure.
Examples & Analogies
Think of a pump like a bicycle pump. When you push down on the pump handle, you're increasing the pressure inside the pump, forcing air into a tire. Conversely, a turbine can be likened to a windmill; as the wind (the fluid) flows past the blades, it slows down while turning the blades, converting that energy into mechanical work.
Energy Losses in Fluid Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Whenever we have a system, there is energy losses. We cannot convert total mechanical energy entirely from pump or turbine due to heat energy losses, sound energy losses, and other forms of energy loss. Because of that, there is an efficiency associated with these systems.
Detailed Explanation
In any mechanical system, some energy is inevitably lost due to various factors such as friction, turbulence, and heat generation. This means that not all of the energy provided by the pump or turbine is effectively converted into useful work. Instead, only a portion of it contributes to the desired outcome, leading to the concept of efficiency, which is defined as the ratio of useful output energy to input energy.
Examples & Analogies
Imagine pouring water into a leaky bucket. Even though you pour in a certain amount of water (input energy), some of it leaks out (energy loss), and only the water that remains in the bucket represents the useful output energy. The efficiency of this process would be the amount of water left in the bucket compared to what you initially poured in.
Calculating Efficiency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If we say efficiency equals 1, it means that whatever input we get, the output is the same. This quantification of mechanical efficiency can be expressed in terms of loss as well. We can represent the efficiency of pumps and turbines as a ratio of output to input.
Detailed Explanation
Efficiency is typically expressed as a percentage and is calculated using the formula: Efficiency = (Output Power / Input Power) x 100%. For example, if a pump uses 100 units of energy (input) and delivers 90 units of energy, the efficiency would be 90%. This measurement helps engineers determine how well the pump performs relative to its energy consumption.
Examples & Analogies
Think about a light bulb. If it uses 60 watts of power but only produces light worth 50 watts due to heat loss, its efficiency is about 83%. This is similar to how we evaluate the performance of motors and pumps in a system, ensuring that we choose the most efficient options.
Motor and Generator Efficiency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Similar to pumps and turbines, motors and generators also have efficiencies that depend on their performance. Motors convert electrical power into mechanical power, while generators convert mechanical power into electrical power.
Detailed Explanation
Both motors and generators have efficiencies that indicate their performance in converting one form of energy to another. The efficiency of a motor can be calculated by comparing its mechanical output power to the electrical input power, while the efficiency of a generator compares its electrical output power to the mechanical input power. High efficiency means less energy wasted.
Examples & Analogies
Consider an electric fan. When you switch it on, electrical energy is supplied to the motor, which converts it into mechanical energy to spin the blades. If the fan uses 50 watts of electrical power but only moves air effectively equivalent to 40 watts of mechanical power, its efficiency is 80%. Understanding these efficiencies helps us choose devices that waste the least energy.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Efficiency: The ratio of useful power output to total power input in motors and generators.
-
Hydraulic Gradient Line: Represents the potential energy in a fluid system.
-
Energy Gradient Line: Includes both hydraulic and kinetic energy of the fluid.
-
Mechanical Energy Loss: Energy that dissipates primarily due to friction in fluid systems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A motor with an electrical input of 200 watts producing 160 watts output has an efficiency of 80%.
-
A turbine that converts 1000 watts of fluid energy into 850 watts of mechanical output has an efficiency of 85%.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If motors turn watts into might, the higher the efficiency, the brighter the light!
📖 Fascinating Stories
-
Imagine a pump as a happy worker, lifting water high while losing little energy to friction, making its boss proud of its efficiency!
🧠 Other Memory Gems
-
Remember 'ME is PE' - Mechanical Energy is Potential Energy for understanding fluid systems.
🎯 Super Acronyms
HELM = Hydraulic Energy Loss Mechanism, to remember factors draining energy in fluids.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Motor Efficiency
Definition:
The ratio of mechanical power output to electrical power input in motor systems.
-
Term: Generator Efficiency
Definition:
The ratio of electrical power output to mechanical power input in generator systems.
-
Term: Hydraulic Gradient Line
Definition:
A line that represents the potential energy available to the fluid due to elevation or pressure.
-
Term: Energy Gradient Line
Definition:
A line indicating total energy, including both hydraulic and velocity head.
-
Term: Mechanical Energy Losses
Definition:
Energy losses in a system due to friction, turbulence, and other factors, which reduce efficiency.