Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Hydraulic Gradient Lines
Unlock Audio Lesson
Welcome everyone! Today, we begin with hydraulic gradient lines. Can anyone tell me what they know about hydraulic gradient lines in the context of open channel flow?
I think they represent the energy level of the fluid, right?
That's partially correct! The hydraulic gradient line coincides with the free surface of the liquid in open channel flow. This means there is no pressure head present. So what does that imply for the flow?
Does that mean the hydraulic gradient line is at the same level as the water surface?
Exactly! The hydraulic gradient line aligns with the water surface because it solely represents the elevation head due to the lack of pressure head. Let's remember it with the acronym HGL—Hydraulic Gradient Level.
What about energy gradient lines? How are they different?
Good question! Energy gradient lines include velocity head in the calculation. So, while the hydraulic gradient line is at the free surface, the energy gradient line is slightly above since it adds in the velocity component. Any thoughts on why this is important?
I guess it shows how much energy is present in the flow, which would affect how fluid moves through a system.
Exactly! Of course, this is critical when evaluating system performance.
Energy Losses and Mechanical Systems
Unlock Audio Lesson
Now let's discuss energy sources in fluid systems—specifically, pumps and turbines. How does a pump affect energy in a fluid system?
It raises the pressure, right?
Exactly! Pumps convert mechanical energy to fluid energy by increasing the pressure. Can anyone tell me how this relates to our earlier discussion about energy gradient lines?
It would cause the energy gradient line to rise since the pressure is higher?
Correct! Now, what about turbines? What role do they play?
They lower the pressure by extracting energy, right?
Yes, they convert fluid energy back into mechanical energy, which lowers pressure in the system. This can lead to a downward slope in both hydraulic and energy gradient lines as energy is lost due to friction along the way. Remember, the pump can increase the gradient while the turbine can decrease it. Let's use the mnemonic 'Pumps Push, Turbines Take!' to recall this easily.
That's helpful!
Pressure Head and Energy Grade Lines
Unlock Audio Lesson
Now, who can explain how the pressure head relates to the hydraulic gradient line?
When pressure head is zero, does that mean the hydraulic gradient line intersects the free surface?
Exactly! If the pressure head is atmospheric, then the hydraulic gradient line aligns with the fluid's free surface. What about when the pressure increases?
Then the hydraulic gradient line would be higher than the free surface, right?
Yes! This information is crucial for analyzing fluid systems. A quick fact to remember: when we represent the energy gradient line, it's always above the hydraulic gradient line because of the velocity term—this helps in visualizing how energy behaves in flow systems.
So, if we observe both lines, we can assess the energy available at various points along the flow?
Yes, spot on!
Practical Applications
Unlock Audio Lesson
Let's now discuss how all of this knowledge can be applied in real engineering scenarios. Who can give me an example of where these principles might be important?
In hydropower plants! We need to manage how water flows to generate electricity.
Exactly! In these systems, understanding the difference in hydraulic and energy gradient lines helps engineers design effective systems. What challenges might arise?
Maybe friction losses that can affect efficiencies?
Right! Friction losses will modify our calculations for energy efficiency and system performance. Remember the last mnemonic we mentioned: 'Pumps Push, Turbines Take!' These concepts directly impact efficiency and energy output in such applications.
This connects all the theory to practice!
Absolutely! Always link concepts back to their application.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains how hydraulic gradient lines coincide with free surfaces in open channel flows and how they are represented differently in closed pipe systems. It further delves into the mechanical energy differences introduced by pumps and turbines, as well as the implications of pressure changes along these gradients.
Detailed
Energy Gradient Lines
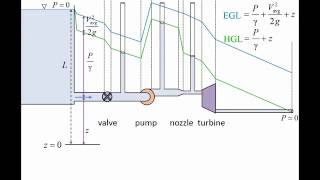
In fluid dynamics, understanding energy gradient lines is key to analyzing fluid flows in both open channels and enclosed piping systems. Hydraulic gradient lines are defined as coinciding with the free surface of liquid under open channel conditions because there is no pressure head. The energy gradient line, however, incorporates the velocity head above this free surface.
For closed systems, such as pipes, hydraulic gradient lines can be measured using piezometers. As fluid exits a pipe, the hydraulic gradient aligns with atmospheric pressure, indicating that the pressure head is effectively zero. In contrast, energy losses due to friction cause both the hydraulic and energy gradient lines to slope downward in the direction of flow.
Mechanical energy is introduced or extracted from fluid systems through pumps and turbines, which raise and reduce pressure, respectively. This section also highlights the importance of understanding the relationships between pressure heads, velocity heads, and energy flows in determining the efficiency of fluid systems, such as the functionality of turbines and pumps. Intricacies around gauge pressure and energy losses are vital to effectively managing fluid flow in engineering applications.
Youtube Videos
![Hydraulic and Energy Grade Line ? with animation [ HGL and EGL ]](https://img.youtube.com/vi/moI4DQNirAw/mqdefault.jpg)
![Fluid Dynamics -2 [Bernoulli's principle, total energy line and Hydraulic gradient line, pitot tube]](https://img.youtube.com/vi/HGsYXbjW5qA/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Hydraulic Gradient in Open Channel Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In open channel flow, the hydraulic gradient lines coincide with the free surface of the liquid because there is no pressure head. The water surface represents the hydraulic gradient line.
Detailed Explanation
In open channel flow, we can observe that the hydraulic gradient line is equivalent to the free surface of the liquid. This is due to the absence of a pressure head, which means that the surface of the water directly represents the hydraulic gradient. The energy gradient line, however, includes the velocity head, which is an additional component of energy related to the speed of the water above the free surface.
Examples & Analogies
Think of a river or a stream where the surface of the water indicates how high the water is if you were to measure it with a ruler. In this case, the height of the water represents the hydraulic gradient. If you were to throw a stone into the water and it causes ripples, the velocity of these ripples includes more energy than just the height of the water.
Functions of Pipes vs Channels
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In pipes, we can use a piezometer to measure hydraulic gradient lines, and a pitot tube to measure energy gradient lines. When fluid exits a pipe into the atmosphere, the pressure head becomes atmospheric pressure.
Detailed Explanation
When we use pipes instead of open channels, we can utilize instruments like piezometers to directly measure the hydraulic gradient. This is because pipes can maintain pressure within the liquid, unlike open channels. Additionally, for measuring energy gradient lines, a pitot tube is employed to account for the pressure and velocity of the fluid. When a fluid exits a pipe, the pressure transforms into atmospheric pressure, similarly to how it does at the surface of an open channel.
Examples & Analogies
Imagine a garden hose connected to a water source. When you turn the tap, water comes out under pressure (which can be measured with a piezometer) and when you remove the hose from the tap, the water flows freely into the air much like how it flows in an open channel.
Mechanical Energy Losses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mechanical energy losses due to friction cause the energy gradient lines to slope downward in the direction of flow. Energy losses will cause both energy gradient lines and hydraulic gradient lines to show a downward trend.
Detailed Explanation
As water flows through a pipe, it experiences friction against the walls of the pipe. This friction causes losses in mechanical energy, resulting in a gradual downward slope for both the energy gradient line and the hydraulic gradient line in the direction of flow. While energy gradients generally decline due to these losses, the hydraulic gradient may not always show the same downward trend, depending on the system's configuration.
Examples & Analogies
Consider a water slide at an amusement park. As the water slides down from a height, it loses speed due to friction with the slide's surface, similar to how a fluid loses energy in a pipe due to friction. The energy is being converted to heat, just like how you might warm your hands after rubbing them together.
Pressure Measurements and the Gradient Relationship
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In relation to the hydraulic gradient line, gauge pressure above the line is negative, while below the line is positive. This difference is critical when analyzing flow systems in pipes.
Detailed Explanation
The hydraulic gradient line serves as a reference point. When a pressure measurement is above this line, the gauge pressure is negative, indicating under-pressure compared to atmospheric pressure. Conversely, if the measurement is below the hydraulic gradient line, the gauge pressure is positive. This distinction is important when addressing the dynamics of piping systems and how pressure influences fluid behavior at various points in the system.
Examples & Analogies
Think of using a barometer to measure air pressure. If the pressure reading indicates lower pressure than the atmospheric level, it can be seen as a negative pressure context, similar to how a vacuum works. Conversely, too much pressure would give a positive reading, informing us how much force is exerted on the system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic Gradient Line: Represents the elevation of the liquid's free surface in open channels.
-
Energy Gradient Line: Incorporates energy due to elevation and velocity above the hydraulic gradient line.
-
Pressure Head: The vertical height of a liquid column due to pressure, impacting the flow.
-
Mechanical Energy Losses: Loss of energy through friction during fluid movement, which can affect efficiency.
-
Bernoulli's Equation: Fundamental equation allowing calculation of pressure, velocity, and energy at different points in fluid flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a dam system, the energy gradient lines modify based on the velocity of water flowing through turbines, affecting overall energy output.
-
In a city water distribution system, understanding hydraulic gradient lines helps engineers ensure adequate pressure and flow rate at endpoints.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When water's free, the line above, is where the gradient loves to shove.
📖 Fascinating Stories
-
Imagine a fluid flowing through varying landscapes, where pumps lift it high like heroes while turbines help it drop down low, managing energy all the way.
🧠 Other Memory Gems
-
Pumps Push, Turbines Take - remember two sources for energy to make!
🎯 Super Acronyms
HGL for Hydraulic Gradient Line, an easy way to remember the line.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Gradient Line
Definition:
The line representing the elevation of the liquid's free surface or the potential energy in an open channel flow.
-
Term: Energy Gradient Line
Definition:
The line that represents the total energy of the fluid flow, including potential energy from elevation and kinetic energy from velocity.
-
Term: Pressure Head
Definition:
The height of fluid column due to pressure in a system, reflected as part of the hydraulic gradient.
-
Term: Velocity Head
Definition:
The potential energy of a fluid due to its velocity, often used in calculations of energy gradient lines.
-
Term: Mechanical Energy Losses
Definition:
Energy lost due to friction and other factors as fluid flows through a system, impacting overall efficiency.
-
Term: Bernoulli's Equation
Definition:
A fundamental equation in fluid mechanics that describes the conservation of energy in flowing fluids.
-
Term: Hydropower
Definition:
The production of electricity through the movement of water, often dependent on understanding fluid dynamics.