Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Gradient Lines
Unlock Audio Lesson
Today, let's start by understanding what hydraulic gradient lines are. In open channel flow, they coincide with the liquid's free surface. Can anyone explain why that is?
Because there's no pressure head in open channels?
Exactly! In open channels, since only gravity acts on the fluid, the hydraulic gradient is simply the elevation of the water surface. Now, can someone tell me how energy gradient lines relate to this?
It includes the velocity head above the free surface, right?
Correct! To remember that, think of it as VE: Velocity Energy!
So, in pipes, we need different instruments to measure these gradients, like piezometers and pitot tubes?
Exactly! Great connections! The energy gradient line in pipes takes pressure head into account, unlike open channels.
Flow Direction and Pressure Relationships
Unlock Audio Lesson
Now, let’s discuss how flow direction affects gradient lines. When we have flow exiting a pipe, what happens at the outlet?
The pressure head becomes atmospheric pressure, making the hydraulic gradient equal to that outlet?
Exactly! This means the hydraulic gradient line and the pipe outlet coincide, making it easier to model our systems!
But what about energy losses in these systems?
Good question! Friction losses transform mechanical energy into heat, causing downward slopes in both hydraulic and energy gradient lines. Remember: 'Energy Down = Losses Up!'
Pumps and Turbines
Unlock Audio Lesson
Let’s now look at pumps and turbines. What does a pump do in a fluid system?
It adds mechanical energy to the fluid by increasing pressures.
Exactly! Think of it as 'pumping up' the fluid! And what about turbines?
They extract mechanical energy from the fluid, decreasing its pressure.
Right! Remember, 'Turbines Tear Down, Pumps Build Up.' Now, let’s analyze the efficiency of these systems. How would you calculate it?
By finding the ratio of input mechanical energy to output energy?
Correct! Efficiency helps us quantify how well our systems convert energy.
Real-World Applications
Unlock Audio Lesson
In real-world applications, understanding these concepts matters greatly. For example, how do we use our understanding of energy gradients in designing a dam?
We would account for the energy gradients to ensure optimal flow and energy capture?
Yes! Ensuring sufficient mechanical energy translates to efficient electricity generation! Now, let’s summarize what we’ve discussed so far.
Today we covered gradient lines, flow relationships, pumps, and their efficiencies, emphasizing their real-world implications, especially in engineering applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the principles governing hydraulic gradient lines and energy gradient lines are discussed in connection with open channel flow and pipe systems. It emphasizes the significance of pumps and turbines in mechanical energy transfer and introduces concepts of efficiency in energy systems, including practical examples and problems.
Detailed
Combined Efficiency of Systems
This section focuses on understanding key concepts related to hydraulic and energy gradient lines in different fluid flow systems, particularly in open channels and pipe networks. The hydraulic gradient in open channels coincides with the free surface of the liquid since pressure heads are absent, while the energy gradient takes into account velocity heads. In contrast, pipes involve measurement instruments like piezometers and pitot tubes for assessing these gradients due to the presence of pressure heads.
It also explains how the exiting flow from pipes implies atmospheric pressure at the outlet, reiterating that mechanical energy losses due to friction lead to a decline in both hydraulic and energy gradient lines along the flow direction. The section further elaborates on pumps and turbines, highlighting their functions of increasing and decreasing mechanical energy in fluid systems, respectively.
Key concepts such as efficiency in mechanical energy systems, energy losses, and real-world applications in hydraulic engineering are presented through practical problems, ultimately underscoring the significance of understanding energy dynamics in fluid systems for effective engineering design.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Hydraulic and Energy Gradient Lines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And okay, we are not discussing about open channel flow heads, but in case of open channel flow, the hydraulic gradient lines coincides with the free surface of the liquid okay. Because there is no pressure head. So, whatever the water surface free surface, that what will be hydraulic gradient line and the energy gradient lines will have a included the velocity head above the free surface.
Detailed Explanation
In open channel flow, such as rivers or ditches, the hydraulic gradient line is the same as the water's free surface. This is because there is no pressure head exerted above the water surface, which is typically present in closed pipes. The energy gradient line, on the other hand, adds velocity head to the hydraulic gradient. Essentially, the velocity head represents the kinetic energy of the fluid above the free surface.
Examples & Analogies
Imagine a river where the flowing water represents the free surface. As you stand by the bank, the river's height shows you the hydraulic gradient. When a leaf floats on the surface, its fast movement upstream can be likened to the velocity head, indicating that some energy is present due to that motion.
Pressure and Energy Gradient Lines in Pipes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But in case of the pipes, we can have a piezometer to measure it, what could be the hydraulic gradient lines. Energy gradient line to measure it we need to have a pitot tube to compute what will be these things.
Detailed Explanation
In piping systems, the hydraulic gradient is different because pressure can be measured using a device known as a piezometer. This allows engineers to directly assess how the pressure changes along the pipe. To evaluate the energy gradient line, a pitot tube is necessary, as it helps measure the velocity of the fluid and thus calculate the energy associated with that velocity.
Examples & Analogies
Think of a garden hose. If you stick a gauge on the hose, you can measure how much pressure is inside it—this is akin to using a piezometer. If you have a small tube that sticks into the flowing water inside the hose and catches the water, much like a pitot tube, you can see how fast the water is actually flowing out, thus giving you insights into the kinetic energy of the water.
Mechanical Energy Losses in Flow Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mechanical energy losses due to the frictional effects, which is converting from thermal energy, the causes the energy gradient line, hydraulic gradient line, to a slope downwards in the directions of the flow.
Detailed Explanation
As water flows through pipes, it experiences friction, much like how rubbing your hands together creates heat. This friction causes energy to be lost from the system, resulting in a downward slope of both the energy gradient line and the hydraulic gradient line. This represents that not all mechanical energy is conserved due to losses.
Examples & Analogies
Consider sliding down a slide at the park. If the slide is rough, you feel less speed than if it were smooth because some of your energy is lost to friction against the slide. Similarly, in a pipe, energy is consumed in overcoming friction, causing pressure and energy loss.
Pump and Turbine Functionality
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
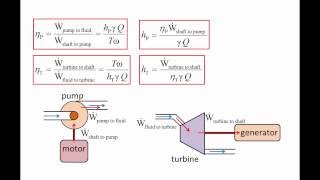
As you know, the pump is transfer from mechanical energy to fluid by rising pressures. Fluid gains the energy because of the pumping system by rising its pressures. The turbine does opposite things, that it takes out or extract the mechanical energy from the fluid by dropping its pressure.
Detailed Explanation
In hydraulic systems, pumps add energy to fluids by increasing their pressure, effectively aiding fluid transport. Conversely, turbines extract energy from flowing fluids, converting it into usable mechanical energy, which lowers the fluid's pressure in the process. This relationship is crucial for understanding how mechanical energy is used and transformed in fluid systems.
Examples & Analogies
Picture a bicycle pump: as you push down on the pump, you are forcing air into a tire, raising its pressure. This is like how a pump increases fluid energy. Now, think of a water wheel at a mill. As water flows past, it moves the wheel, converting water energy into mechanical energy to grind grain, akin to what happens in a turbine.
Assessing Overall Efficiency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Whenever we have a system, there is energy losses. We cannot convert total mechanical energy entirely from mechanical pump or pump. There will be some heat energy losses, the sound energy losses, will have the energy losses from that. Because of that, there is an efficiency looped to that.
Detailed Explanation
Despite the ideal situation where pumps and turbines are assumed to be 100% efficient, real-world applications always involve energy losses due to friction, heat, and other factors. Understanding the efficiency ratio of input to output helps in evaluating system performance and making necessary adjustments to improve operation.
Examples & Analogies
Think about your phone charger: while it efficiently charges your phone, some energy is lost as heat during the process. If the charger is very efficient, it will warm up only slightly. To track how well it's performing, you consider how much energy it draws versus the energy that actually reaches the phone.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic Gradient: Defined by the free surface in open channels without pressure head.
-
Energy Gradient: Represents total energy in the system, including velocity head.
-
Pumps: Increase mechanical energy by raising fluid pressure.
-
Turbines: Extract mechanical energy, decreasing fluid pressure.
-
Efficiency: Ratio that defines how well an energy system converts input to output.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An open channel where the hydraulic gradient line corresponds to the water surface, indicating no pressure head.
-
A turbine generating electricity from flowing water effectively by translating hydraulic energy into mechanical work.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In channels wide, the gradient's high, / Energy flows as the waters fly.
📖 Fascinating Stories
-
Imagine a river where the water flows over rocks; the pressure drops, and energy is lost each time it shocks.
🧠 Other Memory Gems
-
Pumps Push (add pressure), Turbines Take (extract energy).
🎯 Super Acronyms
PET
- Pumps Enhance
- Turbines Extract.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Gradient Line
Definition:
A line representing the height of water in an open channel, indicating pressure equal to atmospheric.
-
Term: Energy Gradient Line
Definition:
A line indicating the total energy (including velocity head) in a fluid system.
-
Term: Pump Efficiency
Definition:
The ratio of useful energy output from a pump to the energy input, expressed as a percentage.
-
Term: Turbine Efficiency
Definition:
The measure of how effectively a turbine converts fluid energy to mechanical work.
-
Term: Mechanical Energy Losses
Definition:
Energy losses incurred due to friction and turbulence in flowing fluids.