Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Venturi Tubes
Unlock Audio Lesson
Welcome class! Today we will cover Venturi tubes and how they function based on changes in fluid flow dynamics. Can anyone tell me what a Venturi tube is?
Isn't it a device used to measure the flow rate of liquids?
Exactly! It measures fluid flow by utilizing the principle of Bernoulli's equation. This relationship of pressure and flow rates allows us to derive mass flux. Can anyone define what Bernoulli's equation states?
It relates the pressure, kinetic energy, and potential energy in a flowing fluid.
Correct! We often simplify the flow conditions to one-dimensional, steady, and incompressible, enhancing calculations. Remember, pressure and velocity are inversely related in this scenario.
So, as fluid velocity increases in the tube, the pressure decreases, right?
Yes! Visualizing it helps. Imagine the fluid flow as streams in a river; as they crowd into a narrow section, they speed up while pressure drops. This is crucial in applications like fluid measurement.
To summarize, Venturi tubes leverage pressure changes that occur from velocity changes to measure flow rate effectively.
Bernoulli's Equation Application
Unlock Audio Lesson
Let’s dive deeper into applying Bernoulli’s equation to determine flow rates in Venturi tubes. Who can remind us what we derive from it?
We can find the relationship between pressure and fluid velocity, right?
Yes! The equation expresses the conservation of energy along a streamline. For a horizontal Venturi tube, z1 equals z2. Can anyone express Bernoulli’s equation using pressure and velocity terms?
It would be P1/ρg + V1²/2g = P2/ρg + V2²/2g?
Perfect! Now, what happens if we rearrange to solve for the velocity? How do we calculate the mass flux?
We can substitute the velocity in the continuity equation to express it in terms of pressure differences!
Exactly! This creates a crucial link: the pressure difference drives the fluid flow. Always remember to include the coefficient of discharge for real systems as well.
In summary, by applying Bernoulli's equation correctly, we can derive meaningful results concerning flow rates in Venturi systems.
Energy Gradient & Pressure Gradients
Unlock Audio Lesson
Let’s talk about energy gradients—how do they influence our understanding of flow through Venturi tubes?
Are they related to the mechanical energy losses we also consider?
Exactly! Energy losses occur due to friction and other factors, causing hydraulic gradients to slope downwards, representing energy loss over distance.
So, that means our readings could be less accurate due to these losses?
Yes! When you calculate flow rates, account for these mechanical energy losses. When measuring pressure gradients, ensure you note if they depend on altitude as well. Can anyone think of a way to visualize this?
Maybe graphing pressure against flow rates?
Precisely! Graphical analysis gives a clear understanding of how energy loss translates into pressure losses, helping us predict system behavior more accurately. Let's remember our concepts: gradients indicate loss, while smooth flow indicates efficiency.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
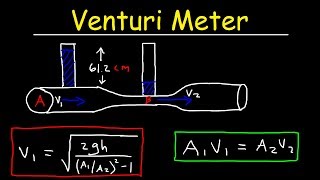
In this section, we discuss Venturi tubes, which are devices that measure fluid flow based on changes in pressure and velocity in a constricted pipe. The principles involve Bernoulli's equation and concepts such as hydraulic gradient lines and mechanical efficiency in fluid systems.
Detailed
Venturi Tube Problem
Venturi tubes are essential instruments in fluid mechanics used to measure fluid flow by exploiting Bernoulli's principle. This section delves into the theoretical basis and practical applications of Venturi tubes, including:
- Basic Concepts of Flow Dynamics: In open channel flow, the hydraulic gradient coincides with the free surface of the liquid, while in pipelines, pressure measurements can be taken using piezometers. Key concepts include pressure head transition at outlets and the effect of mechanical energy losses due to friction.
- Energy Gradient Lines: Mechanical energy losses are crucial, showing that energy gradient lines slope downwards as flow progresses, indicating energy conversion into thermal energy.
- Application of Bernoulli’s Equation: To calculate flow rates and efficiencies in pumping systems, the relationship between mechanical energy inputs and outputs is analyzed, focusing on how pumps increase energy while turbines decrease it.
- Practical Problems Involving Venturi Tubes: We explore how to derive mass flux expressions based on pressure differences measured in the Venturi tube, illustrating calculations and considerations of fluid properties.
- Flow Classification: One-dimensional, incompressible, steady, and frictionless flow principles are emphasized, highlighting how these assumptions simplify the application of Bernoulli's equation.
Overall, the section underscores the significance of Venturi tubes in engineering applications, particularly in determining flow rates based on pressure differentials.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Hydraulic Gradient Lines in Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In open channel flow, the hydraulic gradient lines coincide with the free surface of the liquid because there is no pressure head. The energy gradient lines include the velocity head above the free surface.
Detailed Explanation
In open channel flow, the hydraulic gradient represents the height of the water surface. Unlike closed pipes, where pressure contributes to the hydraulic head, open channels lack pressure heads, so the water surface directly indicates the hydraulic gradient. The energy gradient line accounts for the kinetic energy from the fluid's velocity, which is expressed as the velocity head.
Examples & Analogies
Think of a river; the height of the water surface is like the 'goal line' indicating the hydraulic gradient. When you throw a stone into the river, it creates ripples, which represent the energy gradient from its movement. Here, the water line remains constant, but the motion reflects the energy involved.
Pressure Heads in Pipes vs Open Channels
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When a pipe exits to the atmosphere, the pressure head becomes atmospheric pressure, causing the hydraulic gradient line to coincide with the pipe outlet. Mechanical energy losses due to friction cause both energy gradient and hydraulic gradient lines to slope downward in the direction of flow.
Detailed Explanation
In a pipe system, when the liquid exits, the pressure decreases to atmospheric pressure, represented as a zero pressure head. This transition means that the hydraulic gradient aligns with the outlet of the pipe. Due to mechanical energy losses from friction within the pipe, both the energy and hydraulic gradients experience a downward slope, indicating energy loss as the fluid flows.
Examples & Analogies
Imagine a carnival slide; when kids slide down, they lose some energy due to friction, so they don’t reach the same height at the end compared to where they started. Similarly, in a pipe, the fluid starts with potential energy (pressure), but as it exits, some of that energy is lost to friction, causing the hydraulic gradient to drop.
Pressure Above and Below the Hydraulic Gradient Line
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Pressure in a flow section above the hydraulic gradient line is considered negative, while pressure below the line is positive. This relationship guides how we understand pressure changes in fluid systems.
Detailed Explanation
The hydraulic gradient line serves as a baseline to evaluate pressure. If the pressure at a particular point is above this line, it implies a negative physical pressure, suggesting that this area is void or less than atmospheric pressure. Conversely, if the pressure is below this line, it is deemed positive, indicating that the fluid can exert pressure normally.
Examples & Analogies
Consider a balloon holding air; the atmospheric pressure outside is trying to collapse the balloon (negative pressure situation) if it were damaged. Conversely, inside the balloon, the air pressure is positive because it can expand and push against the outer walls, similar to how fluids behave in a pipe against the hydraulic gradient.
Understanding Pumps and Turbines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Pumps do mechanical work to raise the fluid's pressure, increasing its energy. Turbines operate in the opposite manner, extracting energy from the fluid effectively lowering its pressure.
Detailed Explanation
Pumps are devices that add energy to the fluid, resulting in higher pressure which means the fluid can be moved over long distances. Conversely, turbines convert the kinetic energy of flowing fluid into mechanical energy, leading to a drop in pressure. This is essential in hydroelectric power systems where turbines generate electricity while the pressure drops.
Examples & Analogies
Think about riding a bicycle uphill; pedaling (the pump) is exerting force (supplying energy) to gain altitude (pressure). When descending (using a turbine), the energy you built while climbing is transformed into speed, reducing the effort needed (lowering the pressure).
Bernoulli's Equation and Practical Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Bernoulli's equation can be applied in real-world scenarios to analyze the energy differences between two points in a fluid flow system, often utilizing flow classifications.
Detailed Explanation
Bernoulli's equation is a principle that highlights the conservation of energy in flowing fluids. By applying it to different points in a system, engineers can determine how much mechanical energy is converted between kinetic and potential forms. Understanding flow characteristics like one-dimensional, incompressible, or steady flow enables accurate applications of this equation in practical scenarios such as designing venturi tubes.
Examples & Analogies
Consider a water slide at a theme park; as you go down (higher kinetic energy), the slide's height decreases (lower potential energy). The total energy remains constant, just like what's depicted in Bernoulli's equation. If water flows through a venturi tube, it speeds up, demonstrating how fluid behavior aligns with energy conservation principles.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Venturi Tube: A device measuring flow rates by exploiting the relationship between pressure and fluid velocities in a constricted section.
-
Bernoulli's Equation: A fundamental principle that relates the speed, pressure, and height of a fluid.
-
Mechanical Energy Losses: Energy losses attributed to friction and turbulence, causing pressure drops in fluid systems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
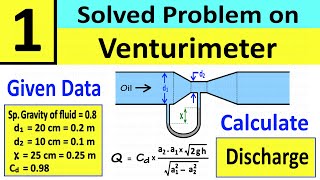
Example 1: Calculate the flow rate through a Venturi tube given a pressure difference and fluid properties.
-
Example 2: Analyze energy losses in a pipeline due to friction when using a Venturi tube for measurement.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a Venturi tube so tight, pressure drops and flow takes flight.
📖 Fascinating Stories
-
Imagine a water hose that narrows at one spot; the water rushes faster, and the pressure drops there, just like in a Venturi tube.
🧠 Other Memory Gems
-
Use 'PVT' - Pressure Velocity Trade: Remember that as pressure goes down, velocity goes up in fluid flow.
🎯 Super Acronyms
VEC
- V: for Velocity
- E: for Energy
- C: for Coefficient of discharge - key concepts in Venturi tube calculations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Venturi Tube
Definition:
A device used for measuring fluid flow, where velocity increases and pressure decreases through a constriction.
-
Term: Bernoulli's Equation
Definition:
An equation that represents the conservation of energy in fluid flows, linking pressure, velocity, and elevation.
-
Term: Mass Flux
Definition:
The rate of mass flow through a given area, often analyzed in relation to pressure differences.
-
Term: Hydraulic Gradient
Definition:
A measure representing the change in hydraulic head per unit distance along a flow path.
-
Term: Coefficient of Discharge (Cd)
Definition:
A dimensionless number that represents the ratio of actual flow to the theoretical flow through a Venturi tube.