Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Hydraulic Gradient Lines
Unlock Audio Lesson
Let’s start by understanding hydraulic gradient lines in open channel flow. Does anyone know how they differ from pipe flow?
I think in open channels, the hydraulic gradient line matches the water surface?
Correct! The hydraulic gradient line in open channel flow coincides with the free liquid surface because there’s no pressure head. In pipe flow, we measure it using a piezometer.
So, how do we measure the energy gradient line?
Great question! In pipe flow, we use a pitot tube to calculate velocity heads which are included in the energy gradient line.
What happens at the exit of a pipe?
At the outlet, the pressure head becomes atmospheric pressure, thus the hydraulic gradient line meets the pipe outlet.
Are there energy losses due to friction?
Yes! Mechanical energy losses due to friction affect the energy gradient line, leading to a downward slope in the direction of flow. Let’s remember the acronym HHAIN for *Hydraulic gradient, Atmospheric pressure, Inlet conditions, and Friction losses*!
So, to summarize, hydraulic gradient lines depend on pressure head, and energy losses occur in both open channels and pipes due to friction.
Pumps and Turbines
Unlock Audio Lesson
Now let's talk about pumps and turbines. What role do you think they play in fluid systems?
Pumps increase the pressure of the fluid, right?
Exactly! Pumps transfer mechanical energy to the fluid by raising its pressure. Turbines, on the other hand, extract energy from the fluid.
How do we measure their efficiency?
Excellent question! We calculate efficiency as the ratio of output energy to input energy. Energy losses including heat and sound should be considered.
What about Bernoulli's equation?
Bernoulli’s equation relates different energy heads in the system, accounting for mechanical energy differences and efficiency. Remember, energy input must equal energy output minus losses!
Could we summarize the roles of pumps and turbines again?
To recap, pumps raise fluid energy, and turbines extract fluid energy. The efficiency measures how well they perform their functions!
Energy Gradient Lines
Unlock Audio Lesson
Let’s examine energy gradient lines. How are they significant in understanding fluid flow?
They show how energy is conserved or lost in the flow?
Exactly! The slope of the energy gradient line represents energy losses due to friction. What do you think could cause these losses?
Friction along the pipe wall, maybe?
Correct! Friction converts some of the mechanical energy into thermal energy, affecting system performance. Remember the acronym LEADS: *Loss of energy And Downward slope due to friction and other losses*.
How do we calculate this loss?
To quantify losses, we can apply Bernoulli’s equation by evaluating energy heads at different pipe sections. This enables us to determine how much energy is converted or lost.
Thanks! Could you summarize what we learned about energy gradient lines?
In summary, energy gradient lines help us visualize how energy losses occur in fluid systems, emphasizing the impact of friction and the need for efficiency!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Mechanical energy losses due to frictional effects in fluid systems lead to downward slopes in energy and hydraulic gradient lines. The role of pumps and turbines in transferring energy and associated losses are also emphasized.
Detailed
Mechanical Energy Losses
In fluid dynamics, mechanical energy losses are significant when analyzing the behavior of fluid flows, especially in pipes and open channels. Understanding hydraulic and energy gradient lines is crucial for predicting how energy is conserved or lost in a system.
Key Points Covered:
- Open Channel vs. Pipe Flow:
- In open channel flow, the hydraulic gradient line coincides with the free surface of the liquid since there is no pressure head. The energy gradient line includes the velocity head above the free surface.
- Pipe flow includes piezometer measurement for hydraulic gradient lines, while pitot tubes measure energy gradient lines.
- Gradient Lines and Energy Losses:
- The hydraulic gradient coincides with atmospheric pressure at pipe exits, which signifies energy loss due to frictional effects. Energy gradient lines typically slope downward in the direction of flow.
- Pressure measured above the hydraulic gradient line indicates negative pressure, while measurements below indicate positive pressure.
- Pumps and Turbines:
- Pumps transfer mechanical energy to fluids by increasing pressures; turbines extract energy by reducing pressures. Their efficient operation is essential in hydraulic systems.
- Efficiency assessments of pumps and turbines help gauge energy transfer effectiveness, accounting for energy losses such as thermal or sound energy.
- Bernoulli's Equation:
- The fundamentals of Bernoulli's equation relate energy terms to the mechanical energy present in flow systems. The implications of pressure head, velocity head, and elevation head are explored at different locations within a pipe system.
This section provides insights into measuring energy losses and optimizing the efficiency of fluid systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Hydraulic and Energy Gradient Lines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
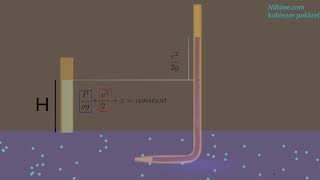
In open channel flow, the hydraulic gradient line coincides with the free surface of the liquid. This is because there is no pressure head. The energy gradient line includes the velocity head above the free surface. In other words, for an open channel, the free surface represents the hydraulic gradient line, and the velocity head V^2/2g added to this gives the energy gradient line. For pipes, however, we can measure the hydraulic gradient lines using a piezometer, and to find the energy gradient line, a pitot tube is needed.
Detailed Explanation
In flows through an open channel, the hydraulic gradient line represents the potential energy of the water level. Since there's no pressure head (pressure measurement in the flow), the surface level of the water defines this line. Additionally, when calculating the energy gradient, we must consider the kinetic energy of the water flow, represented as velocity head (V^2/2g). In pipe flows, we can use tools like a piezometer to directly assess the hydraulic gradient, as there is pressure present. A pitot tube is used to measure the flow's dynamic pressures, enabling the calculation of energy gradients.
Examples & Analogies
Think of a water slide at a theme park. The height of the slide is like the hydraulic gradient – the higher you go, the more potential energy the water has, similar to the water surface in a channel. As the water slides down, it speeds up (increasing velocity head), which is akin to measuring energy at different points along the slide. The pressure felt as the water splashes down at the end can be compared to how we measure energy in pipe systems.
Pressure Changes in Pipe Flows
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When a pipe exits, the pressure head equals atmospheric pressure. Consequently, the hydraulic gradient line coincides with the pipe outlet. When pressure head drops to zero, the hydraulic gradient line aligns with the pipe's exit point. As a result of frictional effects and mechanical energy losses, the energy gradient line slopes downward along the flow direction, indicating a loss of energy through the system.
Detailed Explanation
As fluid exits a pipe, the pressure it exerts equals the pressure of the surrounding atmosphere. This condition signifies that zero pressure head aligns with the hydraulic gradient line at the pipe outlet. Mechanical energy losses occur due to friction within the pipe, which diminishes the energy available for fluid flow, thus creating a downward slope in the energy gradient line. Understanding this helps predict how energy changes along a system of flow, leading to more efficient design and operation in engineering applications.
Examples & Analogies
Imagine a water hose connected to a tap. When you turn on the tap full blast, the water shoots out, but if you pinch the hose just before the end, the pressure builds up inside the hose. Once you release the pinch, the water rushes out freely, but some energy is lost due to the hose's friction, represented by how fast the water flows out compared to starting pressure. The pressure outside the hose is just the air pressure around it.
Energy Losses Impact on Fluid Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mechanical energy losses convert to heat and sound due to friction, resulting in the energy gradient line's downward slope. Additionally, knowing that pressure above the hydraulic gradient line indicates negative pressure and below indicates positive pressure helps analyze pressure variations in flow sections.
Detailed Explanation
In fluid flow systems, energy lost due to mechanical friction not only reduces the energy available for work but also influences the pressures experienced within the system. Friction transforms mechanical energy into heat—this thermal energy isn't harnessed for productive work, and therefore, it contributes to downward trends in both the energy and hydraulic gradient lines. The pressure dynamics surrounding these gradients are critical for understanding how fluid behaves in designs, emphasizing losses and efficient designs.
Examples & Analogies
Think of a long, winding road drive in a car. As you accelerate, you might feel the car's engine working hard. On the other hand, if the road is uphill and rough, some of that energy requires more fuel to maintain speed, resulting in your engine producing more heat than necessary. This excess isn't useful for moving forward and reflects how energy is lost in real-world systems just like friction does in pipes.
Pumps and Turbines in Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Pumps increase fluid pressure by transferring mechanical energy to the fluid, resulting in energy gain. Conversely, turbines extract mechanical energy from moving fluid and drop its pressure. These systems are commonplace in fluid dynamics and require careful analysis of energy input and outputs to determine efficiency.
Detailed Explanation
In mechanical systems, pumps and turbines play crucial roles. A pump works by using mechanical energy to increase the pressure of a fluid, effectively moving it from a lower elevation to a higher one. Turbines do the opposite; they convert the kinetic energy of fluid into mechanical energy used for work, such as generating electricity, by reducing fluid pressure. Understanding their interaction allows engineers to optimize energy use in various applications, leading to enhanced efficiencies across different systems.
Examples & Analogies
Consider a water park where pumps fill up pools. Just as swimmers are lifted to a tall slide and gravity pulls them down, pumps push water up against gravity, increasing energy in the system. Meanwhile, as the water rushes down and spins a turbine (like in a hydroelectric plant), that movement captures energy, taking pressure out but creating useful work, much like generating electricity as a ride goes up and energy is released when sliding down.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic Gradient: The line representing the potential energy based on pressure head.
-
Energy Gradient: Indicates the total mechanical energy, including pressure and velocity heads.
-
Mechanical Energy Loss: Energy losses in a fluid system due to factors like friction.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In an open channel, the hydraulic gradient coincides with the water surface, indicating no pressure head.
-
Upon exiting a pipe, the pressure head becomes atmospheric, illustrating energy losses due to friction.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Energy flows in a pipe, friction slows it down, at the end, atmospheric pressure wears the crown.
📖 Fascinating Stories
-
In a village, there were pipes; the water flowed with joy. But when the friction caught them, it slowed down their ploy. The pumps worked hard, raising the spirits, but the turbines extracted energy, 'til their work was demerits.
🧠 Other Memory Gems
-
Remember P-E-V for understanding the parts of Bernoulli’s: Pressure, Energy, Velocity.
🎯 Super Acronyms
Recall LEADS
- Loss of Energy And Downward slope due to friction and other losses.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Gradient Line
Definition:
The line representing the potential energy of a fluid based on pressure head; it coincides with the free surface in open channels.
-
Term: Energy Gradient Line
Definition:
A line that indicates the total mechanical energy of the fluid, taking into account pressure head, velocity head, and elevation head.
-
Term: Pressure Head
Definition:
The height of a fluid column that a given pressure can support; it contributes to the hydraulic gradient.
-
Term: Piezometer
Definition:
A device used for measuring the pressure of a liquid in a pipe by displaying the height of the fluid column.
-
Term: Pitot Tube
Definition:
An instrument used to measure fluid flow velocity, incorporating works in determining energy gradient lines.
-
Term: Mechanical Energy Losses
Definition:
Loss of energy due to friction and other factors in a fluid flow system, causing differences between input and output energy.
-
Term: Bernoulli’s Equation
Definition:
A principle that describes the conservation of energy in fluid dynamics; it relates the pressure, velocity, and height of a fluid.