Applications of Navier-Stokes and Approximation Methods
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Navier-Stokes Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to explore the Navier-Stokes equations, which are fundamental in fluid mechanics. Can anyone tell me what these equations describe?

They describe the motion of fluid substances.

Exactly! They describe how fluids flow under various forces. Now, can anyone give me a real-world example of where we might apply these equations?

Maybe in predicting weather patterns or understanding ocean currents?

Correct! The applications are vast. Remember, Navier-Stokes equations help us analyze complex fluid behavior. It’s crucial to understand their approximations, such as Euler equations under certain conditions.
Velocity Potential Functions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's talk about velocity potential functions. Can anyone explain what they are in context to fluid flow?

They represent flow fields in irrotational flow.

Exactly! The flow can be described using a scalar potential instead of multiple velocity components. Why is this sometimes easier?

Because it reduces the equations we need to solve, right?

Absolutely! Fewer variables mean simpler calculations. Remember this as it makes working with these equations much more manageable.
Boundary Layer Approximations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's discuss boundary layer approximations. Who can tell me what a boundary layer is?

It's the region close to a solid boundary where the effects of viscosity are important.

Exactly! In the boundary layer, we can approximate the flow behavior. Why do we simplify it like this?

To make the calculations easier and to focus on the most significant effects?

Yes! Approximating these effects allows us to solve complex flow problems more easily. This technique is crucial in engineering applications.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section explores the complexities of fluid flow, delving into the Navier-Stokes equations and their applications in calculating flow in diverse scenarios. It introduces key concepts such as velocity potential functions for irrotational flow, as well as approximation methods to simplify the equations for practical solutions. The connection between fluid dynamics and real-world applications is highlighted.
Detailed
Detailed Summary
In this section, we delve into the fundamental applications of the Navier-Stokes equations, which govern the behavior of fluid flow. The discussion begins with the derivation of simplified equations, including Euler and Bernoulli's equations, from the Navier-Stokes framework. This serves to underscore the importance of these foundational equations in modeling incompressible viscous flows in various contexts.
Key concepts introduced include:
- Velocity Potentials: It is established that in the case of irrotational flows, velocity can be described as the gradient of a scalar potential function, simplifying the analysis to a single function as opposed to multiple velocity components.
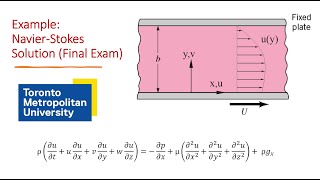
- Boundary Layer Theory: The section discusses boundary layer approximations, particularly how they apply to flows over stationary and moving surfaces. It illustrates how these approximations allow us to analyze velocity distributions in layers close to surfaces where viscous effects are significant.
- Practical Applications: The importance of understanding these equations and methods is emphasized with examples such as flow between plates and the impact of pressure gradients on flow behavior.
The significance of mastering these applications lies in their ability to simplify complex fluid problems into manageable models, paving the way for analytical and numerical solutions that are essential for engineers and scientists in fluid mechanics.
Youtube Videos

![[Fluid Dynamics: Application] A simple application of Navier-Stokes equation](https://img.youtube.com/vi/6Hze7GwY3Ng/mqdefault.jpg)
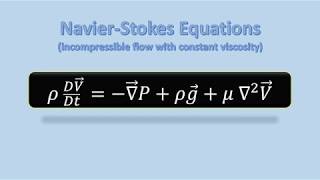





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Velocity Potentials
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
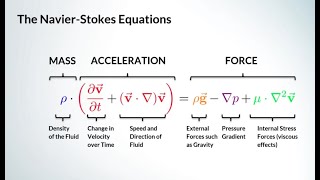
So basically let us start with Navier-Stokes equations which is long back about 200 years back. So the equations what we derive in last two classes we will go more detail about that. Before going that let me I just write down the basics equations is the Euler equations okay.
Detailed Explanation
This section introduces the Navier-Stokes equations, which have their roots in fluid dynamics dating back over 200 years. The instructor aims to recap the Euler equations, which are a simplified version of the Navier-Stokes equations applicable to incompressible and non-viscous flows. Understanding these basic equations is crucial for applying more complex fluid dynamics concepts.
Examples & Analogies
Think of the Navier-Stokes equations as the 'rules of the road' for fluid flow, similar to how traffic laws guide vehicles. Just as understanding basic traffic rules helps drivers navigate better, grasping the fundamentals of the Navier-Stokes equations allows scientists and engineers to predict how fluids will behave in various situations.
Understanding Euler Equations and Flow Dynamics
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you look it when I talk about Euler equations you can understand it. It is for incompressibles and non-viscous or fixed or less flow. So this is the reasons we can apply it that means if you consider flow past a tall building okay a high rise buildings okay flow past tall building.
Detailed Explanation
Euler equations describe the motion of flows that are considered incompressible and non-viscous. This chunk illustrates their application using the example of airflow around a tall building. The discussion emphasizes how the equations work well outside the region where viscous effects and turbulence occur, highlighting their limitations near structures.
Examples & Analogies
Imagine a car driving smoothly down a highway (Euler flow) versus driving through an obstacle course where the terrain is bumpy and has barriers (Navier-Stokes flow). The car's speed and direction can be predicted easily on the highway, much like the Euler equations predict fluid behavior in ideal conditions. However, once obstacles are introduced, like buildings or rough terrain, the predictions become complex, requiring more advanced equations.
Introduction to Velocity Potential Functions
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The basic idea comes that can you write these equations with a single scalar value okay that is the simple idea comes is that instead of looking at 3 scalar velocity component why we cannot write it with a simple a scalar functions that is what is the velocity potential function.
Detailed Explanation
This segment introduces the concept of velocity potential functions, which simplify the complex relationships in fluid dynamics. It proposes that instead of working with three velocity components (u, v, w), a single scalar function could adequately represent the system's dynamics if specific conditions (like irrotational flow) are met, facilitating easier computations.
Examples & Analogies
Think of velocity potential functions as using a simple map to navigate a complex city. Instead of dealing with multiple roads (velocities), a single map (the potential function) provides an overarching view that makes it easier to find your way, provided you are only looking for routes that don’t have obstacles (irrotational flow).
Conditions for Using Velocity Potential Functions
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Thus if I define it the velocity is a gradient of phi, phi is a velocity potential function at which condition thus this is what justified it was. If you look at the very basic components if I velocity potentials.
Detailed Explanation
In this part, the conditions for using velocity potential functions are discussed. It emphasizes that these functions can be applied in irrotational flows, meaning the fluid does not have any rotation. Such conditions simplify the calculations while predicting fluid behavior accurately in certain scenarios.
Examples & Analogies
Imagine a smooth, calm pond where a rock is thrown in—it creates ripples but doesn’t swirl. Here, the water behaves in an irrotational manner, much like the ideal conditions for using velocity potential functions. On the other hand, a rapid whirlpool represents a rotational flow where these functions cannot be applied.
Implications of Irrotational Flow
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So the conditions what we have the flow should be the irrotational flow field or the regions where the rotational activities merely or negligible components okay.
Detailed Explanation
This section stresses the importance of irrotational flows for applying the derived potential functions. It reinforces that fluid flows can only be simplified to scalar potential functions under specific conditions, avoiding scenarios where rotational activities would complicate the equations.
Examples & Analogies
Think of a smooth river flowing gently; you can easily measure its speed and direction because it lacks deep eddies and whirlpools (irrotational). If the river were turbulent with whirlpools, measuring its flow would become significantly harder, similar to how rotational flows challenge fluid mechanics predictions.
Applications of Navier-Stokes Equations in Practical Scenarios
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now if you look at that at which condition does it satisfy.
Detailed Explanation
The teaching connects the theoretical aspects learned earlier to practical applications of the Navier-Stokes equations. These equations are vital in modeling fluid dynamics across various fields, allowing for accurate predictions in engineering, meteorology, oceanography, and even medicine.
Examples & Analogies
Consider a scenario where engineers need to design a dam. The proper deployment of Navier-Stokes equations helps predict how water will flow both over and around the dam, ensuring it can withstand potential floods without breaking—just as accurately predicting weather patterns relies on similar fluid dynamics.
Key Concepts
-
Simplification of Navier-Stokes: The Navier-Stokes equations can be simplified for specific flow types.
-
Velocity Potentials: Functions that reduce multiple velocity components to a single scalar function in irrotational flow.
-
Boundary Layers: Layers near surface boundaries where viscosity effects must be considered.
Examples & Applications
Flow past an object: The behavior of fluid flowing around a tall building can be modeled using Navier-Stokes equations to understand turbulence and separation.
Simple shear flow: The velocity distribution between stationary and moving plates illustrates the use of approximation methods using Navier-Stokes.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Navier-Stokes equations, oh so grand, they describe the flow across the land.
Stories
Imagine a river flowing smoothly around rocks; that's like fluid moving described by Navier-Stokes.
Memory Tools
Use the acronym BLISS for boundary layers: 'Boundary, Layer, Impacts, Shear, Simplify'.
Acronyms
VAP
Velocity
Approximation
Potential – a reminder of simplifying complex flows.
Flash Cards
Glossary
- NavierStokes Equations
A set of equations describing the motion of fluid substances, accounting for viscous and pressure forces.
- Velocity Potential Functions
Functions representing flow fields in irrotational flow, expressed as the gradient of a scalar potential.
- Boundary Layer
The region of fluid flow near a solid boundary where viscous effects are significant.
- Bernoulli's Equation
An energy conservation equation for incompressible flow, deriving from the principles of fluid dynamics.
- Euler Equations
Equations governing inviscid flow derived from the Navier-Stokes equations under specific assumptions.
Reference links
Supplementary resources to enhance your learning experience.
