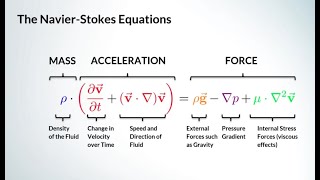
Navier-Stokes Equations Recap
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Navier-Stokes Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning everyone! Today, we are revisiting the Navier-Stokes equations. Does anyone remember what kind of problems these equations help us solve in fluid mechanics?

They help us analyze how fluids move, right?

Exactly! The Navier-Stokes equations describe the behavior of viscous fluid substances. Who can tell me what the key variables in these equations are?

Pressure, velocity, and viscosity!

Correct! And remember, we can represent the velocity in terms of velocity potential under certain conditions. Can anyone explain the conditions needed?

The flow must be irrotational!

Right again! For irrotational flows, we can simplify our equations significantly by using scalar potential functions. Great job, everyone!
Applications of Navier-Stokes Equations in Incompressible Viscous Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

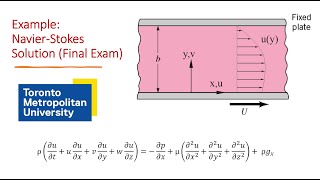
Let's discuss some applications. For example, how can we use these equations to understand flow between two plates?

We can see how velocity changes as one plate moves and how the pressure gradients influence that flow!

Exactly! If one plate is fixed and the other moves, the flow profile we get is crucial. Can anyone explain how we would simplify our calculations in this scenario?

We could ignore gravity since the flow is horizontal!

Good point! Ignoring gravity and assuming a steady state flow simplifies our Navier-Stokes equations tremendously. Remember, approximations play a key role!
Understanding Velocity Potentials
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s delve into the velocity potentials concept. What role do they play in analyzing fluid flow?

They help reduce multiple variables into a single function, making it easier to solve problems!

Yes! This approach reduces complexity. Can anyone summarize the key conditions for applying velocity potentials?

The flow has to be incompressible and irrotational!

Exactly. These conditions ensure that we can use the gradient of the velocity potential to describe the velocity field. Why is that important?

It helps us visualize the flow field better!

Absolutely! Understanding these concepts is critical for modeling real fluid systems.
Visualizing Fluid Flow with Streamlines
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s visualize our fluid flow. Who can tell me how streamlines are related to the velocity potential functions?

Streamlines represent the paths along which fluid particles move, and they are orthogonal to equipotential lines!

Very well stated! The orthogonality is key here. Remember the relationship between the potential functions and the velocity fields. Can anyone provide an example of where this might be seen in real life?

Flow around buildings or objects in the wind!

Exactly! Understanding this relationship helps in many engineering applications.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section revisits the foundational aspects of the Navier-Stokes equations, demonstrating their role in deriving various other important equations in fluid mechanics, such as the Euler and Bernoulli equations. It explores applications, illustrating how to analyze incompressible viscous flow through different setups.
Detailed
Detailed Summary
In this section, we delve into the Navier-Stokes equations, which form the fundamental basis for understanding fluid dynamics. We begin by recapping previous discussions about how the Navier-Stokes equations relate to other essential equations like Euler's equations and Bernoulli's equations. The instructor emphasizes the importance of velocity potentials in analyzing fluid flow, particularly under conditions of incompressibility and viscosity.
Key focuses include:
- Velocity Potentials: Introduced as a means to simplify the analysis of fluid flows, representing velocity as a scalar potential that can reduce complexity in calculations. The section elaborates on the conditions that must be met for velocity potential functions to apply— specifically, the need for an irrotational flow.
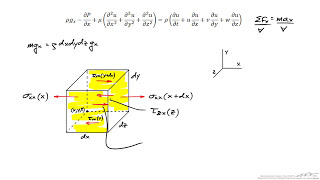
- Incompressible Viscous Flow: Discussions cover various scenarios of flow patterns: flow between fixed and moving plates due to pressure gradients and incompressible viscous flow within cylinders. The essence of deriving simple solutions using the Navier-Stokes equations is thoroughly explored, emphasizing how assumptions can streamline analysis in practical situations.
- Applications and Visualizations: The use of graphical representations of velocity fields through streamlines and potential functions underscores the practical applications of these equations. The narratives foster an understanding of the dynamics of flow in real-world situations, encouraging critical thinking as students are prompted to engage with the material actively.
This section serves as a foundation for further studies and applications of fluid mechanics, establishing a crucial link between theory and real-world dynamics.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Navier-Stokes Equations
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So basically let us start with Navier-Stokes equations which is long back about 200 years back. So the equations what we derive in last two classes we will go more detail about that.
Detailed Explanation
The Navier-Stokes equations are fundamental equations in fluid mechanics that describe the motion of fluid substances. They were developed over 200 years ago and have been foundational in understanding how fluids behave in various situations. In this section, we will build upon what was previously covered regarding these equations.
Examples & Analogies
Think of the Navier-Stokes equations as the 'rules of the road' for fluids. Just as traffic rules dictate how cars move, these equations dictate how fluid particles move and interact with each other and their surroundings.
Euler Equations and Their Application
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Before going that let me I just write down the basics equations is the Euler equations okay. ... But newer to structures as the vorticity is there, the turbulence behaviors are there as well as it has the flow separations that is what is not valid for this external flow.
Detailed Explanation
The Euler equations are derived from the Navier-Stokes equations under the assumption of inviscid flow (no viscous forces). These equations apply primarily to incompressible, non-viscous flows. In practical scenarios, like wind passing tall buildings, the flow can be approximated with Euler equations, but near the structures, where turbulence and vortices occur, these equations do not hold well.
Examples & Analogies
Imagine a river flowing past a rock. The water flows smoothly without interaction (similar to Euler's assumptions) until it encounters the rock, creating turbulence and whirlpools. This reflects how Euler equations are valid where the flow is smooth and laminar but break down in turbulent areas.
Velocity Potential Functions
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The basic idea comes that can you write these equations with a single scalar value okay that is the simple idea comes is that instead of looking at 3 scalar velocity component why we cannot write it with a simple a scalar functions that is what is the velocity potential function.
Detailed Explanation
The concept of velocity potential functions simplifies the analysis of fluid flow by representing the flow velocity as the gradient of a scalar function, known as the velocity potential. Instead of dealing with three separate components of velocity, which can complicate calculations, a single scalar function can provide the same information in a more manageable way. This approach is particularly useful in irrotational flow conditions.
Examples & Analogies
Consider measuring temperature across a field. Instead of checking the temperature at every point (like measuring each velocity component), you could describe the entire field with a single temperature map. The velocity potential function acts similarly, capturing the essence of the flow in a simplified manner.
Conditions for Irrotational Flow
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Thus if I define it the velocity is a gradient of phi, phi is a velocity potential function... That means if I again coming back to the same flow first a tall building if I draw the two streamlines.
Detailed Explanation
The irrotational flow condition is key to applying velocity potential functions. It states that in regions where the fluid behaves without rotation, the velocity can be represented as a gradient of a potential function. When taking flow measurements around structures, the flow may become rotational; thus, the conditions of irrotational flow are essential for accurate calculations using potential functions.
Examples & Analogies
Imagine a calm lake surface reflecting the sky. This reflects an irrotational condition—the water flows smoothly without any disturbances. However, if a stone is thrown into the lake, waves and vortices form, creating an 'irrotational' disruption to that calm state.
Streamlines and Velocity Potential Lines
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We need to draw the streamlines and the potential lines to show it that because just you interpreted the gradient of the velocity potential functions indicates as the velocity field that is very interesting part of here.
Detailed Explanation
Streamlines and velocity potential lines visualize fluid flow, with streamlines representing the path of fluid motion and velocity potential lines illustrating the potential function. Both types of lines are crucial for understanding flow patterns, and their orthogonality signifies that they intersect at right angles, which is essential in two-dimensional irrotational flow.
Examples & Analogies
Think of a road map with streets (streamlines) and altitude lines (potential lines). The streets show where cars can go while the altitude lines indicate heights. In this analogy, cars follow streets smoothly, just as fluid particles follow streamlines, while altitude lines help visualize energy transitions in the flow.
Rotationality in Fluid Flow
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now if you look at very interesting part which I can relate it with very basic equations what you know it is the Newton's first law of motions is you know it if you look at that Newton's laws first law of motions okay you know with the three laws okay.
Detailed Explanation
This section correlates the concept of rotationality in fluid dynamics with Newton's first law of motion. It explains that just as a body remains at rest or moves uniformly in a straight line unless acted upon by an external force, an irrotational flow remains unchanged without external influences. When disturbances occur, like obstacles in the flow path, they create rotation within the fluid.
Examples & Analogies
Imagine riding a bicycle on a straight flat road. If you keep pedaling evenly without any obstacles, you move smoothly (irrotationality). If you suddenly hit a curb (external force), the bike's direction and flow (just like fluid behavior) change, causing rotational behavior.
Key Concepts
-
Navier-Stokes Equations: Fundamental equations for fluid flow.
-
Velocity Potentials: Scalar function representing velocity in irrotational flows.
-
Incompressible vs. Compressible Flow: Difference based on density.
-
Irrotational Flow: A flow with no internal rotation, allowing simplified analysis.
-
Viscosity: Determines the resistance of fluids to flow.
Examples & Applications
Flow between a fixed plate and a moving plate illustrating shear stress.
Viscous flow in a cylinder demonstrating pressure gradients.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In flow so fine, with viscosity's bind, Navier-Stokes, the answer you will find!
Stories
Once in a fluid world, a wise old equation named Navier-Stokes helped engineers understand how structures influence the flows around them, letting them design better buildings and vehicles.
Memory Tools
V.I.R: Viscosity, Irrotationality, and Relativity. Remember the three pillars of fluid mechanics when applying Navier-Stokes.
Acronyms
NAV
Navier
Analysis
Velocity.
Flash Cards
Glossary
- NavierStokes Equations
A set of equations that describe the flow of fluids, accounting for viscosity.
- Velocity Potential
A scalar function from which the velocity field can be derived in irrotational flows.
- Incompressible Flow
Flow where the fluid density is constant.
- Irrotational Flow
Flow in which the fluid has no rotation about any point.
- Viscosity
A measure of a fluid's resistance to deformation or flow.
Reference links
Supplementary resources to enhance your learning experience.
