Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Velocity Potentials
Unlock Audio Lesson
Good morning everyone! Today, we're diving deep into the concept of velocity potentials. Can anyone tell me what a velocity potential is?
Is it a function that helps us express the velocity of a fluid?
Exactly! Velocity potentials allow us to express the velocity field of a fluid in terms of a scalar function. This makes our calculations much simpler. Remember, if we have a potential function, we can derive the velocity components from it!
How do we actually derive those components?
"Good question! The velocity components u, v, and w can be expressed as:
Irrotational Flow Criteria
Unlock Audio Lesson
Now, let's discuss irrotational flow. What does it mean for a flow to be irrotational?
It means the flow has no rotation or vorticity, right?
Correct! For flow to be considered irrotational, we must ensure certain conditions are satisfied. Can anyone recall those conditions?
One condition is that the velocity potential function should have continuous derivatives.
Exactly! And it leads us to apply these concepts in practical scenarios such as flow past buildings. Remember, if the flow can be considered irrotational, it allows us to use the velocity potential function for analysis!
Application of Bernoulli's Equation
Unlock Audio Lesson
Next, we will connect these concepts with Bernoulli's equation. Can anyone tell me what Bernoulli's equation states?
It relates the pressure, velocity, and height in a flowing fluid.
Exactly! Bernoulli's equation is critical in understanding fluid behavior in different scenarios. For instance, can anyone tell me how it helps when applied to internal or external flows?
It helps us analyze the energy balance within a flowing fluid, making it possible to predict how changes in velocity or pressure can affect the fluid's motion.
Well put! This understanding allows us to visualize flow patterns and evaluate real-world fluid dynamics, like flow around buildings and in pipes.
Evaluating Flow Between Plates
Unlock Audio Lesson
Let's apply what we've learned to evaluate flow between two plates. What happens when one plate is stationary, and the other moves?
The velocity gradient will change, causing shear stress in the fluid!
Correct! We can analyze that using our velocity potential function. Does anyone remember how we derive velocity profiles in such scenarios?
By solving the Navier-Stokes equations under certain assumptions, right?
Absolutely! After finding the velocity gradient, we can determine the velocity field, shear stress, and pressure gradient across the fluid. Can anyone summarize why understanding these relationships is crucial?
It helps engineers design systems more effectively by predicting how fluids will behave under different conditions!
Excellent! You've all grasped key concepts that are foundational in fluid mechanics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section focuses on the derivation of concepts related to velocity potentials and their application to analyze fluid flow through various scenarios, such as flow past buildings and viscous flow between plates. It highlights the conditions needed for irrotational flow and the simplifications that lead to the use of Bernoulli's equations.
Detailed
Velocity Potentials and Pressure Gradients
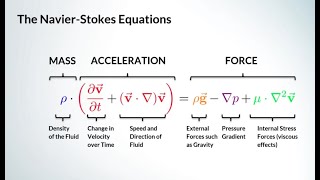
In fluid mechanics, the relationship between velocity potentials and pressure gradients is critical for understanding the behavior of fluid flow. This section discusses how the Navier-Stokes and Euler equations form the foundation for deriving the Bernoulli equations, which are crucial for analyzing fluid dynamics.
Key Concepts:
- Velocity Potentials: The velocity field of a fluid can be represented as a gradient of a scalar potential function. This results in a simplified analysis, where:
- Velocity components are represented as:
$$
u = \frac{\partial \phi}{\partial x}, \quad v = \frac{\partial \phi}{\partial y}, \quad w = \frac{\partial \phi}{\partial z}
$$
- This simplification applies under the condition of irrotational flow, where vorticity approaches zero.
- Irrotational Flow: For fluid flow to be treated as irrotational, certain conditions must be satisfied. The flow must not exhibit rotational behavior, which allows for the use of velocity potentials for solving problems more straightforwardly.
- Bernoulli's Equation: This fundamental equation connects the velocity field and pressure gradient in fluid mechanics, allowing for calculations of fluid behavior under certain conditions like inviscid flow.
- Applications: The section includes practical scenarios, such as flow past buildings and simple flows between fixed and moving plates, leading to performance evaluations of various fluid systems.
Overall, this section emphasizes the profound impact of understanding velocity potentials and pressure gradients in solving complex fluid mechanics problems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Velocity Potentials
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So basically let us start with Navier-Stokes equations which is long back about 200 years back. So the equations what we derive in last two classes we will go more detail about that. Before going that let me I just write down the basics equations - the Euler equations.
Detailed Explanation
This chunk introduces the concept of velocity potentials in fluid mechanics and provides historical context by mentioning the Navier-Stokes equations and Euler equations. The Navier-Stokes equations are fundamental in fluid mechanics and describe how fluids behave. The Euler equations, derived from the Navier-Stokes equations, are applicable to incompressible and non-viscous flows.
Examples & Analogies
Think of fluids like cars on a highway. Just as cars have different speeds and routes, fluids flow at varying rates depending on forces acting on them (like pressure or gravity). The equations help us predict the flow behavior much like traffic laws help manage vehicle movements.
Velocity Potential and Flow Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The basic idea comes that can you write these equations with a single scalar value okay that is the simple idea comes is that instead of looking at 3 scalar velocity components why we cannot write it with a simple scalar functions that is what is the velocity potential function.
Detailed Explanation
In this section, the text explains how the complex flow equations can be simplified by introducing a single scalar function known as the velocity potential function. This function reduces the number of variables needed to describe the flow from three velocity components (u, v, w) to one potential function, thus simplifying calculations.
Examples & Analogies
Imagine you have a complex recipe with many ingredients (u, v, w). By creating a 'master ingredient' that represents the essence of your dish (the velocity potential function), you simplify the cooking process and focus on just one key item, making it easier to follow and manage.
Conditions for Using Velocity Potential Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus if I define it the velocity is a gradient of phi, phi is a velocity potential function at which condition thus this is what justified it,... This means the conditions should be satisfied to have the application of velocity potential functions.
Detailed Explanation
In this part, the text discusses the specific conditions under which velocity potential functions can be successfully applied. It mentions that these functions are valid primarily in irrotational flow situations, where the flow doesn't exhibit rotational motion. If the flow has rotational behaviors, such as the presence of vortices, then these potential functions wouldn't apply.
Examples & Analogies
Think of throwing a ball in a straight line versus spinning it. The ball’s straight trajectory is like irrotational flow, where predictions are simple. If you spin the ball and it curves, like rotational flow, predicting its path becomes much more complicated—just as it would be in fluid dynamics.
Streamlines and Potential Lines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look at that at which condition does it satisfy... the velocity potential functions which we define it v is equal to grade phi.
Detailed Explanation
This chunk discusses the relationship between streamlines, potential lines, and their orthogonality. It states that the velocity potential function can be used to find streamlines since the vector field corresponding to the velocity potential is represented as a gradient. Streamlines represent the paths that fluid elements follow, while potential lines show potential differences in the flow field.
Examples & Analogies
Imagine a river with curved banks (streamlines) where you can only travel straight (potential lines). The way the river flows represents how the water moves smoothly along the bank but must adjust when faced with obstacles, much like how potential functions direct fluid movement.
Understanding Irrotational Flow and its Implications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
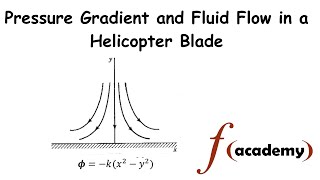
If you look at again for the same tall buildings and draw two streamlines okay the psi equal to 1 psi equal to 2... the conditions you can understand it because stream functions need conditions that flow should be two-dimensional.
Detailed Explanation
Here, the discussion focuses on how streamlines and potential functions relate to each other in the context of fluid flow around structures, with particular emphasis on irrotational flow. It elaborates on the requirement for the flow to be two-dimensional to apply these concepts effectively, illustrating the necessary conditions for drawing meaningful results from potential functions and streamlines.
Examples & Analogies
Consider a flat cake where you can easily cut it into layers (2D flow). If you were to try this on a multi-layered, uneven cake (3D flow), your cuts would become unpredictable. The same idea applies in fluid mechanics: in a straightforward situation (2D), it's easier to predict how the fluid flows.
Pressure Gradients and Flow Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
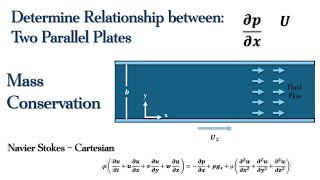
Now coming back to doing some simple approximations using Navier-Stokes equations to get simple solutions between a fixed and moving plate viscous flow if you have... what should be the shear stress distributions that is what we are looking at for viscous flow.
Detailed Explanation
This part describes how to apply the Navier-Stokes equations to analyze the shear stress distributions in a viscous flow between two plates, one fixed and the other moving. It emphasizes the importance of simplifying assumptions in order to derive meaningful results from the equations and how these approximations lead to the understanding of flow behavior under various conditions.
Examples & Analogies
Think about spreading butter on bread. The fixed slice of bread represents the stationary plate, and your knife is like the moving plate. The way the butter (fluid) flows or resists movement (shear stress) depends on how hard you push the knife (forces acting on the fluid), and this relationship can be understood through mathematical equations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Velocity Potentials: The velocity field of a fluid can be represented as a gradient of a scalar potential function. This results in a simplified analysis, where:
-
Velocity components are represented as:
-
$$
-
u = \frac{\partial \phi}{\partial x}, \quad v = \frac{\partial \phi}{\partial y}, \quad w = \frac{\partial \phi}{\partial z}
-
$$
-
This simplification applies under the condition of irrotational flow, where vorticity approaches zero.
-
Irrotational Flow: For fluid flow to be treated as irrotational, certain conditions must be satisfied. The flow must not exhibit rotational behavior, which allows for the use of velocity potentials for solving problems more straightforwardly.
-
Bernoulli's Equation: This fundamental equation connects the velocity field and pressure gradient in fluid mechanics, allowing for calculations of fluid behavior under certain conditions like inviscid flow.
-
Applications: The section includes practical scenarios, such as flow past buildings and simple flows between fixed and moving plates, leading to performance evaluations of various fluid systems.
-
Overall, this section emphasizes the profound impact of understanding velocity potentials and pressure gradients in solving complex fluid mechanics problems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In the case of flow past a tall building, we can analyze external flow using Bernoulli's equation due to the validity of Euler's equations in irrotational flow regions.
-
When studying the flow between two plates, the analysis of velocity gradients provides insights into shear stresses and overall fluid behavior.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluid's flow, potential's the key,
Find the velocity, just look and see!
📖 Fascinating Stories
-
Imagine a flowing river, smooth and clear, with no twists or turns, a perfect sphere; that's irrotational flow, gentle and light, where the velocity potential is always in sight.
🧠 Other Memory Gems
-
To remember Bernoulli, think: 'Pressure High, Velocity Low', it's how fluids ebb and flow.
🎯 Super Acronyms
BVP
- Bernoulli - Velocity - Pressure
- remember the trio for fluid measure!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Velocity Potential
Definition:
A scalar function whose gradient gives the velocity vector of the fluid, simplifying analysis in irrotational flow cases.
-
Term: Irrotational Flow
Definition:
Flow characterized by the absence of vorticity, allowing the use of velocity potential functions.
-
Term: Bernoulli's Equation
Definition:
An equation that describes the conservation of energy in a flowing fluid, relating pressure, velocity, and height.
-
Term: NavierStokes Equations
Definition:
A set of equations governing the motion of fluid substances that account for viscosity.
-
Term: Pressure Gradient
Definition:
The rate of change of pressure in a fluid with respect to distance, which influences fluid flow.