Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Euler Equations
Unlock Audio Lesson
Good morning, everyone. Today, we’ll explore the Euler equations, vital in fluid dynamics. These equations come from the Navier-Stokes equations, simplifying our understanding of fluid behavior.
Can you explain why we need to derive the Euler equations?
Great question! The Euler equations help us analyze incompressible, non-viscous flows, essential for many engineering applications.
What kind of flows can we use these equations for?
We can apply them for various scenarios, such as flow around tall buildings or between two parallel plates. Remember, these equations are most valid away from the boundaries.
Velocity Potential Functions
Unlock Audio Lesson
Let’s now talk about velocity potential functions. These functions help us express fluid velocity in a more simplified manner.
How do they work in relation to the Euler equations?
Good query! When the flow is irrotational—meaning there’s no rotation in the fluid—these potentials can be expressed as a gradient, linking it to velocity.
So we can replace multiple velocity components with a single scalar value?
Exactly! By using a single scalar function, we streamline the analysis, making it easier to solve complex flow problems.
Irrotational Flow and Conditions for Use
Unlock Audio Lesson
Let’s emphasize irrotational flow now. The velocity potential functions can only be used under specific conditions—namely, when the flow is indeed irrotational.
How do we know when to use these functions?
You should assess if vorticity exists in your flow. If it does, it cannot be considered irrotational, and you’ll need other methodologies.
What happens to flow around structures like buildings?
Great example! Near the structures, turbulence occurs, causing vorticity. Thus, the Euler equations can only apply outside those viscous regions.
Applications and Limitations of Euler Equations
Unlock Audio Lesson
Now, let’s recap the applications of Euler equations. They are perfect for analyzing flows where viscosity is negligible, like air flowing over a tall building.
Are there cases where we should not use them?
Yes! When we encounter viscous flows or turbulent behaviors, the Navier-Stokes equations are far more appropriate.
Can you give us a real example of incorrect usage?
Sure! If we were to apply the Euler equations in pipe flow situations where fluids experience significant viscous force, it would yield incorrect results.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the derivation and application of the Euler equations from the Navier-Stokes equations, illustrating their validity for specific flow scenarios, particularly for incompressible and non-viscous flow conditions. The concept of velocity potential functions is introduced, enhancing the understanding of flow fields.
Detailed
Detailed Summary of Euler Equations Overview
In the context of fluid mechanics, the Euler equations serve as a fundamental component in analyzing fluid flows, specifically incompressible and non-viscous scenarios. Derived from the Navier-Stokes equations, the Euler equations are vital for understanding the motion of fluids in various conditions, excluding the boundaries that exhibit significant viscous forces.
In this section, Professor Dutta discusses the significance of velocity potentials as a concise way to represent fluid flow, especially highlighting their value in simplifying the complexities associated with multiple velocity components. The utility of these equations is exemplified through scenarios such as flow past tall buildings and between plates, emphasizing how Euler's equations can accurately describe flow behavior in regions devoid of turbulent effects.
Moreover, the section delves into the characteristics of irrotational flows, making it clear that velocity potentials can only be employed under specific conditions. The capped nature of how flow fields behave when subjected to rotational activity is elaborated upon, augmenting students' understanding of the core principles governing fluid dynamics.
Youtube Videos
![Euler's Equation Concept [Fluid Mechanics]](https://img.youtube.com/vi/-wI3PpWc7L8/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Euler Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look it when I talk about Euler equations you can understand it. It is for incompressibles and non-viscous or fixed or less flow.
Detailed Explanation
Euler equations apply to fluid flows that are incompressible (meaning their density remains constant) and non-viscous (not significantly affected by viscosity). This means that we can use these equations to describe fluid behavior in situations where friction can be ignored, such as in idealized flows.
Examples & Analogies
Think of water flowing smoothly through a wide, straight pipe. As long as there are no obstructions and no friction, the flow behaves as described by Euler equations. However, if you were to narrow the pipe or introduce sharp bends, the flow would become affected by viscosity, and other equations like Navier-Stokes would be needed.
Application of Euler Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For example, if you consider flow past a tall building, Euler equations can describe the flow outside structures but not close to them where turbulence occurs.
Detailed Explanation
When analyzing the airflow around a tall building, the Euler equations help us understand the streamlines of the flow that is far from the building's surface. However, near the structure, the flow can become turbulent and rotational, meaning the Euler equations no longer apply accurately in that region.
Examples & Analogies
Imagine standing next to a tall building on a windy day. As you move away from the building, the wind feels steady and calm. But right next to the building, the wind is swirling unpredictably. This changing behavior illustrates where Euler equations can and cannot be used.
The Form of Euler Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
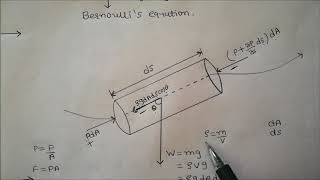
The basic form of the equations is represented as rho * T * (dV/dt) = rho * g - grad(p).
Detailed Explanation
In the Euler equations, 'rho' represents the fluid density, 'T' represents the volume of fluid, 'dV/dt' is the acceleration of the fluid, 'g' is the gravitational field, and 'grad(p)' signifies the pressure gradient in the fluid. This equation essentially balances the forces acting on a fluid element.
Examples & Analogies
Consider a soccer ball being kicked. The ball accelerates due to the force of your kick (analogous to 'rho * g') and experiences resistance from the air (analogous to the pressure gradient). The Euler equation helps describe this motion by linking these forces directly.
UnknownVariables in Euler Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In Euler equations we still have four unknowns: u, v, w, and p (the pressures).
Detailed Explanation
The variables 'u', 'v', and 'w' represent the three velocity components in the fluid, while 'p' is the pressure. To close the system of equations and find a solution, we need additional equations or relationships that relate these variables.
Examples & Analogies
Imagine being a detective with four mysterious clues (the velocities and pressure) but only one statement from a witness (the Euler equations) to work with. You would need more information, like more statements or evidence (additional equations), to solve the mystery.
Velocity Potential Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Instead of looking at three scalar velocity components, we can represent these with a single scalar function called the velocity potential function.
Detailed Explanation
By using a single scalar function known as the velocity potential instead of three separate velocity components, we simplify the problem. The velocity components can be derived from the gradient of this potential function. This is especially useful in irrotational flows, where the velocity can be expressed more easily and significantly reduces complexity.
Examples & Analogies
Think of using a map where you only track your location through one point rather than multiple coordinates. This simplifies navigation and focus, just like how the velocity potential function simplifies fluid flow analysis.
Conditions for Velocity Potential
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The condition for using velocity potential functions is that the flow must be irrotational.
Detailed Explanation
For velocity potential functions to be applicable, the flow must not exhibit any vorticity or rotation, which defines an irrotational flow. This is a crucial condition, as any rotational motion would render the potential function invalid.
Examples & Analogies
Imagine a calm pond where water flows smoothly without any ripples (irrotational). If you throw a stone, it creates circular ripples, which introduces rotational motion and invalidates the use of the potential function to describe the water's movement.
Orthogonality of Streamlines and Potential Lines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The flow net consists of streamlines and equipotential lines that intersect orthogonally.
Detailed Explanation
In fluid dynamics, streamlines represent the paths of fluid particles, while equipotential lines represent points of equal potential energy. The principle of orthogonality states that these lines intersect at right angles when the flow field is irrotational, denoting a fundamental relationship between them.
Examples & Analogies
Think of a street map where the roads (streamlines) intersect with park boundaries (equipotential lines). At every intersection, you can find a right angle, representing how flow paths and potential energy fields relate to one another.
Conclusion on Euler Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Euler equations provide a fundamental framework for analyzing incompressible, non-viscous flow, but are limited in turbulent conditions.
Detailed Explanation
The Euler equations are vital for understanding fluid behavior in ideal conditions (low viscosity and incompressible), but as environmental and situational complexities arise (like turbulence or viscosity), their limitations become apparent, and more complex equations like Navier-Stokes need to be employed.
Examples & Analogies
It's like using a simple recipe for baking a cake (Euler equations), which works when everything goes as planned, but fails when you want to decorate that cake intricately (introducing turbulence and complexities). For that, you need a more detailed recipe (Navier-Stokes equations) to handle those additional layers.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Euler Equations: Essential equations for analyzing flow in incompressible, non-viscous fluids.
-
Velocity Potentials: Simplifies multiple velocity components into a single scalar function.
-
Irrotational Flow: Critical condition for utilizing velocity potentials.
-
Flow Separation: Occurs near solid boundaries where the flow does not follow the surface.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Flow over a tall building can be analyzed using Euler equations away from the structure.
-
Velocity potentials can be used to simplify flow calculations in irrotational scenarios.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Euler means less fuss, with flows that don't combust.
📖 Fascinating Stories
-
Once upon a time, in a fluid land, a stream flew free without a twist or bend, its path was marked by potentials grand, a tale of Euler was in high demand.
🧠 Other Memory Gems
-
Remember EIV for Euler: E for Equations, I for Incompressible, V for Velocity potentials.
🎯 Super Acronyms
FINE
- Fluid flows
- Incompressible
- No viscosity
- Euler works!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Euler Equations
Definition:
Equations that describe the motion of an incompressible and non-viscous fluid.
-
Term: Irrotational Flow
Definition:
Flow in which the fluid has no rotation or vorticity.
-
Term: Velocity Potential Function
Definition:
A scalar function whose gradient gives the velocity field of an irrotational flow.
-
Term: NavierStokes Equations
Definition:
A set of equations that describe how the velocity field of a fluid evolves over time.
-
Term: Viscous Flow
Definition:
Flow in which the viscosity of the fluid is significant and cannot be neglected.