Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Velocity Potentials
Unlock Audio Lesson
Good morning class! Today we are introducing velocity potentials, which are scalar functions that help us understand the velocity fields in fluid mechanics. Can anyone tell me what a scalar function is?
Is it a function that has only magnitude and no direction?
Exactly! A scalar function, such as a velocity potential, represents quantities with only magnitude. Now, can someone explain how we derive velocity components from a potential function?
We take partial derivatives of the potential function with respect to each spatial dimension!
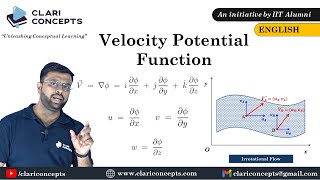
Right! We have u = ∂φ/∂x, v = ∂φ/∂y, and w = ∂φ/∂z. This relationship will be crucial as we solve fluid problems. Remember: 'Velocity peaks from potential speaks!' It’s a mnemonic to help you recall how to derive velocities from potentials.
What does it mean for a flow to be irrotational?
Good question! A flow is irrotational when there are no vorticities, meaning the curl of the velocity vector is zero: ∇ × v = 0. This is essential for using velocity potentials.
Can you give an example where we might use velocity potentials?
Sure! One example is fluid flow between fixed and moving plates. We'll explore that as we continue. To summarize: Velocity potentials simplify our analysis in fluid mechanics, provided the flow is irrotational.
Conditions for Using Velocity Potentials
Unlock Audio Lesson
Let’s focus now on the conditions required for applying velocity potentials. Can anyone recall what the main condition is?
It has to be irrotational flow, right?
"Exactly! In irrotational flow, vorticities are negligible. This can often be analyzed by checking if
Relationship Between Streamlines and Velocity Potentials
Unlock Audio Lesson
Now we dive into the relationship between streamlines and velocity potentials. What do we know about their intersection?
They intersect at right angles!
Correct! This orthogonality is crucial in simplifying flow visualizations. It helps to map out potential flow fields easily. Can anyone relate this back to our earlier conversations about flow behavior?
So it shows how these functions represent different aspects of flow fields, with streamlines indicating motion and potentials showing energy states?
Exactly! 'Streamlines show flow designs, potentials scope energies' is a mnemonic to connect these two concepts. Why do you think this orthogonality is beneficial for fluid analysis?
Because it gives us a clearer picture of overall flow characteristics and helps us verify our analysis!
Absolutely! It enhances both theoretical calculations and practical applications in fluid dynamics. As we proceed, always think about how orthogonality helps visualize and determine flow behaviors.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section covers the concept of velocity potentials in fluid mechanics, explaining how they relate to scalar velocity fields in irrotational flows. It details the derivation of key equations and conditions under which these potentials can be applied, along with examples of flow scenarios.
Detailed
Introduction to Velocity Potentials
In this section, we delve into the concept of velocity potentials, a key tool in fluid mechanics that simplifies the analysis of fluid motion under specific conditions. Velocity potential functions are scalar functions from which the velocity vector of an incompressible, irrotational flow can be derived. This simplification is particularly useful because it reduces the complexity of solving fluid equations.
Key Points Covered:
- Velocity Potentials: Defined as scalar fields from which velocity components can be derived using partial derivatives. The relationship is established as follows:
-
Velocity Components:
- u = ∂φ/∂x
- v = ∂φ/∂y
- w = ∂φ/∂z
This relationship highlights how velocity potentials incorporate spatial and temporal variations in an irrotational flow.
- Conditions for Application: Velocity potentials can only be applied in irrotational flow conditions where vorticities are negligible. This is mathematically expressed by the condition
-
∇ × v = 0
which establishes a one-to-one relationship with the potential function. - Flow Analysis: The section also discusses applications of these functions through examples, such as flow between fixed and moving plates, and how to use Equi-Potential and Streamline lines effectively in such contexts.
- Orthogonality: The relationship between velocity potential functions and stream functions is explored, emphasizing their orthogonality—where equipotential lines and streamlines intersect at right angles—facilitating the visualization of velocity fields.
This foundational section provides essential insights into the utility of velocity potentials in analyzing fluid flows, bridging the theoretical aspects of fluid dynamics with practical problem-solving techniques.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Velocity Potentials
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So that way let me go through the basic things what we discussed that basically we are going to introduce velocity potentials okay. I will discuss more details.
Detailed Explanation
Velocity potentials are mathematical functions that simplify the analysis of fluid flows, particularly in irrotational flow. They serve to express the velocity vector field in a scalar form, making equation manipulation easier.
Examples & Analogies
Think of velocity potentials like a map that can show multiple routes at once. Just like a map can help you see the best path to take without needing to traverse each route actively, velocity potentials allow us to understand fluid movement efficiently without individually calculating all velocity components.
Defining Velocity Potentials
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The basic idea comes that can you write these equations with a single scalar value okay that is the simple idea comes is that instead of looking at 3 scalar velocity component why we cannot write it with a simple a scalar functions that is what is the velocity potential function.
Detailed Explanation
Instead of dealing with three components of velocity: u, v, and w, which can complicate calculations, a single scalar function known as the velocity potential function (denoted as phi) can represent the flow field. The velocity vector can then be expressed as the gradient of this scalar function.
Examples & Analogies
Imagine trying to explain the weather across different areas. Rather than giving detailed data for temperature, wind speed, and humidity for each point, you can summarize it using a weather map that shows different zones. In this analogy, the weather map represents the velocity potential function that simplifies the explanation of the flow.
Irrotational Flow Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus if I define it the velocity is a gradient of phi, phi is a velocity potential function at which condition thus this is what justified it was.
Detailed Explanation
For velocity potentials to be applicable, the fluid flow must be irrotational. This means there are no vortices or rotational effects in the flow. One way to determine if a flow is irrotational is to check if the curl of the velocity vector field is zero.
Examples & Analogies
Think of a smooth lake on a calm day. The water flows in a straight line without any turbulence or swirls—this represents irrotational flow. Contrast this with a river with rapids or whirlpools, where the flow is rotational and the concept of velocity potentials would not apply.
Applications of Velocity Potentials
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So you should try to understand it very detailed way how what should be the streamlines what with the velocity potential functions where we expected it there is a formations of boundary layers because of no slip conditions of net to the structures.
Detailed Explanation
Velocity potentials are used to analyze flow patterns and predict behavior near boundaries, such as surfaces of objects in the fluid. They help us understand phenomena like boundary layers—regions where the fluid velocity changes from zero (due to the 'no-slip' condition against the surface) to the free-stream velocity.
Examples & Analogies
Imagine a car moving through air. The air closest to the car's surface sticks to it (no-slip condition), while the air farther away moves freely. Analyzing the flow using velocity potentials can help us predict how the air behaves and interacts with the car, optimizing its design for better aerodynamics.
Orthogonality of Streamlines and Potential Lines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The only things is difference here that the stream functions exist for two-dimensional cases okay.
Detailed Explanation
In fluid dynamics, streamlines and equipotential lines (lines representing constant potential) are orthogonal to each other in irrotational flow. This means where they intersect, they do so at right angles. The relationship helps visualize the flow and determine flows' characteristics.
Examples & Analogies
Think of walking along a grid in a city. The streets represent streamlines, and the alleys represent potential lines. At every intersection, you can see how they cross at right angles, helping you navigate through the city. This orthogonality simplifies understanding how fluids behave in different conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Velocity Potentials: Scalar functions that simplify the analysis of flow fields.
-
Irrotational Flow: Essential condition that permits the use of velocity potentials in flow analysis.
-
Stream Function: Related function that represents the flow field lines orthogonally to velocity potentials.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When analyzing fluid flow around a cylindrical object, the use of velocity potentials can simplify calculations related to pressure and velocity fields.
-
In a system where two plates are fixed and a fluid flows between them due to pressure gradients, velocity potentials can aid in understanding how flow varies across the gap.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find the velocity field, take phi's path, differentiate each way to avoid the math wrath!
📖 Fascinating Stories
-
Imagine a river flowing smoothly toward the sea (irrotational). If a boulder is placed, it creates eddies, illustrating what happens in turbulent flows where velocity potentials can't apply.
🧠 Other Memory Gems
-
IRR means Incomprehensible Rocks Rotate; remember this to connect irrotational flow and vorticity!
🎯 Super Acronyms
POT
- Potential's Orthogonal to Timing helps remember the flow patterns are both dependent on potentials and their interactions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Velocity Potential
Definition:
A scalar function from which velocity components of a flow field can be derived via gradients.
-
Term: Irrotational Flow
Definition:
A flow condition where the vorticity is zero, allowing for the application of velocity potentials.
-
Term: Stream Function
Definition:
A mathematical function used to describe flow field lines, orthogonal to velocity potentials in two-dimensional flows.
-
Term: Vorticity
Definition:
A measure of rotation in a fluid flow, indicated by the curl of the velocity field.