Enrol to start learning
Reading is open to everyone. Enrolling is free, and it is what unlocks the audio lessons, practice tests and progress tracking.
10.5. Lec 31: Approximate Solutions of Navier-Stokes Equation: Boundary Layer Approximation
Learn content
Interactive Audio Lesson
Unlock the classroom podcast
The transcript is free to read. A free account plays the conversation back.
Today, we are diving into the Navier-Stokes equations and how they can be approximated for simpler calculations. Can anyone tell me why we often need these approximations in fluid mechanics?
Because the full equations can be really complex and hard to solve directly?
Exactly! The complexity of the Navier-Stokes equations can make them practically impossible to solve analytically for most flows. By using approximations, such as the boundary layer approach, we simplify our calculations significantly. This is crucial in engineering applications.
So how do we determine when to use these approximations?
Great question! We often look for conditions like steady flow, incompressible fluids, and situations where viscous effects dominate. We'll explore this further.
To remember this, think of 'SIV' — steady, incompressible, viscous. These are key conditions for applying boundary layer approximations!
Is the boundary layer concept only applicable to specific geometries?
Mostly! It's commonly applied around flat plates, but we can also see it in cylindrical geometries and around other solid structures.
In essence, approximations aren't merely shortcuts; they're necessary tools in fluid dynamics that allow us to analyze complex behaviors effectively. Let's summarize: we've established why we need approximations and the conditions under which we can use them.
Unlock the classroom podcast
The transcript is free to read. A free account plays the conversation back.
Now that we understand the need for approximations, let’s focus on boundary layers. What is a boundary layer?
I think it's the region where viscous effects are significant due to the presence of a solid surface?
Correct! Within the boundary layer, viscosity alters the velocity of the flowing fluid close to a solid surface. Outside the boundary layer, the flow could be modeled as inviscid or less affected by viscosity.
So, how do we define where the boundary layer starts and ends?
Nice inquiry! The boundary layer begins at the leading edge of the surface and extends to where the flow velocity approaches the free stream velocity. This typically establishes its thickness based on the flow conditions.
And the boundary layer is different in laminar and turbulent flows, right?
Absolutely! In laminar flow, it's smooth and thinner compared to turbulent flow, where it behaves more chaotically and is thicker. Remember: 'LT' — Laminar Thin, Turbulent Thick. Let’s recap: the boundary layer defines the region of influence from a surface due to viscosity.
Unlock the classroom podcast
The transcript is free to read. A free account plays the conversation back.
Let's apply what we've learned to problems involving fixed and moving plates. What happens to the flow when a plate moves?
The fluid near the plate will acquire its velocity, while the fluid further away remains unaffected?
Exactly! This velocity gradient between different layers creates shear stress. For a moving plate, we say there’s a velocity profile that can be linear under certain assumptions.
How do we derive the velocity profile in these situations?
We simplify the Navier-Stokes equations under the assumptions we've discussed. By accounting for steady flow and neglecting certain terms, we can derive a simple linear velocity profile between plates.
What about pressure gradients? Do they affect the flow too?
Great point! Pressure gradients can also drive flow, especially when considering cases like flow between two fixed plates where we calculate velocity distribution due to a pressure drop.
To summarize this session: understanding the role of shear stress and pressure gradients in flow profiles between plates is crucial for analyzing fluid behavior in many applications.
Unlock the classroom podcast
The transcript is free to read. A free account plays the conversation back.
In discussing approximations and boundary layers, we mention velocity potential functions. What are these?
Are they functions that help define flow fields in irrotational flows?
Exactly! They allow us to define fluid flow fields using a single scalar function, simplifying our calculations. This can be especially useful for irrotational flows.
Why do we need to consider irrotational flow when using these functions?
That's because velocity potential functions only apply when the flow has negligible vorticity, which is a condition we must ensure.
Does this relate back to the boundary layer we discussed?
Yes! In boundary layers, we may encounter rotational flows due to shear. Thus, care must be taken when applying velocity potential functions in these regions.
To recap this session: velocity potential functions are powerful tools in fluid mechanics, but must be applied with an understanding of the flow characteristics, especially regarding rotational effects.
Unlock the classroom podcast
The transcript is free to read. A free account plays the conversation back.
To sum up all we've discussed, how do we integrate these approximations in real-world applications?
By recognizing when boundary layers form and simplifying the Navier-Stokes equations accordingly?
Correct! Knowing these conditions helps engineers design better systems and predict fluid behavior in applications like aerospace and mechanical engineering.
So, concluding simplifications is key to applying theoretical knowledge practically?
Absolutely! By utilizing boundary layer approximations and understanding their limitations, we can make intelligent predictions in real-world scenarios.
Let’s summarize: today we've established the critical interplay between theory and application in fluid mechanics through the lens of Navier-Stokes approximations.
Overview
Short Summary
This section explores approximate solutions to the Navier-Stokes equations specifically focusing on the boundary layer approximations.
Medium Summary
The section provides an overview of approximating the Navier-Stokes equations for simple flow problems, detailing the derivation and application of boundary layer approximations in fluid mechanics. Key topics include analyzing incompressible viscous flows between moving and fixed plates, and understanding velocity potential functions.
Detailed Summary
Approximate Solutions of Navier-Stokes Equations: Boundary Layer Approximation
In this section, we delve into the methods for deriving approximate solutions to the Navier-Stokes equations, which govern fluid flow. We focus specifically on boundary layer approximations, a critical concept in fluid mechanics that simplifies the analysis of flow near objects.
Starting with existing knowledge from previous lectures on velocity potential functions, this section emphasizes the significance of these approximations in solving flow problems involving fixed and moving plates as well as through cylindrical geometries.
Key points covered include:
- The distinction between irrotational flows where velocity potential functions can be applied, versus the scenarios where boundary layers exist due to viscous effects or flow separation.
- Deriving and simplifying the Navier-Stokes equations under specific assumptions, enabling the transition from complex partial differential equations to manageable ordinary differential equations (ODEs).
- Exploration of velocity distribution functions around moving plates and the resulting shear stresses derived from pressure gradients.
- Techniques for calculating flow fields, including steady flow conditions and the constant density assumptions for incompressible fluids.
Through examples and analysis of pressure and velocity distributions between two fixed plates, as well as boundary layer formations, the section emphasizes the practical applications and importance of understanding fluid flows in various engineering contexts.
Reference YouTube Videos
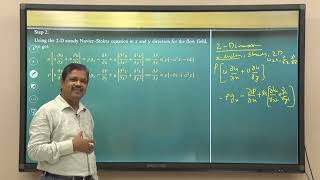
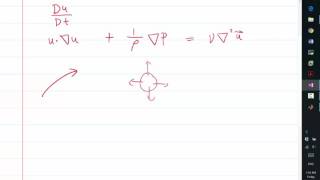
Audio Book
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountGood morning all of you. Today we are going to discuss about approximation solutions of Navier-Stokes equations. That is what we earlier you started to how to approximate the Navier-Stokes equation for simple problems flow through two plates with movable plate with pressure gradient.
Detailed Explanation
In this chunk, the professor sets the stage for the lecture by introducing the key topic: the approximation of Navier-Stokes equations. These equations are fundamental to fluid mechanics and describe how fluids move. Approximating them allows us to find solutions for simpler fluid dynamics problems, such as flow between plates or through pipes. By focusing on specific cases, it becomes manageable to derive useful equations that can predict fluid behavior under different conditions.
Examples & Analogies
Imagine you are baking cookies. The complete recipe involves many steps, but for a quick batch, you might simplify by mixing ingredients in one bowl instead of measuring everything separately. Similarly, approximating Navier-Stokes equations allows engineers to simplify fluid flow problems and get quick, actionable insights.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountSame way we can look it for solutions of Navier-Stokes equations for pipe flow through a concentrated cycles circles we can do that. But today we will solve to problems, mathematical problems, then we will discuss about the boundary layer approximations for Navier-Stokes equations.
Detailed Explanation
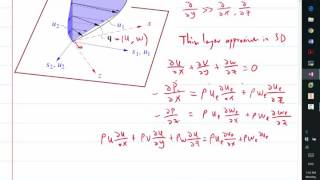
This section emphasizes the focus on boundary layer approximations, key in fluid dynamics when examining how fluids interact with surfaces. The boundary layer is a thin region near a surface where effects of viscosity are significant. These approximations simplify the Navier-Stokes equations, enabling the analysis of flow in common scenarios like pipes or around objects. This helps in analyzing the behavior close to surfaces, crucial for designing efficient systems in engineering.
Examples & Analogies
Think about the way a river flows past a rock. The water closest to the rock moves slower due to friction (the boundary layer), while the water farther away flows faster. Understanding this difference helps civil engineers design bridges and dams more effectively, allowing for safe and efficient water management.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
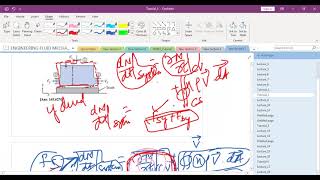
Create a free accountThe problem is that there is a steady again I am emphasizing two-dimensionals incompressible velocity field is given to us. We have to compute a functions pressure is a function of x and y okay.
Detailed Explanation
In this part, the professor introduces a problem involving a steady two-dimensional incompressible velocity field. Students are tasked with determining the pressure field as a function of x and y. The problem is structured to require the application of the continuity equations alongside the Navier-Stokes equations to ensure that the derived pressure field is physically valid and consistent with the given velocity field.
Examples & Analogies
Imagine you're trying to predict the pressure in a water hose that bends. The pressure at different points in the hose depends on how fast the water is moving and where the hose is curved. By understanding how the water flows (the velocity field), you can predict how much pressure is needed at each point to keep the water flowing smoothly without bursting the hose.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountIf you look at that the velocity field what is given to us which is having the scalar component in x directions Ax b, this is u functions and you have minus Ay plus Cx j functions okay. So this is the u component and this is the v component.
Detailed Explanation
This section involves analyzing the given velocity components represented mathematically by equations in both x and y dimensions. By checking these components against the continuity equation—which states that the sum of fluid entering a region must equal the sum exiting—it can be confirmed whether the provided velocity field is valid. This validation is essential before proceeding to pressure calculations, ensuring the flow is physically plausible.
Examples & Analogies
Think of a water slide that starts wide but narrows down. At the wide part, lots of kids can go in at once, but as it narrows, the same number of kids must pass through—ensuring that no one gets stuck. The continuity equation is like the rule that maintains the balance of kids sliding down, just like fluid flow must balance itself to maintain steady conditions.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountIf the velocity field does not satisfy the continuity equation, we should not find out the pressure field for that.
Detailed Explanation
Here, the professor highlights the critical validation step again—the velocity field must satisfy the continuity equation before one can derive the pressure field. If the continuity condition isn't met, it indicates an inconsistency or a physically impossible scenario, meaning proceeding with pressure calculations would yield invalid results. This reinforces the importance of foundational principles in fluid mechanics.
Examples & Analogies
Imagine trying to fill a balloon while simultaneously letting air out—the volume of air inside must continuously adjust. If the air is escaping faster than you can pump it in, the balloon will never inflate properly. Similarly, if the continuity equation is not satisfied, our calculations for pressure won't accurately reflect the realities of fluid flow.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountIf continuity equations are not satisfied we could stop here because it is not a given field could not be a physically possible okay that is try to understand it.
Detailed Explanation
This chunk reiterates the necessity of verifying the continuity equation before proceeding to compute the pressure field. If the velocity field fails this test, any attempts to calculate pressure become irrelevant. Understanding and ensuring consistency with the key principles of fluid flow ensures meaningful results in engineering applications.
Examples & Analogies
It's like planning a party: if you don't know how many guests are coming (the flow's consistency), your plans for food and space won't work. If your calculations for pressure lack a valid velocity field, they’re equally destined for failure.
--
Key concepts
Core takeaways and short definitions to help you quickly recall the key ideas from this section.
- Navier-Stokes Approximation:
Simplifying complex equations for practical calculations.
- Boundary Layer:
The significant region close to surfaces where viscosity affects flow.
- Velocity Potential Functions:
Scalar functions simplifying flow analysis for irrotational flows.
Examples
Memory aids
In layers close to a plate, The viscous flow will resonate. With velocity thin and bright, The boundary layer is our sight.
Imagine a flat plate in a river. The water close to the plate moves slower than the water further away. This slower-moving water creates a 'boundary layer' where viscosity changes things. Knowing this helps engineers design better ships!
To remember key concepts: 'Navy BvI' - Navier-Stokes, Boundary Layer, Velocity Potential, and Irrotational flow.
Flash Cards
Glossary
Navier-Stokes Equations
A set of equations describing the motion of fluid substances, accounting for viscosity, pressure, and other forces.
Boundary Layer
The region of fluid near a solid surface where viscous effects significantly influence flow behavior.
Velocity Potential Function
A scalar function from which the velocity field of an irrotational flow can be derived.
Irrotational Flow
A flow where the vorticity is negligible, allowing the use of velocity potential functions.
Viscous Flow
Flow where viscosity effects are significant, often seen in boundary layers.