Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Flow Problems
Unlock Audio Lesson
Good morning everyone! Today, we're going to explore simple flow problems. What do you think makes flow problems 'simple'?
Maybe because they don't involve complex variables like turbulence or compressibility?
Exactly, Student_1! Simple flow problems typically involve incompressible fluids, allowing us to apply basic equations. Can anyone name one such equation?
Bernoulli's equation?
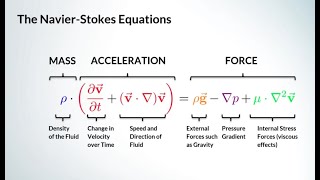
Correct, Student_2! Bernoulli's principle is a foundational concept, which we derive from the Navier-Stokes equations. Does anyone remember what the Navier-Stokes equations account for?
They account for viscosity and pressure within fluid flow?
Right! Viscosity plays a crucial role in how fluids behave in motion.
Velocity Potential Functions
Unlock Audio Lesson
Now, let's talk about velocity potential functions. Can anyone explain how they simplify our calculations?
I think they allow us to convert vector equations into scalar equations?
Exactly, Student_4! When we define velocity as the gradient of a potential function, we can reduce the complexity of solving fluid equations. Why do you think this is beneficial?
It makes it easier to find the velocity field without dealing with multiple variables!
Exactly! It lets us determine flow velocities using one scalar function. Remember, this is only valid under irrotational flow conditions.
Effects of Pressure Gradients
Unlock Audio Lesson
Let's now look at pressure gradients. How do you think these gradients influence fluid velocity?
If there's a pressure difference, it can accelerate the fluid, right?
That's correct! A higher pressure at one end will push the fluid to the lower pressure zone, creating flow. Can you think of a practical example?
Like water flowing out of a faucet when I open it?
Exactly. The faucet creates a pressure drop, which drives the water out.
Streamlines and Equipotential Lines
Unlock Audio Lesson
Now, let's look at streamlines and equipotential lines. Why are they important in fluid mechanics?
They help visualize the flow patterns and identify areas of velocity change.
Great observation, Student_4! Their orthogonality means that wherever they cross, the angle formed is 90 degrees, which indicates the nature of flow in that area.
So knowing both helps us understand both the velocity field and the pressure field simultaneously?
Absolutely correct! This comprehensive understanding is essential for applications in engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the derivation of equations governing incompressible viscous flow, including Bernoulli's principles linked to the Navier-Stokes equations. We discuss specific flow scenarios, including flow between fixed and moving plates, and the role of velocity potential functions in simplifying these complex problems.
Detailed
Simple Flow Problems and Pressure Gradient Effects
In this section, we delve into the fundamental concepts of fluid mechanics focusing on simple flow problems and the impact of pressure gradients. We begin by recapping the derivation of Bernoulli's equations from the Navier-Stokes equations, linking the mathematical foundation of fluid mechanics to practical applications. Through various examples, we illustrate how to analyze incompressible viscous flows, which include flows between a fixed and a moving plate as well as flows impacted by pressure gradients.
We introduce the concept of velocity potential functions, which simplify the complexity of fluid flow equations, allowing for easy derivation of flow characteristics. The section emphasizes conditions under which these equations can be applied, particularly stressing the significance of irrotational flow for the applicability of velocity potential functions. The interrelationship between streamlines and potential lines is also discussed, highlighting their orthogonality in two-dimensional flows. This comprehensive exploration aids in understanding how pressure gradients affect velocity distributions in diverse systems, providing students with foundational knowledge in fluid dynamics that can be applied to various engineering scenarios.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Velocity Potentials
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As we discussed in the last class how we can derive the basic Bernoulli's equations from Navier-Stokes equations that what we did it Navier-Stokes equations from that we derived Euler equations then we have derived Bernoulli's equations. So that components also today I will recap it then we will go through these today topics which mostly I am following it the book of F M White fluid mechanics books for today lectures.
Detailed Explanation
In fluid mechanics, understanding how fluid flows and behaves under various conditions is crucial. The lecturer recaps the insights gleaned from previous discussions, especially the derivation of Bernoulli's equations from the Navier-Stokes equations, which are fundamental equations governing fluid flow. Through the analysis of these equations, we can understand different flow behaviours, focusing on how potential function concepts simplify these complex equations into more manageable forms.
Examples & Analogies
Think of a river flowing over a series of rocks. Just like the flow of water changes depending on the rocks, in fluid mechanics, the flow dynamics change depending on the equations derived from fundamental principles like the Navier-Stokes and Bernoulli's equations.
Velocity Potential Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The basic idea comes that can you write these equations with a single scalar value okay that is the simple idea comes is that instead of looking at 3 scalar velocity component why we cannot write it with a simple a scalar functions that is what is the velocity potential function.
Detailed Explanation
The velocity potential function is an important concept in fluid mechanics used to simplify the analysis of flow fields. In traditional fluid dynamics, we usually consider three components of velocity (u, v, w). However, by using a single scalar function known as the velocity potential function (φ), we can represent these components as gradients, which makes calculation easier. This is particularly useful in situations where flow is irrotational, allowing us to reduce complexity in fluid analysis.
Examples & Analogies
Imagine you are navigating a complex maze. Instead of tracking every twist and turn (which represents the three velocity components), you could use a series of signs to point directly towards the exit (the velocity potential function), which simplifies your journey significantly.
Conditions for Irrotational Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus if I define it the velocity is a gradient of phi, phi is a velocity potential function at which condition thus this is what justified it was. If you look at the very basic components if I velocity potentials.
Detailed Explanation
For the velocity potential function concept to work effectively, the flow must be irrotational, meaning there can be no rotation or swirling motion in the fluid elements. This condition allows us to express velocity as the gradient of a scalar potential function. If the flow has irrotational characteristics, we can make significant simplifications in deriving solutions and analyzing flow patterns, making the analysis much easier and more intuitive.
Examples & Analogies
Consider how water flows out of a garden hose when you point it straight out. The water flows smoothly without swirling. In this case, the flow can be treated as irrotational. If you were to twist the nozzle, creating turbulence, this would no longer be an irrotational flow, complicating the analysis significantly.
Understanding Streamlines and Velocity Potential Lines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The same way if I can draw I can draw the streamlines I can draw the velocity potential line. The only things is difference here that the stream functions exist for two-dimensional cases okay.
Detailed Explanation
In fluid dynamics, streamlines are lines that represent the direction of flow at every point in a fluid. Velocity potential lines, on the other hand, indicate where the potential function is constant. These two types of lines typically intersect at right angles in irrotational flow, showcasing the relationship between the velocity and the potential function. Understanding these concepts allows us to visualize and analyze where and how fluid flows in various scenarios.
Examples & Analogies
Think of streamlines as the paths of people flowing through a crowded train station. The velocity potential lines are like the signs giving directional information. Where there’s a sign pointing in one direction (potential line), it often intersects with crowded paths (streamlines) at angles, indicating they affect each other's flow patterns.
Implications of Viscosity and Rotational Flows
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Same concept is here instead of the laws of motions here we talk about the rotations that means if the flow field is irrotational okay.
Detailed Explanation
The concept of viscosity and rotational flow is critical in fluid dynamics. Just as Newton's first law states that an object remains at rest or in uniform motion unless acted upon by an unbalanced force, the flow of fluids behaves similarly. In rotatory flow (caused by viscosity or external disturbances), predicting flow characteristics becomes complex as rotational movements produce vorticity, separating the flow from the ideal simplifications provided by potential functions.
Examples & Analogies
Imagine driving a car on a straight road at a constant speed (irrotational flow) — you maintain your direction. But if you hit a patch of ice (viscous disturbance), your car may start spinning out of control, showing how disturbances can affect the overall behavior of the flow in unpredictable ways.
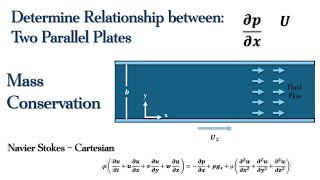
Pressure Gradients and Flow between Plates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look at very interesting part which I can relate it with very basic equations what you know it is the Newton's first law of motions is you know it if you look at that Newton's laws first law of motions okay you know with the three laws okay.
Detailed Explanation
Understanding pressure gradients is essential in analyzing fluid flow, particularly between two plates. The concept asserts that the difference in pressure between locations can drive the flow of the fluid within the channel between the plates. This scenario highlights how pressure differences and flow velocity interact, influencing the fluid's characteristics and behavior.
Examples & Analogies
Think of a water slide. At the top of the slide, there's a lot of pressure due to gravity. As you slide down, this pressure changes and creates a rush of water flowing down the slide. Similarly, in fluid mechanics, pressure differentials can cause the fluid to move between two plates, just like you sliding down the hill.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Simple Flow Problems: These often involve analyzing incompressible fluids and apply simpler mathematical models.
-
Bernoulli's Principle: A fundamental equation derived from the conservation principles in fluid mechanics.
-
Velocity Potential Functions: A simplified approach to represent velocity distributions in fluid flow.
-
Pressure Gradients: Differences in pressure across a fluid that drive flow.
-
Streamlines and Equipotential Lines: Visual tools that help in understanding fluid motion and pressure distributions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Water flowing between two parallel plates under a pressure gradient.
-
Airflow around a building demonstrating pressure differences.
-
The flow of oil in a pipeline, illustrating viscous effects.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In flows that stay the same, pressure drives the game, from high to low they fly, as streamlines draw the eye.
📖 Fascinating Stories
-
Imagine a river; where the banks create pressure differences, water flows swiftly from high to low, guiding fish downstream.
🧠 Other Memory Gems
-
PEVS - Pressure creates Energy Velocity Streamlines.
🎯 Super Acronyms
SLE (Streamline, Velocity potential, Equipotential line) - Helps remember the flow concepts.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Incompressible Flow
Definition:
A type of fluid flow where the density of the fluid remains constant.
-
Term: Viscous Flow
Definition:
A type of flow that accounts for viscosity effects in the fluid.
-
Term: Velocity Potential Function
Definition:
A scalar function whose gradient gives the velocity vector of the flow.
-
Term: Pressure Gradient
Definition:
The rate of change of pressure in a fluid flow direction, influencing flow velocity.
-
Term: Streamline
Definition:
A line that is tangent to the velocity vector of the flow at every point.
-
Term: Equipotential Line
Definition:
A line along which the potential function has a constant value.