Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Irrotational Flow
Unlock Audio Lesson
Good morning, class! Today, we are diving into the concept of irrotational flow. To start, can anyone tell me what they think irrotational flow means?
Is it the flow where the fluid has no vorticity?
Exactly! Irrotational flow is defined by the absence of rotation in fluid elements. This means that the velocity field can be described entirely with a potential function. Remember the term 'vorticity' as it relates directly to flow characteristics.
So, when do we consider a flow to be irrotational?
Great question! Generally, we consider a flow to be irrotational if the vorticity, or the curl of the velocity field, is zero. This leads us to the use of velocity potential functions.
What are velocity potential functions, though?
Velocity potential functions are scalar functions from which we derive the velocity field through its gradient! They simplify the analysis of fluid motion.
So does that mean we don't have to worry about all three velocity components anymore?
Precisely! Instead of dealing with u, v, and w, we can just work with the potential function. This greatly simplifies our calculations.
So, to summarize this session: irrotational flow means no vorticity and allows us to use velocity potential functions for analysis, simplifying our equations.
Conditions for Using Velocity Potential Functions
Unlock Audio Lesson
Now that we've understood irrotational flow, let’s explore the conditions required to apply these velocity potential functions. Who remembers!
The flow must be irrotational!
And it should ideally be incompressible, right?
Correct! Flow must ideally be incompressible, and there should be negligible rotational activity. Without these conditions, velocity potential functions may not yield accurate results.
Does that mean we have to check these conditions every time we analyze flow?
Yes! It's essential to verify these conditions, particularly in engineering applications like calculating flow around buildings, where rotational effects and vorticity can become important.
What if the flow is not irrotational?
Good question! If the flow isn’t irrotational, we’d have to revert to the full Navier-Stokes equations, which account for viscosity and turbulence.
To summarize, we can use velocity potential functions under conditions of irrotational and incompressible flow with negligible rotational activities.
Linking Theory with Applications
Unlock Audio Lesson
Now, let's apply what we learned! How do we analyze flow past tall buildings using irrotational flow concepts?
We can draw streamlines and identify potential functions!
Exactly! By visualizing streamlines, we observe flow patterns. How about the impact of buildings?
I think the flow separates around the structure?
Correct! In flow separation, the assumptions of irrotationality can break down. We often face complexities which require detailed analysis.
So in practical applications, we check for boundaries and flow regions?
Absolutely! Understanding the boundaries is critical. We can utilize computational simulations, but the foundation learned today is crucial in making these computations effective.
To summarize, recognizing how to visualize flow patterns and understand separation enhances our ability to analyze real-world applications of fluid dynamics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section highlights the significance of irrotational flow in fluid mechanics, explores the derivation of velocity potentials, and outlines the conditions under which these potentials can be applied, emphasizing the physical implications related to fluid flow behavior.
Detailed
Irrotational Flow and Conditions
This section elaborates on irrotational flow, a key concept in fluid mechanics characterized by a flow field where the rotation of fluid elements is negligible. The section first revisits the foundational equations derived from the Navier-Stokes equations, specifically focusing on Euler's equations for incompressible and non-viscous flow. It introduces the concept of velocity potential functions, explaining how these functions simplify the representation of a velocity field by replacing multiple scalar velocity components with a single scalar potential.
The discussion highlights the conditions needed for velocity potential functions to be valid, notably that the initial flow must be irrotational. The section explains the mathematical rigorousness behind this requirement, detailing how the gradient of the velocity potential equates to the flow velocity and under what boundary conditions these relationships hold true.
The section culminates in emphasizing the practical applications of this theory in dealing with real-world fluid problems, such as flow past structures and flow between plates, thereby linking theoretical perspectives with practical implications in civil engineering.
Youtube Videos
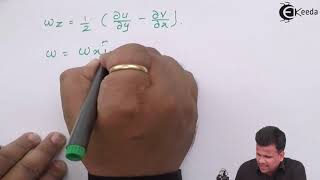
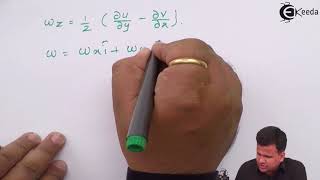
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Irrotational Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In this section, we discuss the concept of velocity potentials and their applications in fluid mechanics. Irrotational flow is characterized by the absence of vorticity.
Detailed Explanation
Irrotational flow refers to a fluid flow in which the fluid particles do not rotate about their center of mass. If the flow is irrotational, it means that the circulation around any closed loop in the fluid is zero. In such conditions, we can express the velocity field in terms of a scalar potential function, known as the velocity potential, which helps simplify calculations.
Examples & Analogies
Think of a calm lake with no wind—a small boat can glide smoothly across the surface without creating any ripples or swirls. This scenario resembles irrotational flow because the water is not swirling around, allowing the boat to move freely.
Velocity Potential Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We introduce velocity potential functions, which are analogous to electric field potentials. The velocity vector can be expressed as the gradient of the velocity potential function.
Detailed Explanation
A velocity potential function, denoted as φ (phi), allows us to express the fluid's velocity vector, V, as the gradient of this scalar function. Mathematically, this means V = ∇φ, where the gradient operator (∇) computes the partial derivatives with respect to space. This relationship simplifies the analysis of the flow, reducing the need to consider multiple velocity components separately.
Examples & Analogies
Imagine a hilly landscape—each point on the hill has a height value (like φ). If you know the height at a specific point, you can determine how steep a slope is (the velocity of water flowing down). The height map is similar to the velocity potential function, guiding the flow direction.
Conditions for Irrotational Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Irrotational flow conditions arise when the velocity potential function exists, and vorticity is negligible in the flow field.
Detailed Explanation
For a flow to be considered irrotational, specific conditions must be met: the fluid must flow smoothly without obstacles, the velocity must remain consistent, and the effects of viscosity should be minimal. Under these conditions, we can fully define the flow using the velocity potential function, allowing for much simpler mathematical treatment.
Examples & Analogies
Consider a scenario where water flows through a long, straight pipe without any bend or turns. The flow remains uniform, and there are no swirls or rotations in the water. This represents an ideal irrotational flow where potential functions can accurately describe the velocity field.
Orthogonality of Streamlines and Potential Lines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This section explains how streamlines and equipotential lines are orthogonal in irrotational flow, highlighting their significance.
Detailed Explanation
In an irrotational flow, streamlines (paths followed by fluid particles) and equipotential lines (lines of constant potential) intersect at right angles (orthogonal). This relationship is crucial because it means that energy remains conserved along streamlines, simplifying analysis and calculations in fluid mechanics.
Examples & Analogies
Imagine a series of crosswalks (streamlines) and sidewalks (equipotential lines) in a city. When someone crosses the street along a crosswalk, they must step off the sidewalk and into the street, illustrating the 90-degree intersection. Just like pedestrians navigate the streets, fluid particles navigate their paths defined by streamlines and equipotential lines.
Limitations and Real-World Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
While irrotational flow simplifies many fluid dynamics problems, real-world scenarios often include rotationality and turbulence.
Detailed Explanation
It is essential to recognize that not all flows are irrotational. In many practical situations, such as near solid boundaries or in turbulent flow conditions, rotational effects become significant. Understanding when to apply the concept of irrotational flow is crucial in engineering and fluid dynamics.
Examples & Analogies
Consider the smooth flow of a river. While the main body of water flows steadily (irrotational), turbulence appears near rocks or obstacles, creating swirling eddies and rotational flow. Engineers must account for these complexities when designing structures like bridges or dams.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Irrotational Flow: A flow condition without vorticity.
-
Velocity Potential Function: A simplification tool for representing velocity fields.
-
Compatibility with Euler's Equations: Understanding flow limits and conditions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Flow past a tall building can exhibit conditions of irrotational flow, except near the boundaries.
-
In analyzing incompressible flow between two plates, using velocity potential functions simplifies the analysis significantly.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If there's no whirl in the fluid's twirl, irrotational flow is the pearl!
📖 Fascinating Stories
-
Imagine a peaceful river where leaves float on top. They never spin; hence the flow is irrotational, wonderful and unbroken in its journey.
🧠 Other Memory Gems
-
Remember 'IVC' for Irrotational and Velocity Conditions to recall the criteria.
🎯 Super Acronyms
Use 'I-O-VC' for Irrotational-Only Velocity Conditions to help remember when to use potential functions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Irrotational Flow
Definition:
A flow field where fluid particles do not exhibit rotation.
-
Term: Velocity Potential Function
Definition:
A scalar function whose gradient gives the velocity vector field of the flow.
-
Term: Vorticity
Definition:
A measure of the local rotation in a fluid flow, defined as the curl of the velocity field.
-
Term: Euler's Equations
Definition:
A set of equations that describe the motion of an inviscid fluid.