Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Streamlines
Unlock Audio Lesson
Good morning class! Today we're diving into the significance of streamlines in fluid mechanics. Can anyone remind me what a streamline is?
Isn't a streamline a line that follows the direction of the flow?
Exactly! Streamlines show the path particles follow in a flow field. If we draw them, they don’t intersect. Now, what happens to the flow if the streamlines start to get closer together?
The flow speed increases, right?
That's correct! This leads us into Bernoulli's principle: where streamlines are closer together, the velocity is higher. This relationship is crucial for understanding various fluid flow scenarios.
So, streamlines also help us visualize where the flow may separate?
Right again! Now let's summarize: streamlines represent the flow direction and can indicate changes in speed and flow separation.
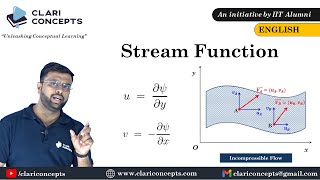
Velocity Potential Functions
Unlock Audio Lesson
Now that we understand streamlines, let’s transition to velocity potential functions. Who can explain what we mean by velocity potential?
Is it a function that helps determine the velocity at any point in the flow?
Yes! Specifically, the velocity is derived from the gradient of this potential function. For irrotational flows, this simplifies our calculations significantly. If the flow is irrotational, what can we say about the curl of the velocity?
The curl should be zero, meaning there's no rotation in the flow.
Exactly, great job! Remembering this allows us to use a single scalar function rather than three variable functions can greatly simplify our analysis.
So could we use this in practical problems? Like calculating flow near pipes?
Absolutely! It’s commonly applied in engineering to predict flow behaviors.
Applications of Streamlines and Potential Lines
Unlock Audio Lesson
Let’s talk about practical applications of our learning. How do we utilize streamlines and potential lines in real-world scenarios, like engineering?
I think we would apply it in wind flow around buildings to minimize wind resistance.
Exactly! Engineers analyze these flows to ensure buildings withstand wind forces. Furthermore, what about in fluid systems, like between two plates?
We could use these concepts to calculate viscous flow and pressure differences!
Spot on! Recognizing flow patterns helps in designing systems in a way that maximizes efficiency and minimizes energy loss.
Could turbulence affect these calculations?
Yes, turbulence complicates the flow and can break down the irrotational assumption, which is something we'll need to consider deeper in future classes.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the relationship between vector fields, streamline flows, and their corresponding velocity potential functions. It highlights the significance of Euler's and Navier-Stokes equations in understanding incompressible viscous flows, particularly in scenarios involving tall buildings and fixed plates.
Detailed
In this section, we examine the concepts of streamlines and potential lines as fundamental elements in fluid mechanics. Streamlines are defined as lines that are tangent to the velocity vector of the flow, while potential lines are related to scalar velocity potentials. We discuss how Euler's equations apply in the context of incompressible, non-viscous flows around structures such as tall buildings. Understanding velocity potential functions enables us to tackle flow problems with fewer variables, significantly simplifying the analysis. The section culminates in discussing how these principles apply to complex scenarios like flow between fixed and moving plates. We reaffirm that conditions for irrotational flow are essential for applying these concepts effectively.
Youtube Videos
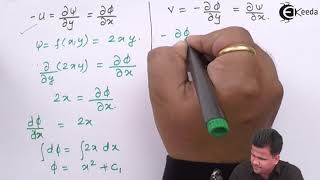
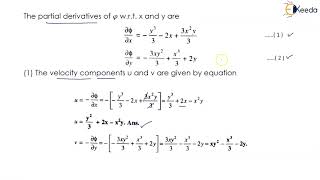
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Streamlines and Velocity Potentials
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Streamlines and potential lines are crucial concepts in fluid mechanics that help us understand fluid flow patterns. Streamlines represent the paths followed by fluid particles, while velocity potential functions allow us to express the fluid's velocity field through a scalar potential. These concepts become particularly powerful in analyzing irrotational flows, where we can reduce the complexity of our equations.
Detailed Explanation
Streamlines indicate the trajectory that fluid particles will take in a flow. When the flow is steady, the fluid's path remains unchanged. In irrotational flow, where there is no rotation in the elements of the fluid, we can define a velocity potential function, phi (φ). The velocity of the fluid can then be described as the gradient (or slope) of this potential function. This means instead of dealing with multiple components of fluid velocity, we can use a single scalar function which simplifies our calculations.
Examples & Analogies
Imagine a river. The bank of the river represents the streamlines of the flow, where each point along the bank corresponds to a point of water at that moment. If we think of the height of the river bank at various points as creating potential energy (similar to how a geologist might measure the elevation of land), that 'height' would represent our velocity potential function. The steeper the bank, the faster the water flows there. This gives us a visual analogy of how streamlines and potential functions work in fluid dynamics.
Conditions for Using Velocity Potential Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Velocity potential functions can be utilized in flows that are irrotational. The irrotational condition indicates that there is no local rotation of the fluid elements, which allows us to define the velocity field as the gradient of a scalar potential function, φ. However, in regions of flow where rotation occurs, such as near solid boundaries or in turbulent flows, the use of potential functions becomes invalid.
Detailed Explanation
To apply velocity potential functions effectively, the flow must be irrotational. In physical terms, irrotational flow means that if you could trace a small element of fluid, it would maintain a straight trajectory without spinning. This allows us to derive equations that describe the fluid's behavior without needing to account for complex lateral flows. For example, in the vicinity of a solid boundary (like the side of a moving vehicle), the fluid may exhibit rotation due to the interaction with the solid surface, and thus, the potential function cannot accurately describe the flow.
Examples & Analogies
Think of riding a bicycle on a straight road versus a windy day in a park. On the straight road (irrotational), your ride is smooth, and you can predict where you'll go based on where you steer. However, if you rode in a storm where the wind swirled around you (rotational), predicting your path becomes complicated because of the unexpected forces at play. This is akin to fluid behavior – the complexity increases significantly when the fluid interacts with objects or undergoes turbulence.
Orthogonality of Streamlines and Potential Lines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Streamlines and potential lines demonstrate orthogonality; they intersect at right angles (90 degrees). This property arises from the mathematical relationship between potential functions and stream functions.
Detailed Explanation
In fluid mechanics, the relationship between streamlines (depicted by stream functions) and velocity potential functions ensures that at their intersection, they form right angles. This orthogonality can be mathematically established: the slope of streamlines is determined by the flow velocity components and can be expressed in terms of the velocity potential. When we take the gradient of both functions, it shows that their paths will intersect perpendicularly. Understanding this property can aid in visualizing flow and predicting the behavior of fluids under various conditions.
Examples & Analogies
Think of this like a city grid where streets and highways cross at right angles. When you're planning your route, knowing that the intersections are at 90 degrees (orthogonality) allows you to make clear turns and avoid running into walls or leaving the roadway. Similarly, in fluid dynamics, understanding how streamlines (streets) intersect with potential lines (highways) in a predictable manner helps engineers visualize and design systems for effective fluid flow.
Application of Streamlines and Potential Functions in Solving Fluid Flow Problems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In practical applications, drawing streamlines and potential lines assists in analyzing fluid behavior in two-dimensional irrotational flows. Engineers can use these concepts to visualize flow patterns and apply Bernoulli’s equation effectively in various fluid dynamics scenarios.
Detailed Explanation
By drawing streamlines and potential lines, engineers can create a flow net that visually represents the fluid movement. This flow net aids in understanding how particles move through the fluid, where the high and low-pressure regions are, and helps in applying equations like Bernoulli’s equation to derive outcomes like flow velocity and pressure changes. These visual tools simplify complex fluid dynamics problems, making it easier to predict behavior and to optimize designs in various applications.
Examples & Analogies
Visualize a game of pinball. The way the ball travels through the machine can be represented by streamlines—showing its path across the board. By studying the layout of bumpers and holes (the potential paths), players can predict where the ball might go. Similarly, engineers use the concepts of streamlines and potential functions to predict the movement of fluid within pipes, ensuring systems are efficient and effective, much like scoring points in pinball!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Streamlines: Lines that trace the direction of flow and do not cross each other.
-
Velocity Potential Functions: Scalars representing the velocity fields in irrotational flows.
-
Irrotational Flow: A state where the flow does not exhibit any rotation.
-
Euler and Navier-Stokes Equations: Fundamental equations relating to fluid motion.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Visualizing the flow around tall buildings using streamlines to predict wind load and turbulence effects.
-
Calculating fluid velocities using potential functions in applications like lubrication between moving plates.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In streams of flow, lines we draw, show us the speed, that’s their law.
📖 Fascinating Stories
-
Imagine you are a river flowing past a dam. As you approach the dam, you must take a narrower path; streamlines teach us how to navigate and avoid collision!
🧠 Other Memory Gems
-
IEE for remembering that IRrotational flows lead to ENERGY Equations.
🎯 Super Acronyms
SPP - Streamlines illustrate Paths of flow, Potential functions simplify calculations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Streamline
Definition:
A line that follows the path and direction of fluid flow at any point in the flow field.
-
Term: Velocity Potential Function
Definition:
A scalar function whose gradient gives the velocity field in an irrotational flow.
-
Term: Irrotational Flow
Definition:
A flow where the curl of the velocity field is zero, indicating no rotation.
-
Term: Euler Equations
Definition:
Equations that describe the motion of inviscid fluids, applicable to flows with negligible viscosity.
-
Term: NavierStokes Equations
Definition:
Equations that govern the motion of viscous fluid substances.