Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Navier-Stokes Equations and Momentum Components
Unlock Audio Lesson
Good morning class! Today, we will explore the Navier-Stokes equations and how they relate to momentum components in viscous flow. Can anyone tell me what the Navier-Stokes equations represent?
They represent the motion of fluid substances, right?
That's correct! They are fundamental in describing how fluid velocity and pressure evolve over time. Now, when we discuss momentum in this context, what do we mean by 'momentum components'?
Do you mean the different forces acting on the fluid elements?
Exactly! The momentum components include not just velocity, but also pressure gradients and viscosity, which we will quantify mathematically today.
And are the Navier-Stokes equations applicable to all flow situations?
Good question! They are primarily used for viscous flows, while the simpler Euler equations apply to inviscid flows. Remember, fluid mechanics is all about understanding these nuances!
So we need to choose which equations to use based on the characteristics of the flow?
Exactly! Recognizing whether a flow is viscous or inviscid influences our approach in solving these equations.
In summary, understanding the Navier-Stokes equations helps us get insights into the momentum of viscous flows — a crucial part of fluid mechanics!
Velocity Potentials in Irrotational Flow
Unlock Audio Lesson
Let's dive deeper into velocity potentials and see how they simplify our calculations. Who can remind us what a velocity potential function is?
Isn’t it a scalar function that helps us describe the velocity field?
Correct! Velocity potential functions enable us to represent the fluid velocity as a gradient. This approach works under specific conditions. What can those conditions be?
It has to do with irrotational flows, right? They’re where the flow doesn't have any rotation.
Exactly, we can only use velocity potentials in irrotational flows! Here’s a mnemonic to remember: 'Irrotational Velocities Use Potential.'
That’s helpful! So applying these potentials will make some of our equations easier to manage, right?
Yes! By reducing the complexity from multiple components down to one scalar equation, we can streamline our analyses.
To summarize, using velocity potential functions is immensely helpful in fluid dynamics, provided we’re dealing with an irrotational flow!
Applications in Fluid Flow Analysis
Unlock Audio Lesson
Now, let’s relate these concepts to real-world applications. For instance, how do fluid flows around buildings demonstrate our classroom theories?
The flow patterns can show us where pressure changes might occur, and our equations can help predict those changes!
Absolutely! Recognizing flow separations is essential for determining how structures will respond to the forces applied by fluid movements.
And that’s important for engineering design, right?
Precisely! Engineers use these principles to design safer and more efficient buildings and other structures. Here’s a tip: always consider how forces interact in a fluid system.
So we really see how our understanding of viscous flow can impact real-life scenarios!
Yes indeed! It’s all about applying theoretical knowledge to practical situations. In summary, understanding momentum components in viscous flow is vital for various fields, particularly engineering!
Challenge Questions: Review of Key Concepts
Unlock Audio Lesson
Let’s recap what we’ve learned today! What are the fundamental equations we use in fluid mechanics for viscous flow?
The Navier-Stokes equations!
Correct! Now, can someone explain when we would use velocity potential functions?
When dealing with irrotational flows!
That’s right! Here’s a reflective question: why is it beneficial to transition from vector to scalar equations in fluid mechanics?
It simplifies calculations by allowing us to work with less complex equations!
Excellent! Remember, being able to simplify complex systems is essential in engineering.
To summarize, our understanding of momentum components and equations allows us to predict fluid behaviors efficiently, paving the way for effective engineering solutions!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the fundamentals of viscous flow through momentum equations. We analyze the application of Navier-Stokes equations, distinguishing between incompressible and compressible flows, and introduce the concept of velocity potential functions in three-dimensional flow. These concepts are linked to the practical analysis of fluid flow past obstacles, such as buildings.
Detailed
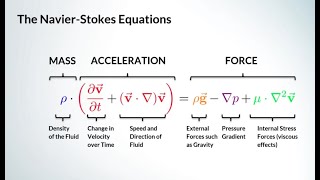
Momentum Components in Viscous Flow
In this section, we cover the essential components of momentum in viscous flow, which are pivotal in fluid mechanics. The Navier-Stokes equations are explored in depth, emphasizing their relevance for analyzing irrotational flow conditions. The section begins with a recap of the derivation of Bernoulli's equations from the Navier-Stokes equations, setting a foundation for understanding how these principles apply to real-world scenarios, such as fluid flow around tall buildings.
Key Concepts:
- Velocity Potentials: These are mathematical functions used to represent the velocity field in irrotational flow, enabling the conversion of vectorial velocity components into a scalar potential function.
- Euler Equations vs. Navier-Stokes Equations: The Euler equations apply to flows that are inviscid, while the Navier-Stokes equations accommodate viscous effects, crucial for realistic simulations of flow past structures.
- Irrotational and Rotational Flow: Definitions of these flow types are essential, as velocity potential functions can only be applied to irrotational flows, which simplifies calculations.
Practical Applications:
Understanding these concepts facilitates the analysis of complex flow situations where simplifications, like the use of potential functions, can lead to more manageable equations and solutions. This section lays the groundwork for further exploration of boundary layer theory and its implications in engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Viscous Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Good morning all of you. Today we are going to discuss on nebustic locations and its approximation for simple flow problems. We will discuss that part. As we discussed in the last class how we can derive the basic Bernoulli's equations from Navier-Stokes equations that what we did it Navier-Stokes equations from that we derived Euler equations then we have derived Bernoulli's equations.
Detailed Explanation
The introduction sets the stage for today's topic, which focuses on how to apply the Navier-Stokes equations to derive simpler forms, particularly the Bernoulli’s equations. It emphasizes the relevance of these equations in modeling viscous flows, which are critical in engineering applications. Understanding how to move from the complex Navier-Stokes equations to the simpler Bernoulli equations allows for practical calculations in fluid mechanics.
Examples & Analogies
Imagine driving a car in traffic, where you need to navigate smoothly (Bernoulli's equations) versus driving through a construction site where you must deal with barriers and obstacles (Navier-Stokes equations). Just as you simplify your route when possible, engineers simplify equations to solve problems more efficiently.
Velocity Potentials and Flow Assumptions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So basically let us start with Navier-Stokes equations which is long back about 200 years back. So the equations what we derive in last two classes we will go more detail about that. Before going that let me I just write down the basics equations is the Euler equations okay.
Detailed Explanation
This chunk introduces the fundamental equations that govern fluid flow, specifically focusing on the Navier-Stokes equations and their historical evolution. It briefly mentions the Euler equations, which are a simpler form that applies under specific conditions (inviscid flow), setting a foundation for understanding when and how these equations can be applied.
Examples & Analogies
Think of these equations like rules of the road for a driver: while some rules apply in all conditions, others only apply under ideal circumstances (like driving on a clear highway without detours). Just as a driver must know which rules to follow based on the conditions, engineers must know when to use specific flow equations.
Irrotational Flow and Velocity Potential Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The basic idea comes that can you write these equations with a single scalar value okay that is the simple idea comes is that instead of looking at 3 scalar velocity component why we cannot write it with a simple a scalar functions that is what is the velocity potential function.
Detailed Explanation
Here, the concept of velocity potential functions is introduced, suggesting a simplification where instead of dealing with three components of velocity (u, v, w), one can use a single scalar potential function (phi). This is particularly useful in flows that are irrotational, simplifying the analysis significantly.
Examples & Analogies
Imagine a river where water flows in a uniform direction; instead of tracking every droplet, you can just measure the flow level (like measuring a single variable). This simplification helps engineers predict flow behavior without getting overwhelmed by details.
Conditions for Velocity Potential Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus if I define it the velocity is a gradient of phi, phi is a velocity potential function at which condition thus this is what justified it was.
Detailed Explanation
This section emphasizes the conditions under which the velocity potential function can be applied, specifically noting that it is valid for irrotational flows. It discusses how the relationship between velocity and the gradient of the potential function can simplify the analysis of fluid motion.
Examples & Analogies
Consider a calm lake without any disturbances. Here, the surface (potential function) represents stable conditions with no unnecessary complexities. In contrast, if there’s wind (creating rotational flow), the straightforward analysis of the potential function isn’t applicable anymore.
Streamlines and Velocity Potential Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at the very basic components if I velocity potentials. v equal to grade phi is the gradient of a scalar components will be justified okay or the reverse is also true that when you have v is equal to 0 okay.
Detailed Explanation
This chunk explains the relationship between streamlines, velocity potentials, and how they interact in fluid flow. When the flow is irrotational, the velocity can be derived from the potential function, underscoring the elegance of this mathematical relationship.
Examples & Analogies
Imagine a straight river path (streamlines) through a landscape. If the river is undisturbed, you can easily predict its flow (velocity potential). However, if something interrupts the flow (like rocks), the prediction becomes complicated.
Identifying Irrotational Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
That means if I again coming back to the same flow first a tall building if I draw the two streamlines let I draw S1, S2 two streamlines...
Detailed Explanation
This section describes how to visually represent flow fields using streamlines and potential lines, emphasizing their orthogonal relationship in irrotational flow. It underlines the importance of understanding these visual tools to analyze fluid motion effectively.
Examples & Analogies
Think of sketching a winding road on a map (streamlines). The shortcuts you might take (potential lines) need to cross the road at right angles for efficient travel. Both need to be understood to navigate effectively.
Generation of Rotationality in Flows
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look at very interesting part which I can relate it with very basic equations what you know it is the Newton's first law of motions...
Detailed Explanation
The discussion transitions into how flow fields can become rotational under certain conditions, relating this concept to Newton's laws of motion. When external forces act on the fluid, the initially irrotational flow can transform into a complex rotational flow, affecting the overall behavior of the fluid system.
Examples & Analogies
Consider a spinning top (representing rotational flow) versus a balanced pencil (representing irrotational flow). The laws governing their motion describe how changes in force (like a nudge) can transition between stable and dynamic states.
Viscous Flow Dominance and Euler Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The outside of this part will show you the viscous is not dominated. That is the reasons we can use Euler equations to solve these problems...
Detailed Explanation
This chunk delineates the boundary between viscous flow and inviscid flow, explaining how and when Euler equations can be applied. It highlights the importance of recognizing flow behavior to choose the appropriate equations for analysis.
Examples & Analogies
Like choosing between two instruments in music; sometimes, you need a soft flute for gentle melodies (viscous flow analysis) or a trumpet for bold sounds (Euler physics for simpler conditions). The right choice dictates the performance.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Velocity Potentials: These are mathematical functions used to represent the velocity field in irrotational flow, enabling the conversion of vectorial velocity components into a scalar potential function.
-
Euler Equations vs. Navier-Stokes Equations: The Euler equations apply to flows that are inviscid, while the Navier-Stokes equations accommodate viscous effects, crucial for realistic simulations of flow past structures.
-
Irrotational and Rotational Flow: Definitions of these flow types are essential, as velocity potential functions can only be applied to irrotational flows, which simplifies calculations.
-
Practical Applications:
-
Understanding these concepts facilitates the analysis of complex flow situations where simplifications, like the use of potential functions, can lead to more manageable equations and solutions. This section lays the groundwork for further exploration of boundary layer theory and its implications in engineering applications.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Analysis of airflow around buildings demonstrating application of Navier-Stokes equations and identifying flow separation.
-
Using velocity potential functions to simplify calculations in irrotational flows and derive other fluid properties easily.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluids that flow without internal spin, Navier-Stokes will help you begin.
📖 Fascinating Stories
-
Imagine a river flowing smoothly without eddies, like a straight path, that's irrotational flow, calm and steady.
🧠 Other Memory Gems
-
Remember 'VIP' for Velocity, Irrotational flow, and Pressure gradients, key elements of fluid dynamics.
🎯 Super Acronyms
Use the acronym 'MOVES' to remember
- Momentum
- Ongoing flow
- Viscosity
- Equations
- and Separation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NavierStokes Equations
Definition:
A set of nonlinear partial differential equations that describe the motion of fluid substances.
-
Term: Euler Equations
Definition:
Equations governing inviscid flow, which do not account for viscosity.
-
Term: Velocity Potential Function
Definition:
A scalar function whose gradient represents the velocity field in irrotational flow.
-
Term: Irrotational Flow
Definition:
A type of flow where there is no rotation of fluid elements within the flow.
-
Term: Rotational Flow
Definition:
Flow where fluid elements exhibit rotation about their axes.