Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Rotationality
Unlock Audio Lesson
Today, we're diving into the concept of rotationality in fluids. Can anyone define what we mean by 'rotational flow'?
Isn't it when the fluid particles spin around an axis?
Exactly, rotational flow involves vorticity, which means that the fluid has a tendency to rotate. Let's contrast that with irrotational flow. Can someone share what that means?
In irrotational flow, the flow doesn't have any net rotation, right?
That's correct! Irrotational flow allows us to define a velocity potential function. Remember: 'Irrotational - No Spin, Potential - Scalar.' Let's keep this in mind as we move forward.
Navier-Stokes Equations and Velocity Potential Functions
Unlock Audio Lesson
Now, let's revisit the Navier-Stokes equations. Who can remind us why these equations are significant in fluid mechanics?
They describe the motion of fluid substances and account for viscosity.
Good! With those equations, we derive velocity potential functions under certain conditions, especially in irrotational flow. Does anyone remember how we express velocity in terms of the potential function?
It’s through the gradient of the potential function, right? Like V = ∇φ.
Precisely! This greatly simplifies our calculations. 'V = Grad φ' - remember it as 'Flow follows the potential.'
Conditions for Transitioning from Irrotational to Rotational Flow
Unlock Audio Lesson
Next, let's discuss how irrotational flow can become rotational. What factors lead to this change?
Viscous forces, right? Like when objects disturb the fluid flow.
Yes! Viscous effects from boundaries, shocks, and even turbulent wake can induce rotation. It's essential to grasp that 'Viscosity Invites Rotation.'
And it also affects the use of Bernoulli’s equation in those scenarios, doesn’t it?
Absolutely! We cannot apply Bernoulli’s principle in cases dominated by viscosity. Great connections!
Practical Implications of Fluid Rotationality
Unlock Audio Lesson
Finally, let's wrap it up with some real-world applications. Why is understanding rotational flow important?
It helps in designing better aircraft wings and other aerodynamic surfaces.
Exactly! From aerodynamics to hydraulic systems, knowing when and how rotational flow occurs can lead to improved designs. Remember: 'Flow understanding for better engineering.'
So, it's all connected! Would analyzing these conditions help us prevent flow separation?
Indeed! Managing rotational flow could mitigate separation problems. Strong conclusion!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Focusing on the Navier-Stokes equations, this section highlights the derivation of conditions for rotational flow, emphasizes the importance of irrotationality, and outlines the implications of vorticity, turbulence, and pressure gradients in various flow scenarios, notably featuring a detailed explanation of velocity potential functions.
Detailed
In this section, we explore the fundamental aspects of fluid rotationality, starting from the Navier-Stokes equations and branching into discussions about velocity potential functions, irrotational flows, and the conditions required for the transition from irrotational to rotational flows. The derivation of phenomena such as flow separation near structures and vorticity generation in the presence of boundaries is emphasized, linking physics and fluid dynamics concepts with practical implications. Through the understanding of how pressure gradients, viscous forces, and geometrical factors influence fluid flow behavior, we develop a comprehensive view of the forces at play in rotational and irrotational fluid mechanics.
Youtube Videos
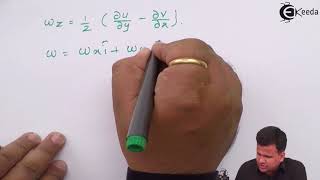
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Irrotational Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus if I define it the velocity is a gradient of phi, phi is a velocity potential function at which condition thus this is what justified it was.
Detailed Explanation
In fluid mechanics, we define a velocity potential function, denoted as phi (φ). The velocity of the fluid can be expressed as the gradient of this scalar function. This expression is used under specific conditions known as irrotational flow. Irrotational flow occurs when the flow field has no rotation, meaning that the fluid particles move in parallel layers without twisting or turning. This concept can simplify complex fluid dynamics problems significantly.
Examples & Analogies
Think of a calm lake on a windless day. The water flows in smooth layers, creating a serene surface without turbulence. This smooth, laminar flow is akin to irrotational flow, where the velocity can be expressed in terms of a velocity potential.
Condition for Using Velocity Potential Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But the conditions what we have the flow should be the irrotational flow field or the regions where the rotational activities are merely negligible.
Detailed Explanation
To utilize the velocity potential function, it is essential that the flow remains irrotational. If the flow includes significant vorticity or rotational activities, the potential function cannot accurately describe the velocity field. This means that the analysis is limited to regions where these conditions hold true, thus ensuring simplified calculations and reliable results.
Examples & Analogies
Imagine a river flowing over a smooth surface. If the riverbed is uneven, the water will swirl and create eddies, disrupting the flow. However, in a straight channel with a uniform bed, the water flows smoothly, allowing us to describe its behavior using potential functions. This analogy illustrates the importance of maintaining conditions for irrotational flow.
The Role of Boundary Layers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at that these should have had orthogonality natures that is what we are discussing it. The streamlines and the potential lines they will have a orthogonality each others.
Detailed Explanation
Understanding the relationship between streamlines and equipotential lines is vital in fluid mechanics. Streamlines represent the flow path of fluid particles, while equipotential lines are areas of constant potential energy. The orthogonality condition indicates that these two lines intersect at a right angle in irrotational flow, thus providing insights into the velocity field’s behavior and enabling easier calculations.
Examples & Analogies
Consider a roller coaster at a theme park. The track's design allows the ride to stay on course (streamlines) while the height of rails provides the energy needed for movement (potential lines). Similar to this track, the flow lines and potential lines intersecting at right angles reflect how physical forces interact in a fluid.
Conditions Causing Rotational Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If a body is remains at rest or its moves at a uniform speed in a straight line unless otherwise you all-bundle force acts on them.
Detailed Explanation
This relates to Newton's First Law of Motion, which states that an object will maintain its motion unless acted upon by an external force. In fluid dynamics, this translates to the concept of rotationality. A fluid initially in an irrotational state may transition into a rotational flow when faced with external influences like boundaries or obstacles that create turbulence or vorticity.
Examples & Analogies
Imagine riding a bicycle on a flat road. If you continue pedaling without hitting any bumps or obstacles, you maintain a straight path (irrotational flow). However, once you hit a sharp turn or a pothole, the bike wobbles, and the ride becomes less smooth, just like a fluid can become rotational when disturbed by external forces.
Significant Viscous Forces Leading to Rotational Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For examples that you have a wind movements having the uniform velocities. So when you have the uniform velocities you will not have any the nature of irrotationality is not change it unless otherwise you put a object here.
Detailed Explanation
In the context of fluid flow, significant viscous forces can disrupt the uniformity of flow and induce rotational behavior. Even a uniformly flowing wind will maintain its irrotational characteristics until it encounters an obstacle, which can create friction and boundary layers, leading to vorticity and a transitional flow state.
Examples & Analogies
Think of an open window on a windy day. The air blowing uniformly feels smooth and still (irrotational). However, when you add a curtain near the window, the air hits the curtain and starts swirling around it, creating turbulence (rotational flow). This mirrors how viscosity in a fluid flow can induce rotational effects.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Velocity Potential Function: A function whose gradient provides fluid velocity in irrotational flow.
-
Irrotational Flow: Flow that has no rotational characteristics, ideal for velocity potential application.
-
Vorticity: Indicates the tendency of elements within a flow to rotate.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Examples of rotational flow include vortices formed in turbulent rivers.
-
One can examine irrotational flow around a smooth object like a sphere to see the difference in behavior.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If you see fluids spin, that’s rotational, not just a win!
📖 Fascinating Stories
-
Imagine a river flowing smoothly over stones. It’s calm and irrotational until a rock creates whirlpools. That’s the flow changing to rotational!
🧠 Other Memory Gems
-
Remember: 'VIRs for flow types: Viscosity leads to Irrotation; Rotation is chaotic!'
🎯 Super Acronyms
IVR stands for Irrotational Viscosity and Rotation dynamics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Rotational Flow
Definition:
Flow where fluid particles exhibit rotation about their axes.
-
Term: Irrotational Flow
Definition:
Flow in which fluid particles do not rotate; described by a velocity potential.
-
Term: Vorticity
Definition:
A measurement of the local rotation in a fluid flow.
-
Term: NavierStokes Equations
Definition:
Fundamental equations describing the motion of viscous fluid substances.
-
Term: Velocity Potential Function
Definition:
A scalar function whose gradient gives the velocity of the fluid in irrotational flow.