Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Wall Shear Stress
Unlock Audio Lesson
Good morning, everyone! Today we are going to dive into wall shear stress. Can anyone tell me what wall shear stress represents in fluid mechanics?
Isn't it the force per unit area exerted by a fluid on the wall?
Exactly! It's the tangential force acting at the wall due to the flow of fluid. This is crucial for analyzing friction and the efficiency of fluid transport systems.
So, how do we calculate wall shear stress?
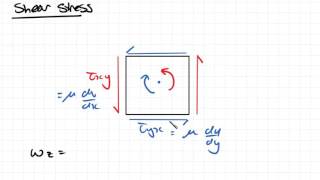
Good question! Wall shear stress can be calculated using the formula τ = μ (du/dy), where μ is the dynamic viscosity and du/dy is the velocity gradient at the wall. Remember, higher viscosity leads to higher shear stress!
What happens when we have a rough surface?
Great point! A rough surface increases the turbulence and the wall shear stress due to enhanced friction. It’s essential to consider surface texture in engineering applications.
In summary, wall shear stress is vital in analyzing the interaction between fluids and boundaries, affecting our designs in fluid systems.
Stream Functions and Their Applications
Unlock Audio Lesson
Now let's move on to stream functions! Can anyone explain what a stream function is?
Is it a way to visualize the flow of fluid?
Exactly! Stream functions help us visualize the flow patterns. In two-dimensional, incompressible flow, if we know the stream function, we can derive the velocity components from it.
How does that relate to the velocity potential?
Another great question! The velocity potential and stream functions are related because in irrotational flows, the gradient of the velocity potential gives the velocity vector. For stream functions, the velocity components can be expressed as u = ∂ψ/∂y and v = -∂ψ/∂x.
Why is it important to differentiate between these functions?
The distinction is crucial for understanding flow characteristics. Stream functions are particularly helpful in analyzing and plotting two-dimensional flows, while velocity potentials are used in irrotational flows.
In summary, stream functions allow us to simplify fluid flow analysis, providing a clear method to visualize streamlines and compute velocities.
Application of Wall Shear Stress and Stream Functions
Unlock Audio Lesson
Let's put this all together. How do wall shear stress and stream functions apply in real-world situations?
Maybe in designing dams or bridges?
Yes! Accurate predictions of wall shear stress are essential for ensuring stability and safety in such structures. Stream functions assist in modeling the flow around these structures.
What about in airfoil design?
Absolutely! Understanding the wall shear stress and the flow patterns around airfoils helps engineers design more efficient wings that reduce drag and improve lift.
So, they are interconnected?
Exactly! Wall shear stress influences flow separation, and understanding flow through stream functions helps analyze complex flows, leading to better designs.
In summary, the interplay between wall shear stress and stream functions is crucial in various engineering applications, highlighting their significance in fluid dynamics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the concepts of wall shear stress and stream functions, providing a detailed discussion on how these concepts relate to the Navier-Stokes equations and their implications in analyzing fluid behaviors under various conditions.
Detailed
Wall Shear Stress and Stream Functions
In this section, we explore fundamental concepts in fluid mechanics, namely wall shear stress and stream functions, which play crucial roles in understanding flow dynamics in various scenarios. The discussion begins with a recap of the Navier-Stokes equations, emphasizing their derivation from the Euler equations, and how these equations relate to fluid flow characteristics, particularly the incompressible viscous flows between fixed and moving plates.
Key Concepts
Wall Shear Stress
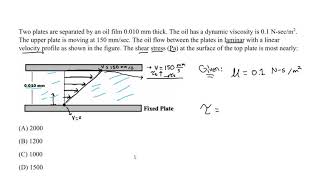
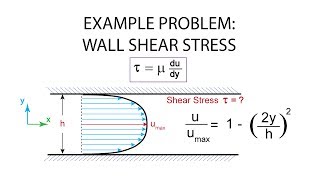
Wall shear stress is the tangential force per unit area exerted by a fluid at the boundary of a solid surface. It is pivotal in assessing frictional forces in fluid flow scenarios, impacting the design of structures like pipelines and channels.
Stream Functions
Stream functions are mathematical constructs that simplify the visualization of fluid flow, especially in two-dimensional, steady, incompressible flow. They help visualize streamlines, which denote the path followed by fluid particles. The relationship between the stream function and velocity potential aids in describing flow fields in a more intuitive manner.
Applications in Fluid Mechanics
Understanding stream functions and wall shear stress enables engineers and scientists to predict flow patterns accurately, analyze pressure distributions, and evaluate potential performance issues in fluid transport systems. The interplay between these concepts influences practical applications ranging from aerodynamics around structures to the lubrication mechanism in mechanical systems.
This section solidifies our comprehension of fluid behavior under varying dynamic conditions, reinforcing the importance of using mathematical tools like stream functions to model complex real-world scenarios effectively.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Wall Shear Stress
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In fluid mechanics, wall shear stress is an important parameter in understanding how fluids interact with surfaces. It is defined as the tangential force exerted by a fluid per unit area at a solid boundary.
Detailed Explanation
Wall shear stress (τ) arises due to the viscosity of the fluid and is calculated using the formula: τ = μ (du/dy), where μ is the dynamic viscosity of the fluid, du is the change in velocity, and dy is the distance from the wall. This means that if the fluid moves faster, the shear stress increases. Close to the wall, the fluid's velocity is affected directly by the wall's resistance.
Examples & Analogies
Imagine spreading butter on a piece of bread. As you push the knife (analogous to the fluid) across the bread (the wall), the butter near the blade moves faster than the butter further away, which remains almost still. The resistance you feel when pushing the knife through the butter is similar to wall shear stress in fluid motion.
Concept of Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Stream functions are used to describe the flow of a fluid in a two-dimensional incompressible flow field. In this context, stream functions help visualize flow patterns and are defined such that the flow velocity can be derived from it.
Detailed Explanation
In a two-dimensional flow, the velocity components (u, v) can be expressed in terms of a stream function (ψ) by using the relationships: u = ∂ψ/∂y and v = -∂ψ/∂x. This means that if you know ψ, you can derive how fast the fluid is moving in both the x and y directions. Stream functions ensure that the continuity equation is satisfied, as the divergence of velocity fields goes to zero, indicating no accumulation of fluid.
Examples & Analogies
Think of a river flowing through a valley. The stream function acts like a map that shows how the river is flowing. Different values of the stream function can represent different streamlines, like different paths the water takes. Just like on a map, where certain paths connect, stream functions show how water flows without ever crossing paths within the same streamline.
Relationship Between Stream Functions and Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The relationship between stream functions and wall shear stress plays a crucial role in characterizing fluid flows, especially in boundary layer flows.
Detailed Explanation
In boundary layer theory, the wall shear stress can be related to the velocity gradients derived from stream functions. The shear stress can be understood better by analyzing how the flow changes close to the wall, where the velocity transitions from zero (due to the no-slip condition) at the wall to higher values within the fluid. This gradient gives an indication of how much effort is needed to maintain the flow's momentum against the wall's resistance.
Examples & Analogies
Consider water flowing past a dock. At the surface of the dock, the water is nearly stationary (like the no-slip condition), but a little further out, it flows freely. The change in speed between where the water just touches the dock and where it flows quickly is similar to the velocity gradient in a stream function, affecting the shear stress felt at the dock. The steeper the change in flow, the higher the shear stress acting on the dock.
Applying These Concepts in Practical Scenarios
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In engineering applications such as pipe flow, aerodynamics, and lubrication, knowing how to calculate wall shear stress and use stream functions is essential for accurate modeling and design.
Detailed Explanation
In practical scenarios, engineers use wall shear stress and stream function concepts when designing systems that encounter fluid flow. For instance, in pipe flow situations, understanding how shear stresses work can predict how a pipe will wear over time or how to optimize the diameter for the desired flow rate. Stream functions simplify complex flow patterns into manageable equations that can be solved to predict fluid behavior in various conditions.
Examples & Analogies
Imagine designing an oil pipeline. Knowing the shear stress helps engineers estimate how much material the pipeline will need to withstand pressure and friction from the flowing oil. By visualizing the flow with stream functions, they can also determine the most efficient route that reduces wear and tear, much like choosing the best path in a hiking trail to avoid rough terrain.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Wall Shear Stress
-
Wall shear stress is the tangential force per unit area exerted by a fluid at the boundary of a solid surface. It is pivotal in assessing frictional forces in fluid flow scenarios, impacting the design of structures like pipelines and channels.
-
Stream Functions
-
Stream functions are mathematical constructs that simplify the visualization of fluid flow, especially in two-dimensional, steady, incompressible flow. They help visualize streamlines, which denote the path followed by fluid particles. The relationship between the stream function and velocity potential aids in describing flow fields in a more intuitive manner.
-
Applications in Fluid Mechanics
-
Understanding stream functions and wall shear stress enables engineers and scientists to predict flow patterns accurately, analyze pressure distributions, and evaluate potential performance issues in fluid transport systems. The interplay between these concepts influences practical applications ranging from aerodynamics around structures to the lubrication mechanism in mechanical systems.
-
This section solidifies our comprehension of fluid behavior under varying dynamic conditions, reinforcing the importance of using mathematical tools like stream functions to model complex real-world scenarios effectively.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a pipe flow scenario, the calculation of wall shear stress is crucial to design efficient piping systems that minimize energy losses.
-
Stream functions are used to visualize airflow patterns over an airplane wing, aiding in the design for optimal lift.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For fluid on a wall, stress it will stall, shear makes it crawl, making flow fall.
📖 Fascinating Stories
-
Imagine a river flowing over a rock. The water brushes against the rock, making it slippery. The force pushing sideways is the wall shear stress helping the water glide over.
🧠 Other Memory Gems
-
Remember 'V.S.W': Viscosity leads to Shear stress at the Wall.
🎯 Super Acronyms
S.F.A. for Stream Functions are Fundamental for Analyzing flows.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Wall Shear Stress
Definition:
The tangential force per unit area exerted by a fluid at the boundary of a solid surface.
-
Term: Stream Function
Definition:
A mathematical function used to represent the flow field of a fluid, which simplifies the analysis of fluid motion.
-
Term: Velocity Potential
Definition:
A scalar function from which the velocity field of a fluid flow can be derived, applicable in irrotational flow.
-
Term: Incompressible Flow
Definition:
A flow where the fluid density remains constant throughout the fluid motion.
-
Term: Turbulence
Definition:
A flow regime characterized by chaotic changes in pressure and flow velocity.