Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Velocity Potential Functions
Unlock Audio Lesson
Today, we will discuss velocity potential functions and how they can simplify fluid flow problems. Does anyone know what this function is?
Is it related to how we express the velocity fields in fluid dynamics?
Exactly! Velocity potential functions allow us to convert the vector velocity field into a scalar field, which is easier to handle mathematically. Remember, V equals the gradient of φ.
So, what conditions must be satisfied to use this method?
Great question! The main condition is that the flow must be irrotational. When vorticity is negligible, we can effectively use these potential functions.
So, if there's vorticity, we can't use this simplification?
Correct! Remember, in regions where the flow is rotational, velocity potentials cannot be applied.
So to summarize: Velocity potential functions help represent fluid flow as scalar fields, but they apply under irrotational flow conditions.
Navier-Stokes Equations Simplification
Unlock Audio Lesson
Let's shift to the Navier-Stokes equations. How do we apply simplifications when dealing with viscous flows?
Do we ignore certain terms to make the equations more manageable?
Exactly! In many cases, we can neglect gravity effects, pressure gradients, and non-axial flow, which helps us reduce the complexity of the equations.
How does that relate to fully developed flow then?
In fully developed flow, the velocity profiles do not change along the flow direction, so the equations simplify even further. This is key for solving flow between plates.
That's interesting! So once we reduce the equations, we can integrate them more easily?
Absolutely! The objective is to reach ordinary differential equations that are much easier to handle. Let's recap: we simplify the Navier-Stokes equations based on flow conditions to derive meaningful results.
Boundary Conditions and Applications
Unlock Audio Lesson
Finally, let's discuss boundary conditions when applying these concepts in practical scenarios. Why are they important?
Boundary conditions help define how the flow behaves at the edges of the system, right?
Exactly! Without proper boundary conditions, we cannot solve for aspects like shear stress or velocity profiles effectively.
Can you give an example of a boundary condition?
Sure! In flows between two plates, we often set the velocity at the fixed plate to zero while the moving plate might have a specified velocity.
So if I apply these concepts, I'll get reliable velocity distributions and shear stress information?
Right! To summarize, boundary conditions are essential for accurately applying fluid mechanics principles and calculating flow characteristics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section outlines the importance of smooth functions in fluid dynamics, particularly in the context of the Navier-Stokes equations. It details how velocity potential functions can represent flow fields, particularly in irrotational flows, and addresses the simplifications made when analyzing viscous flow between fixed and moving plates.
Detailed
Smooth Function Requirements
This section focuses on the conditions and requirements for functions to be considered smooth in fluid mechanics. This is particularly relevant when dealing with the Navier-Stokes equations and their applications to various fluid flow scenarios.
Key Points:
- Velocity Potential Functions: The section introduces velocity potential functions as a means to simplify fluid flow problems, especially in irrotational flows where the velocity field can be defined through a scalar potential function.
- When velocity V is defined as the gradient of potential function φ, it enables a reduction from three scalar components (u, v, w) to a single function, making problem-solving more efficient.
- Irrotational Flow Conditions: It emphasizes that the use of velocity potential functions is valid only under specific conditions, notably irrotational flow where vorticity is negligible.
- Navier-Stokes Equations and Simplifications: The section discusses how simplifying assumptions can be applied to the Navier-Stokes equations to find solutions for viscous flows, such as those occurring between fixed and moving plates or in pipe flows.
- Boundary Conditions and Fully Developed Flow: Attention is given to boundary conditions and new ways to analyze flow patterns, particularly the transition from potential functions to shear stress and pressure gradients.
Ultimately, the section underscores the significance of smooth functions in deriving mathematical models for fluid dynamics and provides foundational insights for interpreting complex fluid behavior.
Youtube Videos
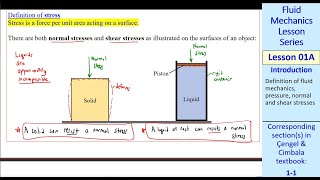
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Velocity Potentials
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let me go through the basic things what we discussed that basically we are going to introduce velocity potentials okay. I will discuss more details. very interesting things, generations of rotationality.
Detailed Explanation
This chunk introduces the concept of velocity potentials, which are mathematical functions used to simplify the analysis of fluid flows. The instructor aims to explain how these potentials can help describe movement in fluids more easily, especially in relation to rotational flow dynamics.
Examples & Analogies
Think of it like using a map (velocity potential) to navigate through a city (fluid movement). The map simplifies the landscape, helping you to understand how to get from point A to point B without getting lost in the details.
Definition of Velocity Potential Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The velocity potentials is similar to analogous to the electric field potentials and the current.
Detailed Explanation
Velocity potential functions represent the velocity field in a fluid flow. They're defined as scalar functions from which the velocity vector can be derived by taking spatial derivatives. Specifically, if phi is the velocity potential, the components of velocity can be expressed as the gradient of phi.
Examples & Analogies
Imagine a mountain landscape. The height at each point can be thought of as potential energy. Just like how water flows down from higher elevations (potential), fluids move faster in regions of higher 'pressure' or velocity potential.
Conditions for Using Velocity Potential Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus if I define it the velocity is a gradient of phi, phi is a velocity potential function at which condition thus this is what justified it was.
Detailed Explanation
For the velocity potential functions to be valid, the flow must be irrotational, meaning there is no rotation of fluid elements. In such a flow, the divergence of the curl (cross-product) of the velocity field is zero. The necessity of this condition ensures that the mathematical model accurately reflects fluid dynamics.
Examples & Analogies
Think of a perfectly still pond. If you gently toss a stone, the ripples that form are like the velocity field. If the water were to rotate in spirals instead of moving outward, the conditions for the velocity potential function wouldn't hold.
Orthogonality of Streamlines and Potential Lines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The only things is difference here that the stream functions exist for two-dimensional cases okay.
Detailed Explanation
This chunk examines the relationship between streamlines (paths followed by fluid particles) and equipotential lines (lines of constant velocity potential). Under certain conditions, these two types of lines are orthogonal to each other, meaning they intersect at right angles, showcasing important relationships in fluid flow.
Examples & Analogies
Imagine walking along the lines of a grid in a city (streamlines) while being aware of the location of scenic spots (equipotential lines). The places you consider attractive to visit are always at right angles to your path — navigating these lines gives you the most interesting view of the city and how it functions.
Understanding Rotational vs. Irrotational Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The same concept is here instead of the laws of motions here we talk about the rotations that means if the flow field is irrotational okay.
Detailed Explanation
The flow field can be either irrotational or rotational based on the presence of external stressors. For example, if a liquid flows smoothly without any spins or rotations, it is irrotational. However, introducing obstacles can create rotational effects, therefore altering the fluid dynamics significantly. Understanding the difference is key to predicting fluid behavior accurately.
Examples & Analogies
Think of a smooth stream (irrotational) and a whirlpool (rotational). In the stream, every drop of water flows linearly, while in the whirlpool, water rotates around a central point. This highlights how motion changing from one state to another can greatly affect the overall flow characteristics.
Using Velocity Potentials in Calculations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But the conditions what we have the flow should be the irrotational flow field or the regions where the rotational activities merely or negligible components okay.
Detailed Explanation
This chunk reinforces the importance of identifying the correct conditions under which velocity potentials can be applied. It emphasizes that they are only appropriate in irrotational flow fields. If the flow deviates from this condition, then calculations, especially those involving potential functions, could yield inaccurate results.
Examples & Analogies
Consider a person trying to draw a straight line on a wrinkled piece of paper versus on a perfectly flat sheet. It's much easier and more accurate to draw on the flat paper (irrotational conditions) than on the wrinkled one (rotational conditions), which causes the lines to curve unexpectedly.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Velocity Potential Function: A tool to reduce complex vector fields into manageable scalar expressions.
-
Irrotational Flow: A condition necessary for using velocity potential functions; flow without vorticity.
-
Navier-Stokes Equations: The primary equations governing fluid motion, requiring careful simplifications for solvable forms.
-
Continuity Equation: A critical equation ensuring mass conservation within fluid flows.
-
Boundary Conditions: Vital constraints needed to obtain meaningful solutions in fluid mechanics problems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A fluid flow between two parallel plates where one is moving can be analyzed using the velocity potential function.
-
Finding the pressure distribution for a simple flow problem can involve applying the Navier-Stokes equations with simplified terms.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When flows are smooth without much whir, use potential functions to infer.
📖 Fascinating Stories
-
Imagine a calm river where the water flows smoothly, showing no signs of turbulence—a perfect scenario for applying velocity potentials.
🧠 Other Memory Gems
-
Remember the acronym SIP: Simplify, Identify, and Apply when working with Navier-Stokes equations.
🎯 Super Acronyms
VIP for velocity potential—Velocity is the Gradient of the Potential!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Velocity Potential Function
Definition:
A scalar function whose gradient represents the velocity field in fluid dynamics.
-
Term: Irrotational Flow
Definition:
A flow condition where the fluid particles do not exhibit vorticity.
-
Term: NavierStokes Equations
Definition:
A set of nonlinear partial differential equations that describe the motion of viscous fluid substances.
-
Term: Continuity Equation
Definition:
An equation representing the principle of conservation of mass in fluid dynamics.
-
Term: Boundary Condition
Definition:
Constraints that define the behavior of fluid at the boundaries of the domain of interest.