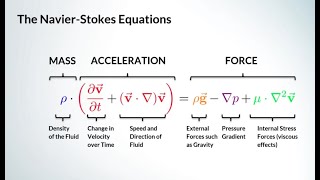
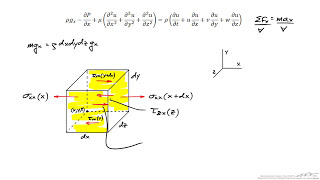
Continuity and Navier-Stokes Equations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Mechanics Concepts
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning, everyone! Today we'll explore the continuity equation and the Navier-Stokes equations. To start, can anyone tell me what the continuity equation represents?

Isn’t it about mass conservation in fluids?

Exactly! The continuity equation helps us understand how mass moves through a fluid. It's represented mathematically as the divergence of velocity being equal to zero in incompressible flows. Why do you think this is important?

Because it ensures that fluid flow is steady without any mass loss.

Right! This leads us to the Navier-Stokes equations, which we use to describe fluid motion. Remember, a helpful acronym for these concepts is 'FLOWS' — 'Fluid Laws of System'.

How do these equations interact with each other?

Great question! The Navier-Stokes equations relate velocity and pressure fields, effectively linking the continuity and momentum equations to model real-world fluid dynamics.

So they work together in a system to predict fluid behavior?

Exactly! Now, let’s summarize what we discussed: The continuity equation is crucial for mass conservation, and the Navier-Stokes equations allow us to analyze fluid flow under various conditions.
Velocity Potential Functions and Irrotational Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Continuing from our last session, let’s dive into velocity potential functions. Who can explain what they are?

Velocity potential functions help simplify calculations in fluid flow by reducing multiple velocity components into one scalar function.

Perfect! And when can we use these functions, specifically regarding flow behavior?

They can only be used under irrotational flow conditions.

That’s right! The concept of irrotational flow, where the vorticity is negligible, simplifies our calculations significantly. An easy way to remember this is through the term 'VAPOR' — 'Velocity And Potential of Irrotational Flow.'

How do we represent velocity using this function?

We represent velocity as the gradient of the potential function Phi: V = ∇Phi. This means we can express the velocity components as partial derivatives of phi regarding space coordinates.

Can you remind us what conditions define irrotational flow?

Certainly! For flow to be irrotational, we need the curl of velocity to equal zero. To recap: Velocity potential functions significantly aid in our calculations, but we can only use them in irrotational flow.
Application of Navier-Stokes Equations in Practical Scenarios
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's talk about applying Navier-Stokes equations in practical scenarios. Can anyone give me an example?

How about flow past tall buildings?

Great example! The flow around tall structures makes us think about shear stress and pressure gradients. We often use these equations when analyzing airflow to account for vorticity near the structure.

So how do we deal with the complexities of turbulent flow in these situations?

Good point! Turbulent flow complicates matters, and in such cases, we often use computational methods and approximations to simplify our solutions.

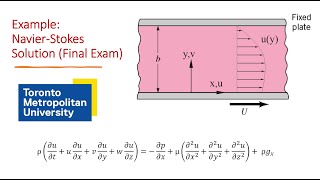
What about when flow is between two plates? How do we analyze that?

Excellent! For flow between two plates, we start by identifying pressure gradients and using them along with Navier-Stokes to solve for velocity distributions across the gap. Remember the linearization we discussed earlier.

So, each flow scenario requires us to adapt our methods?

Exactly! Recap: We've examined how Navier-Stokes applies to flow around tall structures and between plates, adapting methods based on each situation.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section elaborates on how the continuity equation and Navier-Stokes equations are foundational in understanding fluid flow. It covers various concepts such as velocity potential functions, irrotational flow, and examples of incompressible viscous flow between moving plates, demonstrating the application of these equations in real life.
Detailed
In fluid mechanics, the continuity equation and Navier-Stokes equations play crucial roles in modeling fluid behavior. The continuity equation represents mass conservation in the flow, emphasizing how velocity and pressure are interrelated in incompressible flows. The section delves into deriving the continuity equation, applying Navier-Stokes equations to various scenarios such as the flow past tall buildings, and using velocity potential functions to simplify calculations. Specifically, it discusses irrotational flow conditions where the vorticity is negligible, allowing for the definition of velocity in terms of a single scalar function, the velocity potential. The significance of flow characteristics, like boundary layers and shear stress, is also highlighted through practical examples, emphasizing the necessity of examining fluid behavior in engineering applications.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Navier-Stokes Equations
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So basically let us start with Navier-Stokes equations which is long back about 200 years back. So the equations what we derive in last two classes we will go more detail about that.
Detailed Explanation
The Navier-Stokes equations describe the motion of fluid substances. These equations have been developed over the past 200 years and summarize the principles of fluid dynamics, including how fluids flow and behave under various conditions. In fluid mechanics, these equations are crucial for predicting how fluid will move in different scenarios, such as air flowing over an aircraft or water flowing through a pipe.
Examples & Analogies
Imagine a person swimming through water. The movements of the person's body create waves and currents in the water. The Navier-Stokes equations help us understand how those waves and currents change based on the person's movements and the water's properties.
Euler Equations and Their Validity
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When I talk about Euler equations you can understand it. It is for incompressibles and non-viscous or fixed or less flow. So if you consider flow past a tall building.
Detailed Explanation
Euler equations are a form of the Navier-Stokes equations but are simplified by assuming the fluid is incompressible and non-viscous. These equations can be used to model flows where viscosity has a negligible effect, such as in large-scale phenomena. For example, when analyzing the airflow around tall buildings, the flow outside the immediate vicinity of the building can be approximated using Euler's equations, as viscosity's influence diminishes at larger distances from the building.
Examples & Analogies
Think of a smooth river flowing around a rock. The water flows around the rock without much turbulence in the broader flow, making it possible to use simplified equations, like Euler’s, to describe the water movement without considering every tiny eddy and whirlpool.
Velocity Potential Functions
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Instead of looking at 3 scalar velocity components why we cannot write it with a simple a scalar function that is what is the velocity potential function.
Detailed Explanation
In fluid dynamics, using velocity potential functions allows for a simplified approach to dealing with flow fields. Rather than handling three different velocity components (u, v, w), we can describe the flow using a single scalar function, known as the velocity potential function (φ). This function's gradients in different directions give us the velocity components, thus reducing the complexity of our calculations significantly.
Examples & Analogies
Imagine trying to navigate a large, crowded room. If you focus on every person's movement (u, v, and w), it can be overwhelming. Instead, if you have a general idea of how people will flow based on the entrances and exits (the velocity potential function), you can easily predict traffic patterns without tracking every individual.
Conditions for Velocity Potential Functions
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If I define the velocity as the gradient of phi, phi is the velocity potential functions, the condition is that it should be irrotational flow.
Detailed Explanation
The use of velocity potential functions requires specific conditions. One key condition is that the flow must be irrotational, which means there is no rotation or vorticity in the fluid. When the flow is irrotational, it simplifies calculations, allowing the velocity fields to be expressed as the gradient of a single scalar function (the velocity potential). This means that the flow behaves in a predictable manner without swirling eddies or chaotic turbulence.
Examples & Analogies
Think of a calm pond where you drop a rock. The ripples that form move outward in circular patterns without causing any spinning water. This is similar to irrotational flow in a fluid where the potential function can accurately predict the flow’s behavior.
Relation Between Streamlines and Potential Lines
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The streamlines and the potential lines they will have a orthogonality to each other.
Detailed Explanation
In fluid dynamics, streamlines represent the paths that fluid particles follow, while potential lines are connected to the velocity potential function. One important characteristic of these two types of lines is that they are orthogonal or perpendicular to each other at the points where they intersect. This orthogonality indicates that the direction of fluid flow (streamlines) is at a right angle to the direction of potential gradient, which portrays how velocity is changing in space.
Examples & Analogies
Consider a playground slide and a path leading up to it. The path (potential line) intersects the slide (streamline) at a right angle, indicating how one leads to the other. As you walk up, you can glance down the slide; however, your direction of travel is always perpendicular to the slide’s surface.
Key Concepts
-
Continuity Equation: A basic principle in fluid dynamics representing mass conservation in a flow.
-
Navier-Stokes Equations: Core equations for understanding the motion of viscous fluids.
-
Irrotational Flow: Special flow conditions in which the vorticity is zero, simplifying calculations.
-
Velocity Potential Functions: Tools that reduce the complexity of fluid flow calculations in irrotational flow.
Examples & Applications
Example of a flow past tall buildings where the continuity equation and Navier-Stokes equations are applied.
Flow between two plates where pressure gradient induces velocity, demonstrating shear stress.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Continuity’s plain as day, fluids flow, but don’t stray!
Stories
Imagine a river flowing smoothly without any ripples; this symbolizes continuity and irrotational flow.
Memory Tools
FLOWS: 'Fluid Laws of System' helps remember principles governing fluid flow.
Acronyms
VAPOR
'Velocity And Potential of Irrotational Flow' summarizes the key aspects of potential functions.
Flash Cards
Glossary
- Continuity Equation
An equation that represents the conservation of mass in a fluid flow.
- NavierStokes Equations
Fundamental equations in fluid mechanics that describe the motion of viscous fluid substances.
- Irrotational Flow
Flow where the vorticity is negligible, allowing for the use of velocity potential functions.
- Velocity Potential Function
A scalar function from which the velocity at any point in an irrotational flow can be derived.
- Vorticity
A measure of the local rotation of a fluid element in the flow field.
Reference links
Supplementary resources to enhance your learning experience.
