Enrol to start learning
Reading is open to everyone. Enrolling is free, and it is what unlocks the audio lessons, practice tests and progress tracking.
6.7.1. Genetic Algorithms
Interactive Audio Lesson
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Today, we will dive into genetic algorithms, also known as GAs. They are inspired by the process of natural evolution. Can anyone tell me how this concept might apply to solving complex problems?
Are they like how we pick the best plants or animals to breed?
Exactly! Just like we breed stronger plants or animals, GAs breed better solutions. What do you think happens after selecting the best individuals?
Don't we combine features of the best ones?
Right! We use genetic operators like crossover to combine them. This is essential as it helps keep diversity within the solutions. Does anyone know why diversity is essential?
To avoid getting stuck in local optima?
Exactly! Keeping diversity prevents premature convergence. In summary, GAs take a population of solutions, evaluate them, select the best, and breed new generations until we find a satisfactory solution.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Now let’s talk about how GAs work. Who can outline the primary steps in the genetic algorithm process?
I think they start with generating a random population of solutions.
Correct! After generating solutions, we evaluate each solution based on a fitness function. What do you think a fitness function does?
It measures how good a solution is.
Exactly! Once we have fitness scores, we can select the best solutions for mating. This leads to crossover and mutation phases. Can anyone explain what crossover and mutation entail?
Crossover combines aspects of two parent solutions, while mutation makes random changes.
Spot on! These processes create new individuals which are then assessed for fitness again. Each generation improves over time, helping us inch closer to an optimal solution.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free accountLet's pivot to where genetic algorithms fit in VLSI design. Can anyone think of specific applications for GAs?
They could be used for placing components on a chip or routing.
Absolutely! GAs help navigate the complex constraints involved in these problems. How do you think they compare to traditional methods?
Maybe they are better at avoiding getting stuck in poor solutions?
Exactly! They excel at traversing large solution spaces and finding better solutions over successive generations. Can anyone summarize why GAs are beneficial for VLSI design?
They evolve solutions over time and can handle complex constraints effectively.
Great summary! Genetic algorithms are indeed powerful tools for solving optimization issues in VLSI design.
Overview
Short Summary
Genetic algorithms are heuristic optimization techniques inspired by natural selection, used in complex optimization problems in VLSI design.
Medium Summary
This section discusses genetic algorithms as advanced optimization techniques in VLSI design, explaining their functioning, advantages, and how they evolve solutions through generations, making them suitable for handling complex design challenges.
Detailed Summary
Genetic Algorithms
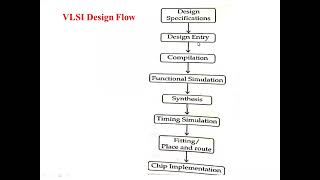
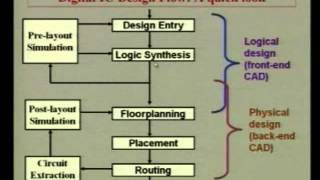
Genetic algorithms (GAs) are a class of heuristic optimization algorithms that mimic the process of natural selection to solve complex optimization problems, particularly in fields such as VLSI design. They represent potential solutions to a problem as individuals in a population and evolve these solutions over generations. In this section, we will break down the essential components and functioning of genetic algorithms, their significance in VLSI design, and their advantages over traditional optimization methods.
Key Points:
- Heuristic Optimization: Genetic algorithms are particularly useful when traditional optimization methods are inefficient or inapplicable due to problem complexity.
- Population-Based Approach: GAs work with a population of solutions, allowing them to explore multiple paths simultaneously.
- Natural Selection: Solutions are evaluated, and the best-performing candidates are selected for reproduction.
- Genetic Operators: Key processes such as crossover (recombination of two individuals) and mutation (random alterations) create diversity in the population, preventing premature convergence to local optima.
- Generational Evolution: The algorithm iteratively improves the population by selecting, crossing over, and mutating solutions across generations until a satisfactory solution emerges.
- Applications in VLSI: GAs are applied in various stages of VLSI design ranging from placement to routing, where traditional methods may falter.
Genetic algorithms play a critical role as advanced optimization techniques, complementing other strategies like simulated annealing and particle swarm optimization to tackle the intricacies associated with modern VLSI designs.
Reference YouTube Videos
Audio Book
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountGenetic algorithms are heuristic optimization algorithms that mimic the process of natural selection.
Detailed Explanation
Genetic algorithms (GAs) are a type of optimization algorithm inspired by the principles of natural evolution. They function by evolving a set of potential solutions over several generations. Each solution is analogous to an organism in nature, competing for resources. Just like in nature, where the fittest organisms survive and reproduce, in GAs, the most effective solutions are selected to create new solutions. Over multiple generations, this process aims to improve the overall quality of the solutions and approach an optimal solution.
Examples & Analogies
Imagine a farmer selecting the best plants from the harvest season. Each year, the farmer sows seeds from the healthiest, most productive plants, which results in a progressively stronger crop over time. Similarly, genetic algorithms continuously refine their solutions by picking the best 'plants' (solutions), leading to better outcomes with each iteration.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountGenetic algorithms are used for complex optimization problems where traditional methods are not efficient.
Detailed Explanation
GAs are particularly useful in scenarios where the search space is vast and convoluted, making it difficult for traditional optimization methods (like gradient descent) to find a solution quickly. For instance, in complex design problems where there are multiple conflicting objectives or constraints, GAs can help in simultaneously optimizing various aspects. They efficiently explore the solution space by maintaining a diverse set of potential solutions, thereby avoiding getting stuck in local optima.
Examples & Analogies
Think of a treasure hunt in a massive maze. While traditional methods may allow you to explore paths gradually and might miss the treasure entirely, a genetic algorithm would swiftly guide a group of 'explorers' in different directions, allowing them to find multiple paths at once. After assessing which paths yield better results, they focus their energies on the most promising routes, ensuring they adapt and improve their chances of discovering the treasure.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountThey evolve a population of solutions over several generations to find near-optimal solutions.
Detailed Explanation
In genetic algorithms, the evolution process involves several key steps: selection, crossover, and mutation. Selection involves choosing the best solutions from the current population based on a fitness function, which measures how good a solution is for a given problem. Crossover combines pairs of solutions to create new offspring that inherit characteristics from both parents. Mutation introduces small random changes to some solutions, which helps maintain diversity and prevents premature convergence on suboptimal solutions. These steps are repeated across many generations, each time refining the solutions until an acceptable near-optimal solution is found.
Examples & Analogies
Imagine a cooking competition where chefs create new dishes by combining ingredients. The judges pick the best dishes (selection), and the chefs then mix components from top dishes to create new versions (crossover). Occasionally, a chef might experiment and add an unexpected spice (mutation) to keep things exciting. Over several rounds of cooking and tasting, the chefs learn and adapt to produce the ultimate dish that pleases the judges.
--
Key Concepts
Core takeaways and short definitions to help you quickly recall the key ideas from this section.
Heuristic Optimization: A method that seeks satisfactory solutions for complex problems when traditional methods are not efficient.
Population-Based Approach: Solutions are treated as individuals in a population, allowing exploration of multiple possibilities.
Crossover and Mutation: Key operators used to create new solutions, ensuring diversity and exploration in the search space.
Iterative Improvement: The process of evolving solutions across generations to approach an optimal solution.
Examples
Step-by-step examples to apply the section's ideas and test your understanding.
A genetic algorithm might be used to optimize the placement of components on a VLSI chip, combining placements that minimize wirelength.
In routing, genetic algorithms can find efficient paths for interconnections, balancing power consumption and area.
Memory Aids
Interactive tools to help you remember key concepts
Stories
Memory Tools
Flash Cards
Glossary
Genetic Algorithm
A heuristic optimization algorithm that mimics the process of natural selection to evolve solutions to problems.
Population
A set of potential solutions to the optimization problem.
Fitness Function
A measure used to evaluate how well a solution solves the problem at hand.
Crossover
A genetic operator that combines parts of two parent solutions to create offspring solutions.
Mutation
A genetic operator that introduces random changes to a solution to maintain diversity in the population.