Finding Appropriate Control Volumes
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Control Volumes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to learn about control volumes in fluid mechanics. Can anyone tell me why they are critical when analyzing flow systems?

They help us to apply the conservation laws effectively?

Exactly! Control volumes help us ensure that we apply mass, momentum, and energy conservation principles correctly. Remember, our goal is to select volumes where the flow conditions are predictable.

What should we look for in an ideal control volume?

Great question! We should aim for areas with parallel streamlines since that minimizes complications from turbulence. Can anyone visualize what turbulence might do?

It causes vortex formations, right? Which can lead to inaccurate calculations.

Precisely! Turbulent flow introduces complexities we want to avoid when analyzing as they lead to energy losses. Always remember this: 'Turbulence ≠ Predictable Flow'. Let's summarize this part: Control volumes should ideally have parallel streamlines to ensure accurate, predictable fluid analyses.
Types of Flow Losses
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s talk about flow losses. Who can tell me the difference between major and minor losses in piping systems?

Major losses are from friction, while minor losses come from fittings and bends, right?

Good! Major losses occur due to friction in the pipe surfaces, while minor losses are from changes in how the fluid moves, like bends and fittings. Can anyone give me an example of a minor loss?

An elbow fitting in a pipe could cause a minor loss.

"Correct! To quantify these losses, we experimentally measure pressure differences across fittings. Remember the equation we'll likely use for energy losses is:
Experimentation Techniques
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Moving forward, how do we actually measure the energy losses we've discussed?

Do we use manometers to gauge pressure differences?

Absolutely right! Using manometers helps us measure pressure differences which we can use to calculate losses using Bernoulli's equation. Keep in mind, knowing the velocity of flow is equally critical. Can anyone tell me what influences velocity in pipes?

The diameter of the pipes would influence the velocity, right?

"Yes, exactly! A smaller diameter increases velocity, leading to higher kinetic energy, which can also influence losses. Always visualize this equation:
Practical Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Lastly, let’s connect these concepts to real-world applications. Why is understanding control volumes crucial in designing plumbing systems?

Because we need to plan for energy efficiency while ensuring sufficient flow to different outlets.

Exactly! For instance, in a municipal water supply system, understanding losses can dictate the size of pumps needed and the layout of pipes. If we overlook losses, we can end up with inadequate supply in peak demand times. So it's essential that—what do we remember during our analysis?

Control volumes must be selected carefully, especially avoiding turbulent flow areas!

Wonderful! Remember that analyzing control volumes thoroughly can lead to significant improvements in system designs. To sum up, control volumes help optimize municipal systems by minimizing energy losses.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The selection of control volumes is crucial in analyzing fluid flows and energy losses in pipe systems. Understanding turbulence, characterizing fluid types, and quantifying losses through experimentation are necessary to design efficient supply systems.
Detailed
Finding Appropriate Control Volumes
In fluid mechanics, particularly when studying viscous flows through pipes, selecting an appropriate control volume is essential for accurate analysis and calculation of flow behaviors. This section emphasizes the concept that control volumes should be chosen based on where flow dynamics are more predictable, such as parallel streamlines, to avoid inaccurate assumptions and calculations.
Key Points
- Definition of Control Volume: A control volume is a designated space in the flow field used for applying the conservation laws, such as mass conservation, energy conservation, and momentum conservation.
- Significance of Streamlines: Streamlines must be parallel within the control volume for the application of Bernoulli's equation. This aids in simplifying the complex interactions within turbulent flows and helps avoid regions of vortex formation, where flow behaviors are unpredictable.
- Understanding Energy Losses: The section discusses both major and minor losses in fluid flows. Major losses are primarily due to friction while minor losses arise from fittings, bends, and changes in pipe diameter. The aim is to minimize these losses to improve system efficiency.
- Application Examples: Students are presented with examples demonstrating how different pipe fittings and configurations affect energy losses, particularly highlighting the effects of turbulence and flow transitions.
- Experimentation: Practical methods to measure pressure differences across pipe systems are discussed, as well as using experimental data to quantify losses accurately. Different experimental setups in educational labs can help solidify these concepts practically.
In summary, understanding how to select an appropriate control volume is central to fluid mechanics. It ensures that engineers can design and analyze water supply systems efficiently while minimizing energy loss.
Youtube Videos

![System Approach and Control Volume Approach [Fluid Mechanics]](https://img.youtube.com/vi/quK9rvsZTPA/mqdefault.jpg)






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Control Volumes
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
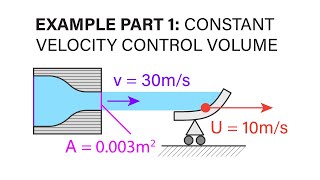
To apply energy equations like Bernoulli’s, you should take a streamline. Along the streamline, you should apply Bernoulli’s. The most appropriate streamline is this ones, you take it. Because this is a horizontal streamlines, so we can just know the pressure and velocity, pressure and the velocity and modify the Bernoulli’s equations, apply over this ones.
Detailed Explanation
This chunk emphasizes the importance of selecting the correct control volume when analyzing fluid flow. Bernoulli’s equation can only be accurately applied along a streamline, which is a path in the fluid where the flow is steady. Choosing a horizontal streamline allows for proper measurements of pressure and velocity, essential for calculations. The right streamline selection ensures that we capture the fluid behavior accurately across various flow scenarios.
Examples & Analogies
Imagine you are skating on a smooth ice rink. The ice surface is like a streamline for the flow of water. When you skate straight (along the streamline), you can maintain speed and balance (similar to pressure and velocity), but if you suddenly veer off into rough or uneven areas (like choosing an improper control volume), it becomes difficult to maintain your momentum and balance.
Choosing the Correct Control Volume
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Similar way, if I am to apply the linear momentum equations or other mass of conservations, I should consider the control volume is much bigger than affected area so that I can get it, this effect should not be there. So I can use this control volume to apply the mass conservation equations or linear momentum. Exactly same way I can use this control volume still up to this spot, apply it.
Detailed Explanation
When applying linear momentum or mass conservation equations, it is crucial to choose a control volume that encompasses a larger area than the region impacted by the flow. This approach minimizes the effects from boundary conditions, leading to a more straightforward analysis of the fluid behavior. By ensuring that the control volume is adequately sized, we can accurately evaluate the forces and changes occurring within that volume.
Examples & Analogies
Think of pouring a cup of water from a pitcher. If you aim to pour accurately, you need to ensure the cup is large enough to catch the entire stream of water without spilling. A small cup (like a poorly chosen control volume) might let some water escape, making it difficult to assess how much water was actually poured.
Avoiding Complex Streamlines
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Please do not take the control volume like this, which is totally wrong. Because you do not know it this zone what is happened it. So when you take the appropriate control volume we should take it. That means you should look it the control volume, where the streamlines are the parallel, streamlines are parallel.
Detailed Explanation
This section warns against choosing control volumes that contain complex streamlines, which can confuse the analysis. When streamlines are not parallel, it implies that there are changes in fluid speed or direction, complicating the evaluation of forces within the volume. To simplify calculations and ensure accuracy, control volumes should ideally exhibit parallel streamlines.
Examples & Analogies
Consider a river with a meandering path. If you wanted to measure the water flow, you'd ideally choose a wide section where the current flows straight (parallel streamlines). Attempting to measure in a sharp bend (complex streamlines) would give inaccurate results due to swirling and turbulence.
The Importance of Visualization
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So you try to avoid to draw the outward streamlines, find out the reasons where there are not supposed to have the streamlines having any curvatures, the more or less the parallels. Like this case I draw the streamlines all will be the parallel by the time we reach it here. These regions I can consider this part and this part anyway, it is not a difficult for us, because there is no flow boundary conditions.
Detailed Explanation
Visualizing the flow is essential for correctly determining control volumes. By avoiding outward streamlines and drawing parallel lines, we can clearly identify regions suitable for analysis. This allows for a better grasp of flow behavior and ensures that the selected areas do not have curvatures that could affect measurements.
Examples & Analogies
Imagine designing a race track. If you lay out straight lines (representing parallel streamlines), it's easier to predict where the cars will go and how fast they'll travel. If you introduce curves or bends (curved streamlines), it complicates matters drastically since cars may slow down or crash, just like how complex streamlines complicate fluid behavior.
Key Concepts
-
Control Volume: A fluid space used for applying conservation laws.
-
Energy Loss: Loss of mechanical energy in fluid flow due to friction and turbulence.
-
Parallel Streamlines: Ideal scenarios in control volumes where flow remains predictable.
Examples & Applications
In a water supply system, using a control volume around a pump helps to analyze energy losses and pumping requirements effectively.
Considering a bend in a piping system, engineers should analyze flow patterns to reduce energy losses by minimizing turbulence.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Control volumes must be neat, Parallel flow is our treat, Avoid the chaos, keep it clear, Energy losses we must steer.
Stories
Imagine a pipe system as a river flowing through a valley. If the river follows a straight path, the water flows smoothly. If it hits turns and rocks, it splashes about, indicating turbulence and lost energy. Hence, straight paths represent optimal control volumes in this analogy.
Memory Tools
P.E.T. (Parallel flow, Energy loss, Turbulence) for easy recall of critical concepts in flow analysis.
Acronyms
C.A.P. (Control volume, Analysis, Pressure) emphasizes the main aspects of fluid analysis.
Flash Cards
Glossary
- Control Volume
A designated space used in fluid mechanics to apply conservation principles for mass, momentum, and energy.
- Streamline
A line that represents the flow of fluid; all points along the streamline have the same velocity.
- Turbulence
Irregular, chaotic flow patterns in a fluid that complicate analyses and lead to energy losses.
- Major Losses
Energy losses due to friction in the fluid as it flows through a pipe.
- Minor Losses
Energy losses resulting from fittings, bends, and other changes in pipe geometry.
- Hydraulic Gradient Line
A line in a flow system that shows the total energy head available to the fluid at various points.
Reference links
Supplementary resources to enhance your learning experience.
