Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Turbulent Flow
Unlock Audio Lesson
Today we'll explore the fascinating world of fluid mechanics, specifically turbulent flow. Can anyone share what you think turbulent flow is?
Isn't it when fluid moves chaotically with lots of mixing and turbulence?
Exactly! Turbulent flow is characterized by chaotic changes in pressure and flow velocity. It's quite different from laminar flow, where fluid moves in parallel layers.
How do we actually measure whether the flow is turbulent or not?
Great question! We use the Reynolds number to classify the flow. It's a dimensionless quantity that compares inertial forces to viscous forces in the fluid.
What are the critical values for the Reynolds number again?
Good memory! For pipe flow, if Re is less than 2300, we have laminar flow; above 4000, we call it turbulent; and the range in between indicates transitional flow.
To summarize: turbulent flow is chaotic, while laminar flow is smooth. The Reynolds number is crucial in identifying the type of flow.
Understanding the Reynolds Number
Unlock Audio Lesson
Now, let's discuss how to calculate the Reynolds number. What do you think are the factors involved in this calculation?
I remember hearing about density and viscosity!
Exactly! We calculate it using the formula: Re = (ρvD)/μ. Here, ρ is the fluid density, v is the velocity, D is the diameter, and μ is the dynamic viscosity.
How does each factor influence the flow?
Great inquiry! Higher velocity or larger diameter increases Re, indicating a higher possibility of turbulent flow, while higher viscosity decreases Re, favoring laminar flow.
In recap: Reynolds number is pivotal in determining the nature of the flow, and we analyze its components to understand flow behavior.
Practical Applications of Turbulent Flow
Unlock Audio Lesson
Understanding turbulent flow isn't just theoretical; it has practical implications. How do you think this knowledge helps engineers?
Maybe in designing pipes and determining how much energy loss occurs?
Absolutely! Engineers must account for energy losses due to turbulence in pipelines. This requires careful design to minimize costly inefficiencies.
Are there tools to assist in designing these systems?
Yes! Tools like computational fluid dynamics (CFD) software help model these flows and predict behaviors effectively.
In summary, knowing about turbulent flow and Reynolds number sets the stage for designing efficient fluid transport systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains the transition between laminar and turbulent flow, defined by the Reynolds number, and discusses how turbulence is quantified. It highlights key thresholds for Reynolds numbers and their implications on fluid mechanics, particularly in pipe flow applications.
Detailed
Turbulent Flow and Reynolds Number
This section focuses on the fundamental concepts of turbulent flow in fluid mechanics and the role of the Reynolds number in determining flow regimes. Turbulent flow is a complex flow pattern characterized by chaotic and irregular motions of fluid particles. The Reynolds number is a dimensionless quantity that provides a critical differentiator between laminar and turbulent flow based on the balance between inertial and viscous forces in the fluid.
- Definition of Reynolds Number: The Reynolds number (Re) is defined mathematically as the ratio of inertial forces to viscous forces. It is calculated using the formula:
\[ Re = \frac{\rho v D}{\mu} \]
where:
- \( \rho \) = fluid density,
- \( v \) = fluid velocity,
- \( D \) = characteristic length (typically diameter for pipe flow),
- \( \mu \) = dynamic viscosity of the fluid.
- Laminar vs. Turbulent Flow: The threshold values of Reynolds number are significant in classifying flow when:
- Re < 2300: Flow is considered laminar, where fluid particles move in smooth paths or layers.
- Re > 4000: Flow is considered turbulent, featuring chaotic fluid motion with eddies and vortices.
- 2300 < Re < 4000: Transitional flow, where flow characteristics may fluctuate between laminar and turbulent.
Understanding these flow regimes is crucial in applications, such as designing pipe systems to manage energy losses effectively and ensure efficient fluid transportation.
Youtube Videos
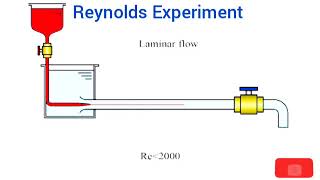
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Turbulent Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Again I am repeating these slides to just to energize to you that when you have the pipe flow, most of the times we have the turbulent flow okay.
Detailed Explanation
In most pipe flow situations, the flow is turbulent. Turbulent flow is characterized by chaotic and irregular fluid motion. This implies that the fluid particles move in a random pattern, which can lead to increased mixing and energy loss compared to laminar flow, where fluid moves in parallel layers and is more orderly.
Examples & Analogies
Think about a river. In certain areas, the water flows smoothly in layers (laminar flow), while in other areas, it swirls and churns (turbulent flow). The churning water allows for better mixing of nutrients and sediment, but it also loses energy as turbulence increases.
Reynolds Number Explained
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When you talk about the turbulence, do not look at the figures like these type of vortex phenomena and all. Always we quantify the turbulence with respect to Reynolds numbers.
Detailed Explanation
The Reynolds number (Re) is a dimensionless quantity used to predict the flow regime in fluid mechanics. It is calculated as the ratio of inertia forces to viscous forces within the fluid. A low Reynolds number (typically less than 2300) indicates laminar flow, while a high Reynolds number (above 4000) indicates turbulent flow. Values between 2300 and 4000 represent a transitional phase where both flow patterns can coexist.
Examples & Analogies
Imagine riding a bicycle. If you're pedaling slowly on smooth terrain, you move in a straight line (laminar flow). However, if you speed up and hit a bumpy road, you're more likely to wobble and zigzag (turbulent flow). The transition from a smooth bike ride to a unsteady one is akin to the transition from laminar to turbulent flow as the Reynolds number increases.
Threshold Values of Reynolds Number
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If it is a Reynolds number less than 2300 the flow is laminar. If Reynolds numbers greater than 4000 the flow is turbulent, okay?
Detailed Explanation
The determination of whether the flow is laminar or turbulent based on Reynolds number thresholds is crucial in fluid mechanics. If the Reynolds number is less than 2300, the flow remains steady and organized (laminar flow), while values above 4000 signify a chaotic and unpredictable flow pattern (turbulent flow). The range between these two thresholds is where the flow can be unpredictable.
Examples & Analogies
Consider a pipe carrying syrup. When the syrup flows slowly, it moves straight through the pipe (laminar). But if the pipe's diameter increases or the syrup is pumped faster, it starts swirling, creating turbulence and making it harder to predict how it will flow out of the pipe.
Applications of Turbulent Flow Measurement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
you can see here the photograph showing how turbulence vortices are there or eddies formations are there.
Detailed Explanation
In engineering labs, various techniques are utilized to visualize and measure turbulence. These include sophisticated imaging techniques that can capture vortices and eddies, which are characteristics of turbulent flow. Understanding these formations is crucial, as they indicate energy dissipation and can drastically affect the performance of fluid systems.
Examples & Analogies
Think of how you can observe the swirling patterns in a cup of coffee when you stir it with a spoon. This swirling motion creates vortices, similar to those in turbulent fluid flow in pipes. Just like the coffee's patterns can indicate how much energy is being spent to keep the liquid moving, engineers use similar visualizations to understand how energy is lost in fluid systems.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Turbulent Flow: Chaotic flow with eddies, impacting fluid dynamics significantly.
-
Reynolds Number: Critical parameter for classifying flow types and predicting behavior.
-
Laminar Flow: Defined as smooth, orderly flow with distinct layers.
-
Transitional Flow: The state of flow between laminar and turbulent, occurring at medium Reynolds numbers.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a pipe, if the diameter increases, the Reynolds number increases if the flow rate remains constant, thus possibly transitioning the flow to turbulent.
-
Water flowing in a river exhibits both turbulent and laminar flow characteristics, with varying velocities and obstructions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In pipes of size, flows can shift, smooth to chaotic, oh what a rift! Less than twenty-three, order we see, over four-thousand, chaos runs free!
📖 Fascinating Stories
-
Imagine a lazy river (laminar flow) where leaves float smoothly. Then, picture a busy torrent (turbulent flow) where everything is mixed and swirling vigorously.
🧠 Other Memory Gems
-
R.E.C: Reynolds, Energy, Chaos – to remember the key aspects of turbulent flow.
🎯 Super Acronyms
R.E.A.C.T – Reynolds explains and classifies turbulence.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Turbulent Flow
Definition:
A type of flow characterized by chaotic, irregular fluid motion, involving eddies and vortices.
-
Term: Reynolds Number
Definition:
A dimensionless number used to predict flow patterns in different fluid flow situations; calculated as the ratio of inertial forces to viscous forces.
-
Term: Laminar Flow
Definition:
A smooth and orderly flow where fluid moves in parallel layers, unaffected by turbulence.
-
Term: Transitional Flow
Definition:
A flow regime that occurs between laminar and turbulent flow, typically defined by Reynolds numbers between 2300 and 4000.