Using Linear Momentum Equations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Momentum Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're starting to delve into linear momentum equations, which are highly relevant in fluid mechanics. Can anyone tell me why these equations are important?

They help us understand how forces affect fluid movement, right?

Exactly! Understanding the forces acting on fluids allows us to predict flow behavior, especially in systems like pipes. Remember the acronym FLUID: 'Forces and Losses Understood in Dynamics.'

What kinds of forces are we talking about?

Great question! We're considering both inertial forces, which result from the fluid's mass and acceleration, and viscous forces, related to the fluid's viscosity. Can anyone tell me how these ideas relate to Reynolds number?

Reynolds number helps determine if the flow is laminar or turbulent, right?

Exactly! It's a key parameter in characterizing flow types, influencing our calculations in momentum equations.

In summary, linear momentum equations help us relate forces and motion of fluids and are critical for analyzing losses during flow through pipes.
Major vs. Minor Losses
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's move on to discuss major and minor losses in fluid systems. Who can define what major losses are?

Major losses are typically due to friction in the pipe, right?

Correct! These losses are significant because they are primarily driven by friction in the flow. What about minor losses?

Those come from fittings, bends, and valves?

Yes! Minor losses can add up quickly if not accounted for in system design. To help remember this, you might use the mnemonic MEAN: 'Minor Energy Added by Accessories and Networks'.

How do we calculate these losses?

We can start with experimental data and use theoretical principles like Bernoulli’s equation. Analyzing pressure differences and flow velocities helps quantify these losses.

Summarizing again, major losses mainly come from friction while minor losses arise from fittings, and both need to be calculated for efficient design.
Applying Bernoulli’s Equation and Momentum Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss how we can apply Bernoulli's equation and the linear momentum equations to solve real-world problems. Can anyone summarize Bernoulli's equation?

It's about the conservation of energy in flowing fluids, showing the relationship between pressure, velocity, and height.

Exactly! We can use it to analyze flow at different points in a system, focusing on changes in pressure and speed. What do we need to keep in mind when applying these equations?

We have to ensure the flow is along a streamline for Bernoulli's to hold, right?

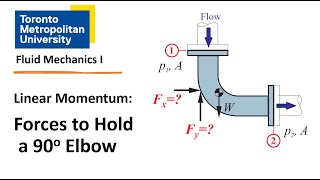
Correct, right! And for momentum equations, we must choose control volumes wisely to simplify calculations. Who can explain what a control volume is?

It's a defined region we analyze to account for mass and momentum flow, right?

Exactly! And when we set up our control volumes properly, we can analyze energy losses more effectively. Remember the acronym C-V for 'Control Volume' to keep that concept clear.

In summary, applying these equations correctly ensures accurate modeling of fluid systems, leading to better designs and lower energy costs.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, students learn how to apply linear momentum equations in fluid mechanics, focusing on calculating energy losses due to friction and fittings in pipe systems. The section emphasizes the importance of identifying major and minor losses and how to quantify them through experimental setups and theoretical principles.
Detailed
Using Linear Momentum Equations
Overview
This section provides insights into the application of linear momentum equations within fluid mechanics, particularly in the analysis of losses that occur in pipe fittings. Understanding these concepts is crucial for engineers, especially those involved in designing efficient fluid transport systems.
Key Concepts
- Major Losses: Frictional losses occurring due to the flow of fluid in pipes, primarily influenced by the pipe material and flow velocity.
- Minor Losses: Additional energy losses that arise from fittings, bends, valves, and contractions in the pipe system. These losses can be significant and must be accounted for in system designs.
- Reynolds Number: A dimensionless number that helps categorize flow regimes (laminar, transitional, turbulent) based on inertia and viscous forces.
Significance
Students will learn to quantify these losses through experiments, applying principles like Bernoulli’s equation and linear momentum equations. Proper understanding of these principles aids the design of more effective water supply systems, mitigating energy losses and ensuring optimal performance.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Linear Momentum Equations
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now if you look it I am just talking about how to use linear momentum and Bernoulli’s equations which is energy equations. So to apply this energy equations what I should do it, I take a streamline. Along the streamline I should apply the Bernoulli’s.
Detailed Explanation
This chunk introduces the concept of applying linear momentum equations and Bernoulli's equations in fluid mechanics. The key point is that when dealing with fluid flow, particularly along a streamline, you should use Bernoulli’s equations to analyze how energy is converted and conserved in the flow. Understanding how this works is crucial for solving fluid dynamics problems effectively.
Examples & Analogies
Imagine a water slide at a water park. As you slide down, the gravitational potential energy you had at the top converts into kinetic energy, making you go faster as you reach the bottom. Similarly, in fluid flow, as the fluid moves from one point to another along a streamline, energy transitions can be analyzed using these equations.
Control Volume in Fluid Dynamics
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Not here are there okay. Similar way if I am to apply the linear momentum equations or other mass of conservations I should consider the control volume is much bigger than affected area so that I can get it, this effect should not be there.
Detailed Explanation
In fluid dynamics, a control volume is a defined space in which you analyze the behavior of fluids. The importance of selecting an appropriate control volume—one that encompasses the flow region without being affected by external forces or changes—is crucial. By choosing a larger control volume relative to the area affected by the fluid, you simplify calculations and minimize the influence of interference on your analysis.
Examples & Analogies
Think of a sealed container of gas. If you want to study how the gas behaves when compressed, you wouldn't focus on just a tiny part of the gas; instead, you'd look at the whole container to understand pressure changes. Similarly, in fluid mechanics, a well-defined control volume helps ensure that you're examining all relevant aspects of fluid behavior.
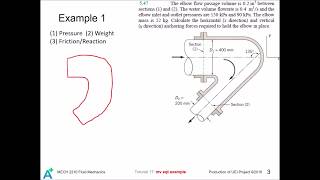
Application of Bernoulli’s Equation
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So I can use this control volume to apply the mass conservation equations or linear momentum. Exactly same way I can use this control volume still up to this spot, apply it. Please do not take the control volume like this, which is totally wrong.
Detailed Explanation
This chunk emphasizes the application of Bernoulli's equation and conservation laws within the chosen control volume. It highlights the need to maintain a control volume that effectively describes the flow without introducing errors. A common mistake would be choosing a control volume that doesn’t align with the flow direction or involves curved streamlines, which would yield incorrect results.
Examples & Analogies
Imagine surveying the flow in a river. If you set up a measuring section that’s too narrow or misaligned with the river’s flow, you could misjudge the river’s speed and depth. Choosing the right section to monitor ensures that you gather accurate data, just like selecting the right control volume helps you analyze fluid behavior correctly.
Controlling Streamlines for Analysis
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So to take a appropriate the control volumes, we should have a knowledge of how the flow happens it, how the flow behaviors are happens it, where the vortex is happening, where the flow lines the streamlines are parallel.
Detailed Explanation
Understanding the behavior of flow—such as the presence of vortices and the nature of streamlines—is vital for choosing the correct control volume. Recognizing where streamlines are parallel indicates regions with uniform flow, allowing for more accurate application of equations. Knowledge of these flow characteristics aids engineers in making effective calculations.
Examples & Analogies
Consider an airplane in flight; pilots and engineers must know how air flows around the wings (streamlines) to optimize performance and safety. Just like they understand where the airflow is stable and where turbulence occurs, fluid dynamics practitioners must gauge flow characteristics to apply equations effectively.
Key Concepts
-
Major Losses: Frictional losses occurring due to the flow of fluid in pipes, primarily influenced by the pipe material and flow velocity.
-
Minor Losses: Additional energy losses that arise from fittings, bends, valves, and contractions in the pipe system. These losses can be significant and must be accounted for in system designs.
-
Reynolds Number: A dimensionless number that helps categorize flow regimes (laminar, transitional, turbulent) based on inertia and viscous forces.
-
Significance
-
Students will learn to quantify these losses through experiments, applying principles like Bernoulli’s equation and linear momentum equations. Proper understanding of these principles aids the design of more effective water supply systems, mitigating energy losses and ensuring optimal performance.
Examples & Applications
In a pipe carrying water, if the Reynolds number is above 4000, the flow is considered turbulent, leading to higher major losses.
When calculating energy losses in a pipeline network, both major losses (due to friction) and minor losses (due to valves and bends) must be considered for accurate design.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In water pipes, friction's a blight, major losses come from the fight.
Stories
Imagine a river flowing quite wide, encountering rocks — major losses abide, but with tiny bends and turns so tight, we face minor losses in the daylight.
Memory Tools
Use 'MEAN' to remember Minor Energy Added by Accessories and Networks.
Acronyms
C-V means Control Volume — the area of focus in analyzing fluid dynamics.
Flash Cards
Glossary
- Linear Momentum Equation
An equation that describes the motion of a fluid by relating forces acting on it to changes in momentum.
- Major Losses
Energy losses in a pipe system largely due to friction between the fluid and the pipe walls.
- Minor Losses
Energy losses occurring from fittings, valves, and bends in a pipe system.
- Reynolds Number
A dimensionless number used to predict flow patterns in different fluid flow situations.
Reference links
Supplementary resources to enhance your learning experience.
