Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Vortex Formation
Unlock Audio Lesson
Welcome class! Today we're diving into vortex formation within pipe flows. Can anyone explain what a vortex is?
Isn't a vortex a swirling motion of fluid around an axis?
Exactly! And when we talk about pipes, understanding vortex formation is crucial because it affects energy losses. We quantify vortices using the Reynolds number. Can anyone tell me the thresholds for laminar and turbulent flow?
A Reynolds number below 2300 indicates laminar flow, and above 4000 indicates turbulent flow.
Correct! And in between is the transitional zone. Remember: LOW for Laminar; HIGH for Turbulent. Let’s feel the energy transformation in vortices!
How do we visualize these vortices in the fluid?
Great question! We use concepts like virtual fluid balls to illustrate these complex flows. It's also fundamental in applying Bernoulli's equations effectively. Let's summarize: Vortices lead to energy loss and can be quantified using Reynolds numbers.
Energy Losses in Pipe Systems
Unlock Audio Lesson
Now, let's discuss energy losses in pipe systems. Can anyone define the difference between major and minor losses?
Major losses are due to friction in longer pipes, while minor losses arise from fittings like valves or bends.
Exactly! Major losses tend to dominate in long flows. Think of minor losses as the 'little bumps' every time the fluid isn't flowing in a straight line. Who can give an example of a minor loss?
Bends and valves are good examples!
Perfect! Vortex formations contribute to these losses. Remember how the virtual fluid balls interact with these fittings, creating eddies? It’s time to quantify these losses.
How do we actually measure energy loss?
Excellent question! We measure with pressure differences using manometers, then apply Bernoulli’s equation appropriately. To summarize: Differences in pressure and flow configuration control our losses.
Learning from Moody's Chart
Unlock Audio Lesson
We must also address Moody's chart, a crucial tool for determining friction factors. Can someone explain how we use it?
We find the Reynolds number and relative roughness to discover the corresponding friction factor.
Exactly right! It is essential in understanding frictional losses. Remember the relationship helps us link energy losses to design parameters and pipe sizes.
What if we lack the chart?
Good point! Even without it, we have implicit equations to estimate friction factors. However, it’s tricky since they require iterations. So, always prefer the chart if available.
Summarizing: Moody's chart offers an efficient way to determine friction factors.
You got it! Vortex formation, energy losses in pipes, and computation with Moody's chart are intertwined. Keep those connections clear!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the focus is on vortex formations and the role of virtual fluid balls in understanding fluid behavior in pipe systems. Various aspects such as energy losses in minor and major pipe fittings, the impact of turbulent flow as quantified by Reynolds numbers, and the utilization of Moody's chart are explored.
Detailed
Detailed Summary
The section delves into the intricate phenomena of vortex formation in fluid dynamics, specifically within pipe flow systems.
Key Points Covered:
- Vortex Formation: Vortices and turbulence in fluid flow are primarily quantified through Reynolds numbers. Here, a Reynolds number less than 2300 indicates laminar flow, while greater than 4000 indicates turbulent flow. Between 2300 and 4000 signifies a transition point.
- Virtual Fluid Balls: The concept of virtual fluid balls is introduced to represent the flow streamlines in complex fluid dynamics. This concept assists in applying Bernoulli’s equations effectively along streamlines.
- Energy Losses: The section outlines the difference between major losses (due to friction in pipes) and minor losses (attributable to fittings like bends or valves). Understanding these losses is essential for optimizing designs in hydraulic systems.
- Moody's Chart: Reference to Moody's chart facilitates the computation of friction factors based on Reynolds numbers and relative roughness of pipes, assisting engineers in predicting energy losses.
- Vortex Implications: The impact of vortices on energy loss and their relationship with flow direction and configuration (e.g., contractions and expansions in pipes) is highlighted, emphasizing how students can utilize this knowledge in real-world applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Vortex Formation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Here again I have to repeat it to tell it the virtual fluid balls to understand how the vortex formations happens within a pipe flow systems, okay. Like the last class I discussed about the pipe flow systems, when I am considering it, the pipe, a horizontal pipes and because of the turbulence how the eddies formations happen. These are eddies, these are eddies formations happening it and those what we try to understand because if there is a horizontal flow is coming going out and we quantify in terms of the balls moving with disintegrated, integrated concept.
Detailed Explanation
In this chunk, the focus is on the concept of vortex formation in pipe systems through the lens of virtual fluid balls. The idea is that, in a turbulent flow within horizontal pipes, vortices and eddies (which are swirling motions of fluid) form due to the irregular flow. The 'virtual fluid balls' concept allows us to understand how these eddies disrupt the flow by visualizing them as discrete units of fluid. When we study fluid mechanics, it's essential to recognize how these formations occur, as they play a significant role in the flow dynamics and pressure loss within pipes.
Examples & Analogies
Imagine a packed concert hall where people are moving along aisles to enter or exit. Just like those people bump into each other, creating swirling patterns, fluid particles can collide and create these 'vortex formations.' In simple terms, if you visualize the people as fluid molecules, their crowded, swirling movement represents the eddies in fluid flow.
Using Virtual Fluid Balls to Understand Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
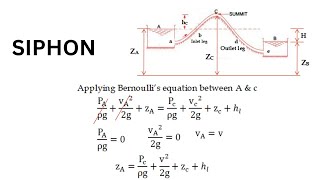
The same virtual fluid ball concept to define the flow streamlines. Because, as you know it when you try to apply the Bernoulli’s equations the first assumption is that you should apply along a streamline. Or if you consider the flow is irrotational.
Detailed Explanation
This section emphasizes how virtual fluid balls help define flow streamlines. It points out that when applying Bernoulli’s equations, which relate pressure, velocity, and height in fluid flow, one has to assume that the flow occurs along a streamline – a path that fluid particles follow. In many cases, assume the flow is 'irrotational,' meaning there is no swirling or rotating motion at any given point along the streamline which simplifies calculations.
Examples & Analogies
Consider a smooth, flowing river. The river's surface is like a streamline where the water molecules move in a straight path. If you drop a piece of fruit into the river, it follows this path without swirling or turning. This is similar to how we can think of fluid balls moving along streamlines in physics.
Vortex Zones and Energy Loss
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us go back to the Lewis Moody 1944 Princeton University, USA. What he has developed is from the experimental data. If you try to look it, he has not pulled out only his experimental data, but long back the data from others researchers. All the data he combined it for the developing this Moody's charts to compute friction factors, compute the friction factor, the flow through the pipes.
Detailed Explanation
This part introduces the Moody chart, which is a graphical representation developed to help engineers and scientists compute the friction factor in pipe flow. The friction factor is crucial because it relates to energy loss due to the flow resistance caused by the internal surface of the pipe and any vortex formations. The chart combines data from various sources to provide a standardized reference for different flow conditions, including laminar and turbulent flows.
Examples & Analogies
Think of the Moody chart as a recipe book for understanding how much resistance the pipes will encounter as fluids flow through them. Much like when baking, where you might refer to a recipe for the correct amount of ingredients, engineers use the Moody chart to find out how much 'friction' they should expect based on the type of fluid flow.
Energy Loss due to Vortex Formation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us look it how would it happens it. That again I am considering virtual fluid balls okay. If I consider the virtual fluid balls, the balls which is going very close to the wall, which will go straight and inject here as a tangential and go like this, okay. What will happen to this? Here also we have the particular liquid, but that liquid will have a vortex formation.
Detailed Explanation
In this section, the text discusses how virtual fluid balls near the pipe walls interact with the flow and induce vortex formations. When fluid moves inside a pipe, especially when it’s near the walls, it can create small whirlpool-like motions. These vortices contribute to energy loss in the system because they disrupt the smooth flow of fluid, leading to increased friction against the pipe walls and a decrease in pressure.
Examples & Analogies
Imagine how water swirls down a drain after you pull out the plug. Just as the swirling water creates a disruption that slows down the draining process, the vortex formations near the walls of pipes cause energy losses that can affect the efficiency of fluid transportation.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Vortex formation: Essential in defining energy loss in fluid flow, quantified by Reynolds number.
-
Virtual fluid balls: Used to illustrate flow behavior within pipes and aid in applying Bernoulli's equation.
-
Energy losses: Differentiated into major (friction along pipes) and minor losses (from fittings).
-
Moody's chart: A pivotal tool to calculate friction factors linked to energy loss and design considerations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When water flows through a pipe bend, vortex formations can lead to additional minor losses.
-
Estimating friction loss using Moody's chart requires knowledge of the Reynolds number and the relative roughness of the pipe.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Vortex in the pipe, swirling round and round, energy losses mean less flow can be found!
📖 Fascinating Stories
-
Imagine sailing in a river. Sharp turns create whirlpools that slow down your boat, just like bends in pipes create energy losses.
🧠 Other Memory Gems
-
FLOWS: Flow Loss Occurs With Fittings (to remember minor losses).
🎯 Super Acronyms
V.E.L.O.C.I.T.Y
- Vortex Energy Losses Obstructing Flow in Complex Internal Turbulent Yield.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Vortex Formation
Definition:
A phenomenon where fluid swirls around an axis within a flow, causing energy losses in pipe systems.
-
Term: Reynolds Number
Definition:
A dimensionless number used to predict flow patterns in different fluid flow situations.
-
Term: Virtual Fluid Balls
Definition:
A conceptual model used in fluid dynamics to understand flow streamlines and vortex behavior.
-
Term: Bernoulli’s Equation
Definition:
An equation that describes the relationship between pressure, velocity, and height in flowing fluids.
-
Term: Moody's Chart
Definition:
A graphical representation that provides friction factors for pipe flow based on the Reynolds number and relative roughness.
-
Term: Major Losses
Definition:
Energy losses in pipe flow primarily due to friction along the length of the pipe.
-
Term: Minor Losses
Definition:
Energy losses occurring in fittings, bends, and changes in flow direction in pipe systems.