Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydraulic Jumps
Unlock Audio Lesson
Good morning class! Today, we'll explore hydraulic jumps, a fascinating phenomenon in fluid mechanics. Can anyone tell me what happens in a hydraulic jump?
Isn't it when water flows from a faster, shallow state to a slower, deeper state?
Exactly! That's called transitioning from supercritical to subcritical flow. And what is the Froude number for supercritical flow?
It's greater than 1, right?
Yes! And for subcritical flow, the Froude number is less than 1, indicating a slower flow dominated by gravity. Great job! Let's summarize this: hydraulic jumps happen when we switch from fast to slow flow, indicating energy loss.
Energy Loss in Hydraulic Jumps
Unlock Audio Lesson
Now, energy loss during hydraulic jumps is critical for design. Can anyone explain what specific energy involves?
Isn't specific energy a combination of flow depth and velocity?
Correct! The specific energy equation is E = y + (v² / 2g). How can we estimate energy losses due to a hydraulic jump?
We compare specific energy before and after the jump, right?
Absolutely! Energy loss can be expressed as hL = E1 - E2. Make sure to remember: understanding energy loss is critical for effective design!
Applications of Hydraulic Jumps
Unlock Audio Lesson
Hydraulic jumps are not just academic; they have practical applications. Can anyone suggest where we might see hydraulic jumps in real life?
In spillways and dams?
Exactly! They help with energy dissipation, preventing erosion. And what happens downstream of a dam due to these jumps?
There’s a lot of turbulence and mixing!
Right! And this turbulence aids in aerating the water. Remember, engineers often design these jumps to improve mixing for various applications!
Calculating Hydraulic Jump Characteristics
Unlock Audio Lesson
Let's look at how to calculate the flow depths and velocities before and after a hydraulic jump. If we know y1 and v1, how can we find y2 and v2?
We can use mass conservation equations!
Correct! The equation v1y1 = v2y2 helps us here. Let’s practice solving a problem together involving these calculations.
How about we consider an example where we use known values to determine the unknowns?
Great idea! By solving together, we’ll see how these concepts apply practically.
Summary of Hydraulic Jump Dynamics
Unlock Audio Lesson
As we conclude, what are the essential takeaways about hydraulic jumps?
They result from transitioning from supercritical to subcritical flow!
And they cause energy losses that need to be calculated for design purposes.
Exactly – excellent summary, everyone! Remember their applications in dam structures and energy dissipation. Keep these concepts in mind as we move on to the next topic!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Hydraulic jumps occur when fluid transitions from supercritical to subcritical flow, producing significant turbulence and energy loss. This section describes the conditions for hydraulic jumps, key equations for analyzing these phenomena, and their importance in canal and spillway design.
Detailed
Characteristics of Hydraulic Jumps
In this section, we delve into hydraulic jumps within open channel flow, emphasizing their formation and significance. Hydraulic jumps occur as fluid transitions between supercritical and subcritical flow conditions, specifically when the Froude number changes from greater than 1 to less than 1.
Key Characteristics
- Supercritical Flow: Defined by a Froude number greater than 1, which indicates rapid flow where gravitational forces are weaker than inertial forces.
- Critical Flow: Occurs at a Froude number equal to 1, representing a point of equilibrium between gravitational and inertial forces.
- Subcritical Flow: Exhibited when the Froude number is less than 1, where gravitational forces dominate, allowing for slower, deeper flows.
The transition between these states leads to significant turbulence and energy dissipation, characterized as hydraulic jumps. These jumps can cause substantial mixing, making them advantageous for aeration and chemical reactions in engineering applications.
Energy Considerations
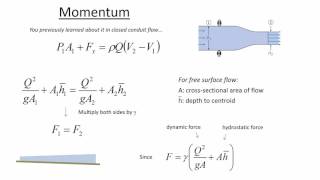
Energy loss during hydraulic jumps can be quantified. Understanding the specific energy concepts (E) allows engineers to design effective structures that accommodate hydraulic jumps while minimizing energy loss. The relationship between upstream and downstream conditions gives crucial insights into designing effective and efficient hydraulic systems. By applying mass and energy conservation equations, we can analyze the characteristics of hydraulic jumps both theoretically and practically.
Overall, hydraulic jumps are vital in civil engineering, informing the design of spillways, canals, and drainage systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Hydraulic jumps occur when a high-speed flow transitions to low-speed flow, particularly when moving from supercritical to subcritical conditions. This transition results in visible turbulence and energy loss.
Detailed Explanation
Hydraulic jumps are phenomena that happen in open channel flows, particularly during rapid changes in flow conditions. When water flows quickly and then encounters a slower-moving body of water, it forms turbulence and creates frothy structures which we recognize as hydraulic jumps. These jumps indicate a transfer of energy from the flowing water to turbulent motion, leading to energy losses.
Examples & Analogies
Think of hydraulic jumps like a car suddenly hitting a large puddle on the road; the car splashes up water and slows down quickly. The puddle represents lower velocity water, which creates disturbance—similar to what happens during a hydraulic jump.
Flow Conditions and Froude Numbers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In hydraulic jumps, flow conditions are characterized by the Froude number, which is the ratio of the flow's inertia to gravity forces. A Froude number less than 1 indicates subcritical flow, while greater than 1 indicates supercritical flow.
Detailed Explanation
The Froude number (Fr) is crucial for classifying the flow conditions. When Fr < 1, the flow is calm and allows surface waves to move upstream. Conversely, when Fr > 1, the flow is rapid and waves cannot travel against the flow. Hydraulic jumps occur between these two states when the supercritical flow suddenly transitions into subcritical flow, showcasing how speed changes influence flow behavior.
Examples & Analogies
Imagine a river flowing fast down a slope (supercritical) that suddenly hits a flat area (subcritical). The fast-moving water has to slow down, creating turbulence and splashes, similar to how water splashes in a tub when you rush to fill it but then stop the flow suddenly.
Energy Losses during Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Energy losses occur during hydraulic jumps due to turbulent flow caused by abrupt changes in velocity. The energy loss can be quantified using specific energy principles.
Detailed Explanation
As water transitions from supercritical to subcritical flow, it experiences significant energy loss, resulting from turbulence and mixing of water. When analyzing this energy loss, engineers use the concept of specific energy, which involves measuring total energy (potential and kinetic) related to the flow depth and velocity. This helps in understanding how much energy is dissipated during hydraulic jumps.
Examples & Analogies
Think of it like a roller coaster. When the coaster goes from a steep drop (high speed, low energy) to a level surface, it loses energy quickly, producing a thrill factor (splashing water and turbulence), similar to the turbulence observed in a hydraulic jump.
Practical Implications of Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Hydraulic jumps are significant in engineering designs, particularly in spillways and channels. They help mix chemicals in wastewater treatment and reduce the energy of the water flowing downstream.
Detailed Explanation
Engineers often design channels and spillways around the concept of hydraulic jumps to ensure effective flow management. The jumps help in reducing flow velocities and dissipating energy, which protects structures and allows for efficient mixing and treatment processes in hydraulic systems. By understanding where and how these jumps occur, engineers can better design structures that utilize these natural phenomena.
Examples & Analogies
Imagine mixing a drink with ice. As you stir (similar to a hydraulic jump), the ice mixes into the liquid, cooling it down efficiently. In water treatment, hydraulic jumps create necessary turbulence to mix chemicals effectively, ensuring a better treatment.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic Jump: A transition from supercritical to subcritical flow that results in energy dissipation.
-
Specific Energy: The total mechanical energy (potential plus kinetic) per unit weight.
-
Froude Number: A dimensionless number to describe flow regimes, critical for analyzing hydraulic jumps.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Flow through a spillway exhibits hydraulic jumps as water flows from the dam.
-
Example 2: A hydraulic jump is used in aeration processes to enhance mixing in wastewater treatment.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Jumping flows that go below, turbulent waters start to flow.
📖 Fascinating Stories
-
Imagine a river rushing swiftly down a slope, but then it hits an obstacle and leaps up, creating tumultuous waves—the hydraulic jump forming exciting splashes downstream.
🧠 Other Memory Gems
-
Remember: 'SCS' - Supercritical, Critical, Subcritical - the order of flow states in hydraulic jumps.
🎯 Super Acronyms
Frog
- Froude number governs flow states—greater than one for supercritical!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Jump
Definition:
A sudden transition in flow regime, occurring when fluid moves from supercritical to subcritical flow, causing turbulence and energy dissipation.
-
Term: Froude Number
Definition:
A dimensionless number used to compare inertial and gravitational forces in fluid flow, indicating flow regimes.
-
Term: Specific Energy
Definition:
The total energy per unit weight of fluid, calculated as the sum of potential energy due to elevation and kinetic energy due to flow velocity.