Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydraulic Jumps
Unlock Audio Lesson
Today, we will focus on hydraulic jumps. Can anyone explain what a hydraulic jump is?
Isn't it the sudden change in the flow of water in channels?
Exactly! It's a transition from supercritical to subcritical flow. This indicates a significant increase in flow depth and turbulence. The jump generates energy loss, which is crucial for engineers to account for in designs.
How does the Froude number relate to hydraulic jumps?
Great question! The Froude number helps classify the flow. We use it to determine if we are in subcritical, critical, or supercritical flow conditions. A higher Froude number shows supercritical flow, prompting the jump.
Energy Loss in Hydraulic Jumps
Unlock Audio Lesson
Now, let's talk about energy losses. Can someone summarize why energy dissipation occurs?
It happens because of the turbulence created when water transitions from supercritical to subcritical states.
Perfect! Energy losses can be calculated using the specific energy before and after the jump. The energy loss, HL, equals E1 (upstream energy) minus E2 (downstream energy).
What formula do we use for specific energy?
Specific energy, E, is given by E = y + v^2/(2g), where y is the flow depth and v is the velocity. A reminder, since energy loss will occur, always check your calculations!
Example Problems
Unlock Audio Lesson
Let's solve an example problem together. If we have a hydraulic jump and know y1 = 1m and v1 = 10m/s, how do we find y2 and v2?
First, we should check the Froude number to see if it’s supercritical.
Correct! The formula for the Froude number is Fr = v/(√(gy)). If Fr > 1, it's supercritical, indicating a jump occurs.
Then we can use the conservation equations to find out y2 and v2.
Absolutely! Using the mass conservation and momentum equations, we can derive v2 and y2 after the jump.
What would the energy losses be like for this scenario?
The energy losses can be calculated after finding specific energy values for y1 and y2 using the formula I mentioned earlier.
Hydraulic Jump Design Considerations
Unlock Audio Lesson
Finally, how do hydraulic jumps affect engineering designs in channels?
They need to be designed to handle the turbulence and energy dissipation, right?
Exactly! Engineers must consider these when designing spillways or drainage channels to prevent erosion and ensure stability.
Can we use what we learned about hydraulic jumps in real life?
Definitely! Applications include managing floodwater, conservation of ecosystems in rivers, and designing efficient irrigation systems.
Thanks for the clarification, it ties in well with what we're learning about fluid dynamics!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Hydraulic jumps are critical occurrences in open channel flow that result from transitions from supercritical to subcritical flow. The section presents the physics behind hydraulic jumps, conservation equations, and practical examples to calculate flow parameters before and after jumps, including energy losses and system design considerations.
Detailed
Detailed Summary
Hydraulic jumps are significant phenomena observed when water transitions from supercritical to subcritical flow. These jumps are characterized by turbulent mixing and energy dissipation, and understanding them is crucial for civil engineering applications involving open channel flow, such as spillways and irrigation systems.
In this section, we delve into the specific conditions leading to hydraulic jumps, utilizing key concepts such as the Froude number, flow depth, and specific energy. The Froude number indicates whether the flow is subcritical (F<1), critical (F=1), or supercritical (F>1), influencing how the energy and flow velocity change throughout a system. Through example problems, we apply mass conservation and momentum principles to evaluate flow parameters before and after the jump, assess energy losses, and analyze spatial conditions for effective design and system management.
The discussion emphasizes calculation methods for flow parameters such as downstream velocity and depth, establishing relationships between upstream and downstream states across the jumps. Students are encouraged to engage with practical examples demonstrating real-world implications of hydraulic jumps and efficient channel design.
Youtube Videos
![Open Channel Flow 38 - {How to calculate sequent depth and energy loss in hydraulic jump problem]](https://img.youtube.com/vi/eAjApbk4NhA/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
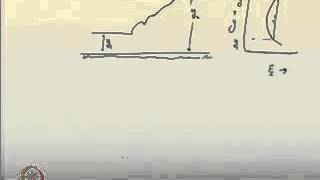
If you look at the hydraulic jumps, if you have a more or less the horizontal surface okay more or less you have a horizontal surface and you have a sluice gate okay it is a gate operating it. the flow is coming from this side it has a depth okay. After that you can see that flow will be like a jet flow it will happen like this okay. This is the gate which is we are operating this is what a gate the flow is coming from this side and going out. So we can see that the flow will move like a jet type of flow.
Detailed Explanation
Hydraulic jumps occur when fluid flows over a sluice gate causing the flow to transform from a high-energy state into a lower energy state, resulting in a significant change in flow characteristics. Initially, the flow is steady and streamlined as it moves toward the sluice gate. Upon passing through the gate, the fluid experiences a rapid change in velocity and energy, leading to the formation of turbulent eddies and energy dissipation, which we observe as a 'jump' in the water surface.
Examples & Analogies
Imagine water flowing smoothly down a slide and suddenly hitting a flat pool of water. As it enters the pool, the water splashes and creates a turbulent surface, just like a hydraulic jump occurs when water passes through a sluice gate.
Understanding Flow Characteristics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I follow as a steady flow. So the mass conservation equations give me that very basic thing that rho is the density multiplied with the q that is mass inflow is equal to mass outflow. In this case if this is the v1 velocity and this is the v2 velocity so I can write it rho v1 y1 and b is a perpendicular depth or the width is equal to rho v2 y2 and b. So b will cancel out rho as an incompressible flow and the steady flow. So we have a v1 y1 is equal to v2 y2.
Detailed Explanation
This equation expresses the principle of conservation of mass applied to the flow before and after the jump. In a hydraulic jump, the product of the flow depth (y) and velocity (v) remains constant through the sluice gate, revealing the interactions between them during the hydraulic jump. If the depth decreases, the velocity must increase, adhering to the conservation laws.
Examples & Analogies
Think of a garden hose being slightly pinched at the end. When you decrease the area of the opening (like decreasing flow depth), the water speeds up (increasing velocity) as it shoots out of the hose. This is a practical demonstration of the principle that relates flow depth and speed in fluid dynamics.
Formation of Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When the flow passes through the supercritical to subcritical with a very limited ranges then there are a lot of turbulent structures created okay. There are a lot of mixings, the turbulent structures are necessary. created that is what we call hydraulic jump that is what is hydraulic jump there is energy losses happens it there is energy losses happen it when flow goes through the supercritical please remember supercritical to subcritical.
Detailed Explanation
The transition of flow from supercritical (high speed, low depth) to subcritical (lower speed, higher depth) creates a hydraulic jump. This abrupt change causes turbulence and mixing, contributing to energy loss. Energy dissipation in hydraulic jumps is vital for preventing erosion downstream and ensuring stability in hydraulic systems.
Examples & Analogies
This can be compared to a waterfall where water falls rapidly into a still pool. Upon hitting the pool, the water splashes up, and chaos ensues in the form of waves and currents—a hydraulic jump effect happens in nature.
Analyzing Energy Losses in Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
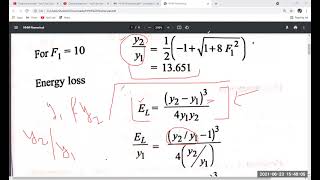
Energy losses due to the hydraulic jump is hL okay energy losses due to the hydraulic jump is hL. So very easily I can write it energy conservation E1 is equal to E2 plus hL a very simple thing. So it is very simple things to get it the energy losses okay.
Detailed Explanation
In analyzing hydraulic jumps, we apply the principle of energy conservation. The energy present before the jump (E1) is equal to the energy post-jump (E2) plus the energy lost (hL). This relationship enables engineers to quantify energy losses in hydraulic systems and design accordingly, ensuring efficiency and effectiveness.
Examples & Analogies
Consider a bungee jump where the jumper loses some energy while falling and bouncing back. Similarly, the hydraulic jump represents a loss of energy as water flows, transforming potential energy into turbulence and less useful energy, akin to the energy lost in the bungee cord.
Estimation of Flow Characteristics Post-Jump
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you know the v2 y2 we can compute the flow proud numbers as is a subcritical flow that should be less than 1 and then you can v2 y2 know it we can estimate the specific energy at the downstream levels okay.
Detailed Explanation
To compute flow characteristics after a hydraulic jump, knowing the downstream velocity (v2) and flow depth (y2) allows for calculating the Froude number, which indicates the flow regime (subcritical or supercritical). The specific energy at downstream conditions is integral to understanding how much energy is available for flow processes and management.
Examples & Analogies
Think of a river where you measure the flow rate after a series of rapids (like hydraulic jumps). The measurement helps determine the health of the flow downstream and informs decisions about water use, irrigation, or flood management.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic Jump: A phenomenon occurring when flow transitions from supercritical to subcritical conditions, resulting in turbulence and energy loss.
-
Froude Number: A key dimensionless parameter that indicates flow classification and conditions.
-
Specific Energy: The energy of flow expressed per unit weight, crucial for analyzing energy changes across hydraulic jumps.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a specific problem setup, the upstream Froude number was calculated to be 2, indicating supercritical flow before a jump.
-
A practical example involved calculating the downstream flow depth after a hydraulic jump, showcasing changes in flow conditions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When water flows fast and deep, a jump it makes, it can’t keep.
📖 Fascinating Stories
-
Imagine a river where water flows quickly. Suddenly, it faces an obstacle and leaps up, creating bubbles and a splash – this is a hydraulic jump!
🧠 Other Memory Gems
-
Froude Number = Flow's Rushing Over Under Deep Energy.
🎯 Super Acronyms
H.J. - Hydraulic Jump
- High Jumping!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Jump
Definition:
A sudden change in water flow that occurs when the flow transitions from supercritical to subcritical, resulting in turbulence and energy loss.
-
Term: Froude Number
Definition:
A dimensionless number used to compare inertial forces to gravitational forces in fluid flow, helping to classify flow conditions.
-
Term: Specific Energy
Definition:
The energy per unit weight of fluid, calculated as the sum of flow depth and kinetic energy per weight.