Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Specific Energy
Unlock Audio Lesson
Good morning class! Today, we are diving into specific energy in open channel flow. Can anyone tell me what specific energy means in this context?
Is it the energy per unit weight of the fluid?
Exactly! Specific energy combines potential and kinetic energy. It's essential for analyzing flow dynamics. Remember: E = y + (v^2 / 2g) where E is specific energy, y is the flow depth, and v is the velocity.
How does this relate to flow conditions?
Great question! The flow can be classified as subcritical, critical, or supercritical based on the Froude number. Let's break them down.
Froude Number and Flow Types
Unlock Audio Lesson
The Froude number is a critical dimensionless ratio that indicates flow regime. Can anyone recall how we calculate it?
It’s velocity divided by the square root of gravitational acceleration times flow depth, right?
"Spot on! The three conditions are:
Understanding Hydraulic Jumps
Unlock Audio Lesson
A key phenomenon in fluid mechanics is the hydraulic jump, which occurs when supercritical flow transitions to subcritical flow. Can anyone explain why this leads to energy loss?
I think it’s because of turbulence created during the transition?
Exactly! The abrupt change in depth creates turbulence, leading to energy dissipation. It’s vital for engineers to understand these jumps when designing canals and spillways.
How can we calculate the energy loss during a hydraulic jump?
You can use the energy conservation principle: E1 = E2 + hL, where hL is the energy lost. Understanding these calculations is crucial for effective engineering design.
Graphical Representation
Unlock Audio Lesson
Now let's talk about the graphical representation of specific energy. What do you think a specific energy curve looks like?
Is it a curve that shows how energy varies with discharge?
Yes! We can plot specific energy against flow depth at constant discharge to show the relationship. The curve helps in visualizing the energy dynamics in flow conditions.
And this is important for designing structures, right?
Exactly! Engineers use it to design canals efficiently, minimizing energy losses and ensuring safe flow conditions.
Application and Design Implications
Unlock Audio Lesson
Finally, let’s summarize how understanding specific energy directly applies to engineering design.
It helps us manage flow in waterways more effectively.
Correct! By knowing how energy behaves, we can design structures like spillways that manage flow efficiently, reducing risks.
So understanding this concept is essential for ensuring public safety?
Absolutely! Safeguarding infrastructure requires a solid grasp of these principles. Let’s keep these in mind as we move to the next topic.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section focuses on specific energy in open channel flow, explaining how it varies with flow depth and the significance of critical conditions such as subcritical and supercritical flows. It further explores the graphical representation of specific energy, energy losses during hydraulic jumps, and their engineering implications.
Detailed
Graphical Representation of Specific Energy
This section provides an in-depth look at the concept of specific energy in open channel flow. Specific energy is defined as the total mechanical energy per unit weight of fluid relative to the datum, expressed as the sum of potential energy (height) and kinetic energy (velocity).
Key points discussed include:
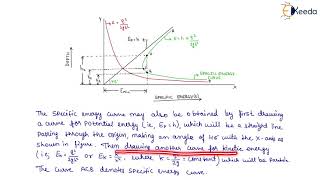
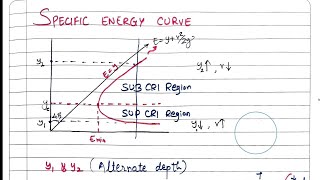
- Specific Energy vs. Flow Depth: It describes the graphical relationship of specific energy to varying flow depths in a channel. The horizontal axis represents the flow depth, while the vertical axis shows the specific energy.
- Critical Flow Conditions: The section highlights three conditions of flow based on the Froude number:
- Subcritical Flow (Fr < 1): Characterized by lower velocities, where surface waves can move upstream.
- Critical Flow (Fr = 1): Occurs at the critical depth where flow velocity equals wave speed.
- Supercritical Flow (Fr > 1): Exhibits higher velocities, and surface waves cannot move upstream.
- Hydraulic Jumps: The section discusses how transitions between these flow conditions induce hydraulic jumps, which are sudden changes in flow depth and energy. Energy loss occurs when flow changes from supercritical to subcritical, creating turbulence and mixing, significant for practical engineering designs.
- Graphical Analysis and Design Implications: It explains how to utilize specific energy curves to determine design parameters for hydraulic structures like canals and spillways, emphasizing efficiency in construction and flow management.
The significance of these concepts is crucial for civil engineering applications, especially in hydrostructure design and understanding water flow dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Specific Energy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The basic idea to know it, the flow depth variations in open channels, the velocity variations, how the velocity changes it, how much of energy losses, okay. losses is happening it because of the flow and mostly it is governed by the gravity forces and the frictional forces as I discussed earlier.
Detailed Explanation
In open channel flow, specific energy is a critical concept that describes the energy available to the flow at a given depth. We need to understand how the flow depth (the height of the water above the channel bottom) can affect both the flow velocity (the speed of the water) and energy losses. Energy losses in this context primarily arise due to the gravitational pull on the water and friction between the water and the channel sides or bottom. Essentially, the greater the depth of water, the more energy is available for flow, but this energy can be lost due to friction as the water moves.
Examples & Analogies
Think of specific energy like the potential energy of a rolling ball. The deeper the water, like a steeper hill, the more energy it has available to flow. However, as the ball rolls down, it encounters friction, much like water encounters resistance from the channel, causing it to lose energy.
Critical Flow Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Subcritical flow occurs when the Froude number is less than 1, meaning the flow's velocity is less than the wave speed. Critical flow is when the Froude number equals 1, indicating a balance between the flow velocity and wave speed. Supercritical flow occurs when the Froude number is greater than 1, meaning the flow is faster than the wave speed.
Detailed Explanation
The Froude number, a dimensionless number used in fluid mechanics, indicates the flow regime in open channels. When it is less than 1 (subcritical flow), the flow is calmer and can respond readily to changes. At exactly 1 (critical flow), the flow transitions, creating efficient energy use. When exceeding 1 (supercritical flow), the flow becomes rapid and can have turbulent characteristics. Understanding these classifications helps engineers design better channels and predict flow behavior in water bodies.
Examples & Analogies
Imagine a car on a highway. When the speed limit is low (subcritical, less than 1), the traffic flows smoothly. As cars reach a certain speed (critical, equal to 1), they flow efficiently without break. When cars go beyond the speed limit (supercritical, greater than 1), they start zooming past, creating potential hazards and turbulence just like how water can become chaotic and turbulent in supercritical flow.
Hydraulic Jumps and Energy Losses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When a flow transitions from supercritical to subcritical, it creates a hydraulic jump. This jump can lead to significant energy losses, which can be analyzed using specific energy concepts.
Detailed Explanation
A hydraulic jump occurs when the flow transitions rapidly from a high-velocity, low-energy state (supercritical) to a slower, higher-energy state (subcritical). In this process, energy is dissipated, often in the form of turbulence and heat. Engineers must consider these jumps when designing channels to account for energy losses and ensure proper flow management. Understanding where these jumps occur helps in designing structures like dam spillways where controlled flow is critical.
Examples & Analogies
Consider a waterslide. If you slide down quickly (supercritical), you'll splash into a pool at the bottom. Sometimes, the water may create a big splash as you enter the water (hydraulic jump). This splash represents energy being lost to the environment. If the slide is too steep and you go super fast, the impact can be dangerous, similar to how engineers must control water flows to prevent damage during hydraulic jumps.
Graphing Specific Energy Curves
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The specific energy curve is a graphical representation of specific energy versus flow depth. It illustrates how energy changes with different flow depths for a given discharge.
Detailed Explanation
A specific energy curve visually represents the relationship between specific energy and flow depth for a fixed discharge in an open channel. By plotting depth on the X-axis and specific energy on the Y-axis, we can see how energy changes. Each discharge scenario produces a different curve. This graph helps engineers analyze the flow and predict how changes in depth influence the energy available for the flow and allows them to make informed decisions about design.
Examples & Analogies
Think of a graph showing how much energy a cyclist has based on the speed they are traveling uphill. At low speeds, they conserve energy (similar to low flow depth). As they speed up, energy consumption increases, and if they go too fast, it can lead to exhaustion (similar to the hydraulic jump). Graphing these speeds helps them understand the best pace to maintain optimum energy.
Applications of Specific Energy in Design
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The understanding of specific energy aids in the design of efficient canal structures and contributes to the management of urban water systems.
Detailed Explanation
In civil engineering, specific energy concepts are essential for designing open channel systems, like canals and drainage systems. Understanding how to manage energy through the specific energy curve allows engineers to optimize channel designs, ensuring they meet the necessary flow requirements while minimizing energy losses. Effective design improves water management, flood control, and overall efficiency in urban infrastructure.
Examples & Analogies
Consider a city planning its drainage system. They utilize specific energy principles to design the layout ensuring swift water flow during storms while minimizing flooding. This planning is like creating an efficient highway system where quick movement of cars is equated to efficient water flow, avoiding blockages and ensuring everyone reaches their destination on time.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Specific Energy: The sum of potential and kinetic energy per unit weight of fluid.
-
Froude Number: A key ratio that helps define flow regimes in an open channel.
-
Hydraulic Jump: A sudden change in fluid flow, characterized by turbulence, that causes energy losses.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of specific energy can be visualized through a river; as the bed height changes, the flow speed alters, thus affecting the specific energy at various depths.
-
In design scenarios, engineers may refer to specific energy curves to discern how varying flow conditions will affect the energy dynamics in a canal.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the flow of a stream, energy takes its beam; depth's in the flow, speed makes it glow.
📖 Fascinating Stories
-
Imagine a river flowing smoothly over rocks (subcritical) until suddenly it hits a drop leading to a chaotic splash (hydraulic jump). This turbulence represents energy loss in open channel flow.
🧠 Other Memory Gems
-
For Froude, think 'Flow ratio's on the glide, with depth in stride!' (dl = flow velocity / depth).
🎯 Super Acronyms
Remember S.C.S for flow
- S: for subcritical
- C: for critical
- S: for supercritical.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Specific Energy
Definition:
The total mechanical energy per unit weight of fluid relative to a reference datum, consisting of potential and kinetic energy.
-
Term: Froude Number
Definition:
A dimensionless number used to compare inertial and gravitational forces, indicating flow regime in open channel flow.
-
Term: Subcritical Flow
Definition:
Flow condition where Froude number is less than 1, characterized by slower velocities.
-
Term: Supercritical Flow
Definition:
Flow condition where Froude number is greater than 1, characterized by higher velocities.
-
Term: Critical Flow
Definition:
Flow condition where Froude number is equal to 1, at which flow velocity equals wave speed.
-
Term: Hydraulic Jump
Definition:
A sudden transition from supercritical to subcritical flow characterized by turbulence and energy loss.