Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Conservation of Mass
Unlock Audio Lesson
Good morning class! Today, we're exploring the conservation of mass in open channel flow. Can anyone tell me what the conservation of mass implies?
It means that the mass flowing into a system must be equal to the mass flowing out.
Exactly! We can express this with the equation ρv₁y₁ = ρv₂y₂. How does the density factor in here?
If we're assuming incompressible flow, the density stays constant, so it cancels out.
Right! That’s a crucial simplification. Let’s remember this key point—mass inflow equals mass outflow. To reinforce this concept, think of the acronym MIO (Mass Inflow = Outflow).
Can you explain what happens if the flow depth changes?
Of course! As flow depth decreases, velocity increases—this is a fundamental aspect of fluid dynamics. The conservation of mass helps us quantify these changes.
So lower depth means higher velocity, but what about energy?
Great question! We’ll discuss that next. But first, to recap, remember MIO and that as depth decreases, velocity increases.
Conservation of Energy
Unlock Audio Lesson
Now, let’s move on to the conservation of energy in fluid mechanics. The specific energy relates to flow depth and velocity. Who can tell me the formula for specific energy?
Isn’t it E = y + (v^2 / 2g)?
That’s correct! This formula becomes vital when analyzing the effectiveness of our channel designs. Why is the specific energy concept important?
It helps us understand energy loss during flow transitions, right?
Exactly! We'll introduce the concept of hydraulic jumps shortly. To remember the specific energy formula, you can use the saying 'Energy equals depth plus kinetic energy'.
How does this connect with subcritical and supercritical flow?
Excellent connection. Subcritical flow has energy lost to gravity, while supercritical flow is faster, resulting in less energy. Keep this in mind as you calculate energy variations.
Could you summarize the key points about specific energy?
Certainly! Remember the formula: E = y + (v^2 / 2g), understand that it’s critical in evaluating hydraulic jumps and flow behaviors.
Hydraulic Jumps
Unlock Audio Lesson
Let’s delve into hydraulic jumps! A hydraulic jump occurs when supercritical flow transitions to subcritical flow. Can someone summarize the characteristics of these flows?
In supercritical flow, the Froude number is greater than 1, while in subcritical flow, it's less than 1.
Exactly! What happens to energy during this transition?
Energy loss occurs due to turbulence and mixing during the jump.
Correct! This turbulence can be visually stunning. To remember, think of 'Hydraulic Jump = Energy Loss'.
And those jumps can help with mixing air or chemicals in civil engineering, right?
Precisely! Hydraulic jumps serve practical purposes. In summary, these jumps signify transitions between flow types and are integral in designing efficient channels.
Optimal Hydraulic Cross Sections
Unlock Audio Lesson
Finally, let's examine the concept of optimal hydraulic cross-sections. What factors contribute to the design of efficient channels?
The channel's shape, such as rectangular or trapezoidal, affects flow efficiency and energy loss.
Exactly! And we want to achieve the minimum construction cost while maximizing flow capacity. How can we determine these optimal shapes?
We analyze the perimeter and area relationships to maximize hydraulic radius.
Good answer! The best hydraulic sections minimize perimeter for any given flow area. This leads us to more cost-effective designs.
Can you give an example of an optimal cross-section?
Sure, for rectangular channels, this minimizes essentially when the depth is half of the width. Remember: 'Minimum Perimeter = Maximum Capacity'.
Thank you! This concept really ties the whole topic together.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains how the conservation of mass and energy equations are fundamental to analyzing open channel flow, specifically under one-dimensional, incompressible, and steady conditions. It covers flow variations, velocity changes, energy losses, hydraulic jumps, and optimal hydraulic cross-sections for canal structures.
Detailed
Conservation of Mass and Energy Equations
The conservation of mass and energy equations serve as essential tools in fluid mechanics, particularly when analyzing open channel flow. Open channel flow refers to the movement of fluid in a channel where the surface is exposed to the atmosphere, such as rivers, ditches, and canals. This section delves into the foundational equations governing fluid dynamics by simplifying the assumptions to one-dimensional, incompressible, and steady flow conditions.
Key Concepts:
-
Conservation of Mass Equation: In a flowing channel, the mass inflow must equal the mass outflow. Using the density (ρ), velocity (v), and flow depth (y), we express this as:
ρv₁y₁ = ρv₂y₂, where b (channel width) cancels out due to incompressibility. - Conservation of Energy: Specific energy (E) is portrayed through the parameters of flow depth and velocity, allowing the calculation of energy changes during flow transitions.
- Flow Types: The discussion then transitions to subcritical, critical, and supercritical flows, characterized by varying Froude numbers:
- Subcritical Flow: Froude number < 1
- Critical Flow: Froude number = 1
-
Supercritical Flow: Froude number > 1
These conditions dictate flow behavior, turbulence, and energy dissipation. - Hydraulic Jumps: The section also introduces hydraulic jumps, characterized by abrupt changes in flow depth that occur as the flow transitions from supercritical to subcritical, resulting in energy loss and turbulence.
- Optimal Hydraulic Cross-Sections: The final point emphasizes the importance of determining best hydraulic sections for canal design to achieve minimum energy loss, ensuring efficient water transport in civil engineering applications.
Youtube Videos
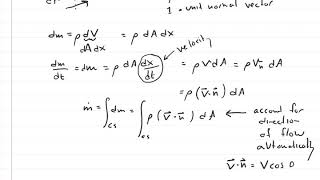
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Basic Concepts of Conservation in Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The basic concept what we use is we will talk about that the conservations of mass and energy equations. So these two equations as we consider for the one-dimensional flow that is what we have simplified it one-dimensional incompressible okay steady flow.
Detailed Explanation
In fluid mechanics, conservation principles are essential for understanding how fluids behave. The conservation of mass states that the mass of the fluid must remain constant over time, while the conservation of energy refers to the principle that energy in a closed system remains constant, though it can change forms. Here, the assumptions simplify our analysis to one-dimensional, incompressible, and steady flow, making it easier to apply these principles and solve fluid flow problems.
Examples & Analogies
Think of a garden hose. When you cover one end of the hose with your thumb, the water still comes out the other end, but at a higher speed. This demonstrates how the mass (amount of water) is conserved, and the energy of the water changes (from pressure energy to kinetic energy) as it travels through the hose.
Force Components in Open Channel Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The flow is governed by the gravity forces and the frictional forces as I discussed earlier. So we have just two force components: the gravity force and frictional force component.
Detailed Explanation
In open channel flow, there are primarily two forces acting on the fluid: gravity and friction. Gravity pulls the water down the slope of the channel, promoting flow, while friction acts against this motion, resisting flow due to contact with the channel's surface. Understanding the interaction between these forces helps predict how the fluid will behave in different conditions within the channel.
Examples & Analogies
Imagine riding a bicycle down a hill. Gravity helps you speed up, while the friction between the tires and the road slows you down. The balance between these forces determines your speed and how far you can go.
Specific Energy in Open Channels
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The same concept we will talk about and more details I will today talk how we can use a specific energy which is a graphical representations of energy versus the flow depth of a channel cross section...
Detailed Explanation
Specific energy in open channel flow refers to the total energy of the flow per unit weight of the fluid, including potential energy due to elevation and kinetic energy due to velocity. Graphically, this is represented as energy plotted against flow depth. This helps in analyzing various flow conditions, such as subcritical and supercritical flow, which correspond to different behaviors of water in the channel.
Examples & Analogies
Think of a water slide. When the water is deep enough (high specific energy), it flows smoothly down the slide (subcritical flow). But if the slide is very steep (supercritical flow), the water moves fast and may become choppy. Understanding how energy changes with depth can help design better slides and channels.
Hydraulic Jump and Energy Losses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When the flow passes through the supercritical to subcritical with a very limited ranges then there are a lot of turbulent structures created...
Detailed Explanation
A hydraulic jump occurs when water transitions from a high-velocity flow (supercritical) to a lower velocity flow (subcritical). This transition results in significant turbulence and energy losses due to the dissipative nature of the jump. It is essential to consider these jumps when designing water channels to understand potential energy losses and ensure efficient flow management.
Examples & Analogies
Imagine a steep water slide that suddenly flattens out. The rushing water hitting a flat section causes splashes and turbulence, showing the energy loss as it slows down. Similarly, a hydraulic jump in a channel acts like that flat section, dissipating energy as water transitions from fast to slow.
Analyzing Hydraulic Jumps with Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I want to draw energy lines or energy gradient line. So how it will come it okay this is y1 depth this will be v1 square by 2g that means this is the locations up to this...
Detailed Explanation
When analyzing hydraulic jumps, engineers use control volumes to account for mass and energy changes. By establishing upstream and downstream conditions, they can calculate energy levels and identify where losses occur. This method allows for a systematic approach to predicting how energy is dissipated across different flow conditions.
Examples & Analogies
Envision a water park wave pool where you watch a wave build up (upstream conditions) and crash down (downstream conditions). By observing the height and speed of the waves at different points, you can determine how energy is transferred and lost in the pool, similar to analyzing flows in hydraulic engineering.
Calculating Energy Losses Due to Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I know the specific energy at upstream specific energy at the downstream just subtracting that I will get the energy losses...
Detailed Explanation
Determining energy losses due to hydraulic jumps involves comparing specific energy levels before and after the jump. By calculating the difference in energy, engineers can quantify how much energy is lost in the jump, aiding in designs that minimize such losses and optimize the flow of water in channels.
Examples & Analogies
Think of filling a balloon with air. If you suddenly let go of it, the air rushes out in all directions. The energy expended in that rush is like the energy lost in a hydraulic jump. Just as you quantify how much air and energy the balloon releases, engineers quantify energy lost in hydraulic jumps to improve channel designs.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Conservation of Mass Equation: In a flowing channel, the mass inflow must equal the mass outflow. Using the density (ρ), velocity (v), and flow depth (y), we express this as:
ρv₁y₁ = ρv₂y₂, where b (channel width) cancels out due to incompressibility. -
Conservation of Energy: Specific energy (E) is portrayed through the parameters of flow depth and velocity, allowing the calculation of energy changes during flow transitions.
-
Flow Types: The discussion then transitions to subcritical, critical, and supercritical flows, characterized by varying Froude numbers:
-
Subcritical Flow: Froude number < 1
-
Critical Flow: Froude number = 1
-
Supercritical Flow: Froude number > 1
-
These conditions dictate flow behavior, turbulence, and energy dissipation.
-
Hydraulic Jumps: The section also introduces hydraulic jumps, characterized by abrupt changes in flow depth that occur as the flow transitions from supercritical to subcritical, resulting in energy loss and turbulence.
-
Optimal Hydraulic Cross-Sections: The final point emphasizes the importance of determining best hydraulic sections for canal design to achieve minimum energy loss, ensuring efficient water transport in civil engineering applications.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In an open channel, if the flow depth reduces, the velocity must increase to conserve mass.
-
When flow converts from supercritical to subcritical flow, energy losses occur, marked by hydraulic jumps.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Mass flow in, mass flow out, in a channel, there’s no doubt.
📖 Fascinating Stories
-
Imagine a river flows steadily; as it narrows, it speeds up, jumps, and stirs the air. This jump causes splash and mix!
🧠 Other Memory Gems
-
Remember MIO (Mass In/Out): Mass inflow equals mass outflow!
🎯 Super Acronyms
SPH (Specific Energy and Hydraulic jumps) to retain the links between these key concepts.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Conservation of Mass
Definition:
A principle stating that mass inflow must equal mass outflow in a fluid system.
-
Term: Conservation of Energy
Definition:
The principle that energy cannot be created or destroyed, only transformed from one form to another.
-
Term: Specific Energy
Definition:
The total mechanical energy per unit weight of fluid, expressed as E = y + (v²/2g).
-
Term: Froude Number
Definition:
A dimensionless number that indicates the flow regime; it is the ratio of the flow velocity to the wave velocity.
-
Term: Hydraulic Jump
Definition:
An abrupt change in flow depth that occurs in open channels, transitioning from supercritical to subcritical flow.
-
Term: Optimal Hydraulic CrossSection
Definition:
The channel shape designed to minimize energy losses and construction costs while maximizing flow efficiency.