Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Specific Energy
Unlock Audio Lesson
Today, let's dive into the concept of specific energy in open channel flow. Can anyone tell me what specific energy comprises?
Is it the total energy per unit weight of fluid?
That's correct! Specific energy is indeed the total energy per unit weight, which combines potential energy from depth and kinetic energy from velocity. Remember the acronym *PEK* for Potential and Kinetic energy.
How do we actually calculate this specific energy?
Great question! The specific energy E is given by the formula: E = y + (v²/2g), where y is the flow depth and v is the velocity. Does anyone remember why we divide the velocity term by 2g?
Because we need to convert velocity to energy units compatible with height?
Exactly! Remember, energy units must match, and that 2g comes from converting velocity to energy per unit weight. Let's summarize what we learned: Specific energy combines height and speed into helpful formulas for designing open channels.
Flow Regimes
Unlock Audio Lesson
Now, let's talk about flow regimes: subcritical, critical, and supercritical flow. Can anyone explain the differences?
Subcritical flow has a Froude number less than 1, while supercritical has a Froude number greater than 1.
Good! And what does the Froude number measure in this context?
It measures the ratio of inertial forces to gravitational forces.
Right on! It helps classify the flow regime. So in subcritical flow, we have higher depths and lower velocities, while the reverse is true for supercritical flow. Can anyone give an example of a situation where one would rely on these classifications?
In designing spillways, where we need to control energy and prevent damage.
Excellent example! These classifications not only affect design but also operational efficiency in civil engineering practices.
Hydraulic Jumps
Unlock Audio Lesson
Next, let's explore hydraulic jumps. Why do you think they are important in open channel flow?
They indicate a transition from supercritical to subcritical flow, right?
Correct! And what happens during that transition?
Energy is lost, resulting in turbulence and sometimes creating noise.
That's right. The turbulence can help in air and chemical mixing, which is beneficial in many applications like wastewater treatment. Remember the term *turbulence can be helpful*! What characteristics can we use to calculate or analyze hydraulic jumps?
The energy equation and flow continuity are crucial here!
Exactly! You will see these concepts tied together in application problems in future classes. Let's summarize: hydraulic jumps are crucial in understanding energy transitions in open channel flows.
Best Hydraulic Cross Sections
Unlock Audio Lesson
Finally, let's discuss the design of the best hydraulic cross sections. What does that involve?
We should optimize the channel shapes to minimize cost and maximize flow capacity.
Exactly! By minimizing the perimeter while maintaining flow area, we achieve more economical designs. What shapes can we consider?
Rectangular, trapezoidal, and even circular!
Great! And what is one important relationship to remember when optimizing these designs?
Hydraulic radius and flow depth! A maximum hydraulic radius gives a maximum velocity.
Right! To wrap up, we learned that efficient channel design can significantly impact infrastructure, so keep these principles in mind when doing practical design work.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore specific energy curves in open channel flow, highlighting the relationships between specific energy, flow depth, and discharge. We also cover hydraulic jumps and best hydraulic cross-sections for effective canal design.
Detailed
Detailed Summary
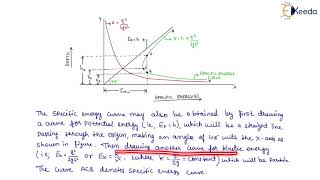
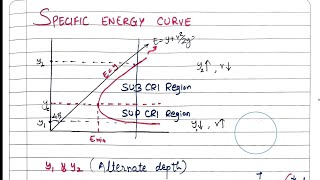
The specific energy curve is a crucial concept in open channel flow, defined as the total energy per unit weight of fluid relative to the channel bottom for a given flow situation. It incorporates the potential energy due to the height of the fluid column and the kinetic energy associated with the fluid's velocity. The relationship between specific energy and flow depth varies based on the flow regime, encompassing subcritical, critical, and supercritical flows.
- Flow Regimes: Understanding the flow regime is essential for predicting flow behavior.
- Subcritical Flow: Froude number < 1 (lower velocity, higher depth)
- Critical Flow: Froude number = 1 (balance between kinetic and potential energy)
- Supercritical Flow: Froude number > 1 (higher velocity, lower depth)
- Hydraulic Jumps: These occur when flow transitions from supercritical to subcritical, leading to energy losses and turbulence.
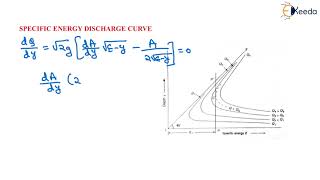
- Applications and Design Implications: The specific energy curve aids engineers in designing hydraulic structures (like sluice gates and spillways) by illustrating how changes in flow depth relate to energy losses and velocity. The best hydraulic cross-sections for specific designs are determined to minimize costs while maintaining efficiency.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Specific Energy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The basic idea to know it, the flow depth variations in open channels, the velocity variations, how the velocity changes it, how much of energy losses, okay. losses is happening it because of the flow and mostly it is governed by the gravity forces and the frictional forces as I discussed earlier. So we have just two force component the gravity force and frictional force component.
Detailed Explanation
In open channel flow, the specific energy curve helps us understand how changes in flow depth and velocity affect energy losses. The main forces at play are gravity, which drives the water flow down the channel, and friction, which resists the flow. The specific energy combines these factors to give insight into the dynamics of water movement in channels.
Examples & Analogies
Imagine a water slide. When you go down the slide (gravity), your speed increases, but if the slide is rough (friction), you might slow down. Similarly, in open channels, the balance between these forces influences how water flows.
Graphical Representation of Specific Energy Curve
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We will talk about and more details I will today talk how we can use a specific energy which is a graphical representations of energy versus the flow depth of a channel cross section where the datum is considered is a channel bottoms more or less the horizontal channel slopes.
Detailed Explanation
The specific energy is represented graphically by a curve that plots energy values against flow depth in a channel. This curve is crucial for engineers, as it visually depicts how energy changes with depth, helping in the design of effective canal structures. The lowest point on this curve corresponds to critical depth, where energy is at a minimum.
Examples & Analogies
Think of a battery gauge showing how much energy a battery has at different levels. The specific energy curve is like that gauge for open channels, allowing engineers to see the 'energy level' of the water flow at various depths.
Supercritical, Subcritical, and Critical Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We can interpret it what is the conditions comes it when you have a subcritical flow. When you throw a stone to a reverse we have a subcritical flow the wave will be propagates the both upstream as well the downstreams. Then we have a very the critical flow which will have a the flow proud number is equal to 1 that is the conditions we have when you have a the critical flow that means the flow proud number is equal to 1.
Detailed Explanation
In open channel flow, the flow can be categorized as supercritical, critical, or subcritical based on the Froude number, which compares the flow velocity to the wave speed. Subcritical flow (F < 1) is slow and allows waves to travel upstream, while critical flow (F = 1) balances speed and depth, representing a pivotal transition. Supercritical flow (F > 1) is fast, with waves unable to travel upstream, leading to different energy dynamics.
Examples & Analogies
Imagine a crowd at a concert. When everyone walks slowly (subcritical), people can easily move in any direction. If everyone moves too fast (supercritical), it's hard to change direction. Critical flow is like when people's movements perfectly align with the music, creating a harmonious flow.
Hydraulic Jump and Energy Losses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When the flow passes through the supercritical to subcritical with a very limited ranges then there are a lot of turbulent structures created okay.
Detailed Explanation
As flow transitions from supercritical to subcritical, it generates a hydraulic jump, causing turbulence and mixing in the water. This jump results in energy losses due to the abrupt change in flow conditions. Engineers must account for these losses when designing water channels and structures, as they impact overall flow efficiency and energy considerations.
Examples & Analogies
Think of a river flowing fast and then hitting a shallow area suddenly. The water splashes and churns, creating turbulence (hydraulic jump) and losing some of its energy. It's like a fast car suddenly hitting a bumpy road, causing it to slow down and shake.
Analyzing Energy Losses in Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I want to draw energy lines or energy gradient line. So how it will come it okay this is y1 depth this will be v1 square by 2g that means this is the locations up to this and I have a let have at this point.
Detailed Explanation
Energy losses can be calculated using energy gradient lines that illustrate how energy decreases across the hydraulic jump. By comparing energy levels before and after the jump, engineers can determine how much energy is lost and how this impacts the flow dynamics.
Examples & Analogies
Imagine a roller coaster. As it reaches the highest point (before the jump), it has maximum potential energy. But as it goes down, some energy is lost to friction and turbulence (akin to the energy loss in a hydraulic jump). Engineers can use this concept to predict how much speed (energy) the coaster will have at the bottom.
Designing for Best Hydraulic Sections
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you look at that minimum the size of systems is a minimum cost of construction.
Detailed Explanation
When designing canals, engineers seek to minimize the construction costs while ensuring efficient water flow. The best hydraulic sections are designed to optimize flow and minimize resistance, which in turn reduces costs associated with the area of construction.
Examples & Analogies
Consider packing for a trip. If you want to carry a lot but minimize the size of your suitcase (cost), you need to plan carefully - choosing the best arrangement for your clothes so they fit efficiently. Similarly, engineers must design channels optimally to handle water flow effectively and economically.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Specific Energy: Defined as the total energy per unit weight of fluid that combines potential and kinetic energy.
-
Froude Number: A dimensionless number that determines flow regimes, crucial for flow classification.
-
Hydraulic Jumps: Transitional phenomena between flow regimes causing energy losses and turbulence.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When designing a spillway, engineers must ensure that the flow remains in the subcritical regime to prevent erosive forces during high discharge.
-
A channel may be designed with a trapezoidal shape to optimize flow performance and minimize maintenance costs by enhancing self-cleaning features.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Between specific energy and flow depth, many relations weave, for channel flows to never deceive.
📖 Fascinating Stories
-
Imagine a river that roars with a jump, suddenly slows down, like a bump! This jump shows energy lost; know it well when designing you're the boss!
🧠 Other Memory Gems
-
PEK: Remember Potential, Energy, Kinetic; for open channels, this foundation is intrinsic.
🎯 Super Acronyms
FES
- Flow
- Energy
- Subcritical - three keys for understanding channel flow essentials.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Specific Energy
Definition:
The total energy per unit weight of fluid relative to the channel bottom, combining potential and kinetic energy.
-
Term: Froude Number
Definition:
A dimensionless number that compares inertial forces to gravitational forces in fluid flow.
-
Term: Hydraulic Jump
Definition:
A phenomenon occurring when flow transitions from supercritical to subcritical, leading to energy losses and turbulence.