Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Hydraulic Jumps and Energy Losses
Unlock Audio Lesson
Good morning class! Today, we'll discuss hydraulic jumps and the energy losses they create. Can anyone tell me what a hydraulic jump is?
Isn't it when the flow changes from supercritical to subcritical?
Exactly! The flow transitions from a high-speed state to a low-speed state, creating turbulence. Let's remember this with the phrase 'Jump from high to low!' What do you think happens to energy during this process?
The energy decreases due to turbulence?
Correct! This decrease in energy is referred to as energy loss, denoted as hL. Can anyone tell me another term related to energy loss?
Specific energy?
Right again! Specific energy is the total mechanical energy per unit weight of the fluid. Let’s summarize: Hydraulic jumps result in energy loss due to turbulence when transitioning from supercritical to subcritical flow.
Froude Number and Flow Classification
Unlock Audio Lesson
Now, let's dive into Froude numbers. Who can explain what the Froude number indicates?
It’s the ratio of flow velocity to the speed of surface waves.
Exactly! It helps determine flow types: F < 1 is subcritical, F = 1 is critical, and F > 1 is supercritical. Here's a mnemonic to remember this: 'Sub, Critical, Super - that's the flow order!' Can anyone give an example of a situation you might find supercritical flow?
When water flows quickly over a spillway.
Right! In that case, we would expect a hydraulic jump downstream when it transitions to subcritical flow. So, always remember to calculate Froude numbers to assess flow conditions.
Energy Loss Calculations
Unlock Audio Lesson
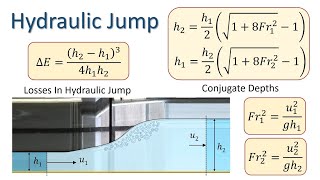
Let’s now look at how we can calculate energy losses due to hydraulic jumps. We can use specific energy values before and after the jump to find the energy loss, hL.
So we just subtract the downstream specific energy from the upstream specific energy?
Exactly! You can find hL using the formula: E1 = E2 + hL. It's a direct way to quantify losses. Can anyone recall what factors could affect these energy losses?
Turbulence and flow velocity?
Good observation! Higher turbulence usually leads to greater energy loss. Therefore, understanding how to calculate and minimize these losses is vital for canal design.
Practical Applications in Engineering
Unlock Audio Lesson
Finally, let's discuss the practical applications. Why do you think it's important for civil engineers to understand hydraulic jumps?
To design efficient structures like canals or spillways.
Exactly! Effective designs minimize energy losses and maintain desired flow conditions. What can happen if we don't plan for these hydraulic jumps?
There could be flooding or erosion issues.
Correct! Engineers must account for these jumps. The importance of hydraulic jumps goes beyond just calculations; it’s crucial for sustainable engineering practices.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section highlights the principles of fluid mechanics as they pertain to hydraulic jumps, covering topics like energy conservation, the relationship between subcritical and supercritical flows, and relevant equations. It emphasizes the importance of controlling energy losses in canal designs and the role of hydraulic jumps in engineering applications.
Detailed
Energy Losses Associated with Hydraulic Jumps
This section delves into the phenomenon of hydraulic jumps, which occur when there is a transition from supercritical (high speed) to subcritical (low speed) flow in open channels. It begins with the foundational principles of fluid mechanics, specifically focusing on the conservation of mass and energy equations for one-dimensional, incompressible, and steady flows. The section explains the significance of Froude numbers in identifying flow conditions, categorizing flows as subcritical (F < 1), critical (F = 1), or supercritical (F > 1).
The discussion points out how energy losses are primarily caused by turbulence during hydraulic jumps, leading to a loss of total mechanical energy. Graphical representations of specific energy versus flow depth are introduced, allowing readers to visualize these transitions and associated energy losses (hL).
Finally, it emphasizes the importance of understanding hydraulic jumps for the effective design of civil engineering structures such as canals and spillways, aiming for optimized flow conditions and minimized energy losses.
Youtube Videos
![Open Channel Flow 38 - {How to calculate sequent depth and energy loss in hydraulic jump problem]](https://img.youtube.com/vi/eAjApbk4NhA/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When the flow passes through the supercritical to subcritical regions with a limited range, turbulent structures are created, which is called a hydraulic jump. Energy losses occur during this transition.
Detailed Explanation
A hydraulic jump occurs when a fast-moving flow (supercritical flow) slows down as it transitions to a slower flow (subcritical flow). This transition is accompanied by turbulence, which is the chaotic mixing of fluid particles. Energy is lost during this process due to various factors like turbulence and momentum change.
Examples & Analogies
Imagine a child sliding down a smooth slide (supercritical flow) and reaching a flat area (subcritical flow) at the bottom. As the child slows down and moves on the flat surface, they might bump into other kids or play around, representing the turbulence. The energy from the slide (initial kinetic energy) is lost as they engage with other children and the ground.
Conditions of Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Supercritical flow occurs when the Froude number is greater than 1. Conversely, subcritical flow has a Froude number less than 1. The transition between these two states marks the hydraulic jump.
Detailed Explanation
The Froude number is a dimensionless value that helps determine the type of flow. When the Froude number is greater than 1, the flow is considered supercritical, indicating high speed and low depth. A Froude number less than 1 indicates subcritical flow, characterized by lower speed and higher depth. The hydraulic jump signifies the transition between these two flow regimes.
Examples & Analogies
Think of a river flowing rapidly over rocks (supercritical flow) until it cascades into a tranquil pool (subcritical flow). The rapid water hits the calm surface, creating splashes (hydraulic jump), symbolizing the turbulence and energy loss occurring in the process.
Energy Losses During Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Energy losses occur as the flow transitions from supercritical to subcritical, with a notable reduction in flow energy. This energy loss is represented as 'hL' and can be calculated from specific energy values upstream and downstream.
Detailed Explanation
During a hydraulic jump, the kinetic energy of the water flow is converted into turbulent energy, resulting in a loss of energy represented by 'hL'. This loss can be calculated by determining the specific energy at both upstream and downstream points and finding the difference. For engineers, this energy loss helps design structures that efficiently manage flow energy.
Examples & Analogies
Consider standing under a waterfall while holding a bucket. As the water falls rapidly (supercritical flow), it splashes everywhere when it hits the pool below (hydraulic jump), wasting much of its energy as it turns into frothy turbulence. The energy that could have pushed the water forward is lost as splashes and turbulence.
Calculation of Energy Losses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To analyze hydraulic jumps effectively, one needs to calculate the specific energy upstream (E1) and downstream (E2) of the jump. The energy loss can then be calculated as 'E1 - E2'.
Detailed Explanation
Analysts and engineers can evaluate energy dissipation by calculating the specific energies at the two respective points of the hydraulic jump (upstream and downstream). The difference between these energies quantifies the energy loss (hL), crucial for designing efficient hydraulic systems and evaluating the performance of existing ones.
Examples & Analogies
Think of a water balloon thrown from a height (upstream) bursting when it hits the ground (downstream). The energy of the balloon before it hits the ground represents E1, and the splatter on the ground represents the energy dissipated (E2). The amount of energy lost in this process correlates to calculations used in hydraulic jumps.
Significance of Energy Losses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Hydraulic jumps are not only crucial for understanding energy losses but are also significant in engineering design to promote mixing and ensure effective chemical distributions in waterways.
Detailed Explanation
Understanding hydraulic jumps is essential for engineers because they play a role in mixing different components in water (such as air or chemicals) effectively. Proper design that takes into account energy losses helps ensure functionality and efficiency in channel flow systems and treatment processes.
Examples & Analogies
Imagine a chef mixing ingredients in a bowl, where the energetic action of stirring thoroughly blends everything together. Similarly, in a hydraulic jump, the turbulent mix ensures that any harmful substances in the water get distributed evenly, making it safer for downstream ecosystems.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic Jumps: Sudden transitions in flow that lead to energy loss.
-
Froude Number: A critical value for identifying flow conditions.
-
Energy Loss (hL): The difference in energy between upstream and downstream flows.
-
Specific Energy: A measure of total mechanical energy per unit weight.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of hydraulic jump observed in a spillway where water flows quickly into a stilling basin, leading to turbulence and energy dissipation.
-
Real-life application concerning bridge design where engineers account for hydraulic jumps to avoid upstream flooding.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Jump from fast to slow, energy loss is what you know.
📖 Fascinating Stories
-
Imagine a stream rushing over stones, suddenly hitting a pool that slows it down, creating splashes—this is the hydraulic jump in action.
🧠 Other Memory Gems
-
Froude's Formula: 'Velocity Over Wave Spelled Saves' to remember v/sqrt(g*y).
🎯 Super Acronyms
H.E.A.V.E. (Hydraulic Energy And Velocity Erosion) helps recall the relationship between hydraulic jumps and energy losses.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Jump
Definition:
A sudden change in flow conditions from supercritical to subcritical flow characterized by turbulence and energy loss.
-
Term: Froude Number
Definition:
A dimensionless number used to classify flow regimes in open channels based on the ratio of the flow velocity to the wave speed.
-
Term: Specific Energy
Definition:
The total mechanical energy per unit weight of fluid, commonly expressed as the sum of potential and kinetic energy.
-
Term: Energy Loss (hL)
Definition:
The difference in specific energy between the upstream and downstream sections of a hydraulic jump.
-
Term: Subcritical Flow
Definition:
Flow characterized by a Froude number less than one; it is slow and tranquil.
-
Term: Supercritical Flow
Definition:
Flow characterized by a Froude number greater than one; it is rapid and generally turbulent.