Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mass Conservation in Open Channel Flow
Unlock Audio Lesson
Good morning, everyone! Today, we're going to discuss mass conservation equations and their critical role in analyzing open channel flow. Can anyone remind me what mass conservation means?
It means that the mass of fluid entering a system equals the mass leaving the system.
Exactly! Now, in fluid mechanics, we focus primarily on incompressible flow. So, if we denote the inflow as m_in and the outflow as m_out, we can write: m_in = m_out. Hence, what do you think will happen to the velocity with respect to flow depth?
If the flow depth decreases, the velocity should increase.
Correct! This leads us to our mass conservation formula: v1 * y1 = v2 * y2. The change in height affects the velocity due to the predefined flow rate.
I see! That’s how we can calculate the flow at different points!
Exactly, and by applying these principles, we can analyze various scenarios in open channel flow efficiently.
To summarize, mass conservation is about balancing the inflow and outflow of fluid, which can predict changes in velocity with changes in depth.
Hydraulic Jumps and Flow regimes
Unlock Audio Lesson
Now, who can tell me about hydraulic jumps and why they are significant?
Hydraulic jumps occur when the flow changes from supercritical to subcritical, creating turbulence.
Yes, that’s right! And what are the Froude number conditions for subcritical, critical, and supercritical flows?
For subcritical flow, it's less than 1; critical flow is equal to 1, and supercritical flow is greater than 1.
Perfect! The transition between these flows is critical in designing hydraulic structures, particularly to manage energy dissipation effectively. Can you think of where we might see hydraulic jumps in real life?
In spillways or during the flow over dams!
Exactly! Understanding these phenomena allows us to design systems that effectively manage water flow while minimizing energy loss.
To summarize, hydraulic jumps play a significant role in channel design by demonstrating the transition between different flow types, emphasizing the importance of energy management in civil engineering.
Specific Energy Curve
Unlock Audio Lesson
Let’s now explore specific energy and its graphical representation. Why do we concern ourselves with specific energy in open channel flow?
It helps us understand how energy varies with flow depth and helps in optimizing channel design.
Exactly! The curve can illustrate how specific energy changes with varying depths. What do common shapes of this curve look like?
I think it would be a parabola, ensuring minimum energy at critical depth.
Right! As flow conditions change due to factors like discharge, we observe different specific energy levels. By knowing how to draw and interpret this curve, how can we apply this in practical terms?
It can help engineers determine optimal widths and depths for channels!
Absolutely! The specific energy curve is crucial for understanding flow characteristics in channel design.
To conclude, the specific energy curve is essential as it provides insights into flow behavior and energy relationships, aiding engineers in designing efficient hydraulic structures.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the principles of mass conservation and energy equations and their significance in analyzing open channel flows, particularly in the context of hydraulic jumps and the implications for canal design.
Detailed
Mass Conservation Equations in Open Channel Flow
In fluid mechanics, particularly concerning open channel flow, the mass conservation and energy equations form the foundational principles guiding the analysis and design of hydraulic structures. When examining one-dimensional, incompressible, and steady flow, these equations simplify the understanding of how fluid behaves under varying depth and velocity conditions. The principles of specific energy, critical depth, and hydraulic jumps are essential in predicting how flow will change with different geometrical and hydraulic conditions.
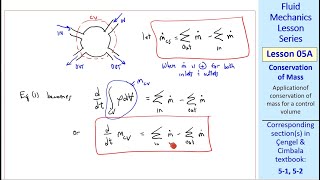
One key concept is the relationship derived from the mass conservation equation, stating that the mass inflow equals the mass outflow in a steady-state scenario. This can be algebraically expressed as:
Where v1 and v2 are the flow velocities and y1 and y2 are the respective flow depths. If the depth decreases (e.g., due to a sluice gate being lowered), then the velocity increases as per the continuity equation.
The section emphasizes the importance of recognizing flow regimes such as subcritical (Froude number < 1), critical (Froude number = 1), and supercritical flow (Froude number > 1) and discusses the implications of each regime, including the occurrence of hydraulic jumps. Hydraulic jumps are remarkable phenomena where the flow transitions from supercritical to subcritical, accompanied by turbulence and energy dissipation. Understanding these principles helps engineers determine the design of hydraulic structures to optimize flow control and efficiency.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Mass Conservation in Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The basic concept what we use is we will talk about that the conservations of mass and energy equations. So these two equations as we consider for the one-dimensional flow that is what we have simplified it one-dimensional incompressible okay steady flow.
Detailed Explanation
Mass conservation in fluid mechanics states that the amount of mass flowing into a system must equal the mass flowing out, provided there are no accumulations within the system. This principle is particularly applicable to one-dimensional, incompressible, and steady flows where the velocity and density remain constant across the section. In simpler terms, if you envision a pipe through which water is flowing, the volume of water entering one end must equal the volume exiting the other end, assuming no leaks or accumulation happens inside the pipe.
Examples & Analogies
Imagine you have a garden hose connected to a water supply. When you turn on the tap, water begins to flow through the hose. If you close the end of the hose, the water accumulates inside, but as long as the end is open, the amount of water flowing in is equal to the amount flowing out. This is similar to the concept of mass conservation.
Concept of Velocity and Depth in Open Channel Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What do you mean by that as the depth decreases the velocity is going to increase it okay. That is what a very simple way we can understand it if the depth of the flow is decreases then the velocity increases.
Detailed Explanation
In open channel flow, there is an inverse relationship between the depth of the flow and its velocity. This means that as the depth of the water decreases (for instance, when a sluice gate is lowered), the water speeds up. This principle is crucial in understanding various hydraulic phenomena and is essential for designing channels to handle different flow conditions. The relationship can be attributed to the conservation of mass: if the area through which water flows decreases, the speed must increase to keep the mass flow rate constant.
Examples & Analogies
Think of a funnel. When you pour liquid in at the top, it moves slowly at first because the diameter is wide. But as the liquid reaches the small end of the funnel, it speeds up. This is akin to how water behaves in an open channel when its depth reduces.
Hydraulic Jump and Energy Losses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Supercritical is to subcritical reasons it creates a jump you can see that is a jump a jump behavior this is the jump we call a hydraulic jump and these the hydraulic jump create a lot of turbulent structures.
Detailed Explanation
A hydraulic jump occurs when water flows from a high-velocity low-depth (supercritical) state to a lower velocity higher-depth (subcritical) state. This transition creates turbulence, and the energy lost during this process leads to a jump in the water surface. It’s essential in engineering design since hydraulic jumps can cause significant energy losses, which must be accounted for in hydraulic systems. Understanding their formation helps in designing channels and structures like spillways effectively.
Examples & Analogies
Consider a waterfall. As water cascades over the edge, it falls quickly (supercritical flow). When it hits the pool at the bottom, it suddenly spreads out and slows down (subcritical flow), creating splashes and turbulence—this visual phenomenon is similar to a hydraulic jump.
Energy Losses and Specific Energy Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I want to draw energy lines or energy gradient line. So how it will come it okay this is y1 depth this will be v1 square by 2g that means this is the locations up to this and I have a let have at this point.
Detailed Explanation
The energy lines in fluid mechanics help visualize the energy at different points in a flow. The energy at any point can be represented as a sum of the potential energy and kinetic energy of the fluid. The energy gradient line shows how energy changes along the flow path, revealing how energy losses (like those occurring through hydraulic jumps) occur. Understanding this helps in analyzing the efficiency and performance of fluid systems.
Examples & Analogies
Imagine a roller coaster track. The height of the track represents potential energy, and as the coaster goes down, the speed increases, representing kinetic energy. If there’s a sudden drop or a turn, energy is lost in the form of sound and heat, similar to how energy losses occur in hydraulic systems.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Conservation: The principle that mass must be conserved in a fluid system, leading to the equation v1 * y1 = v2 * y2.
-
Hydraulic Jump: The transition from supercritical flow to subcritical flow characterized by turbulence and energy loss.
-
Specific Energy: Defined as potential energy plus kinetic energy in fluid flow; critical for understanding channel behavior.
-
Froude Number: A dimensionless ratio used to describe flow behavior, guiding engineers in assessing flow regimes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating flow velocity changes when the channel depth increases or decreases, showcasing how mass conservation principles apply in practice.
-
Identifying hydraulic jump locations in spillways and waterfalls, crucial for ensuring water management and safety.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When flow’s too fast, a jump you’ll see; it slows down for stability.
📖 Fascinating Stories
-
Imagine a fast river rushing over rocks, hitting a wall, and jumping up, splashing water all around—a hydraulic jump in action!
🧠 Other Memory Gems
-
Remember 'FSUC' for Froude Number: Flow < 1 is Subcritical, Flow = 1 is Critical, Flow > 1 is Supercritical.
🎯 Super Acronyms
JUMP for remembering Hydraulic Jump
- 'Jolt Upstream
- Mass drops
- Pressure loss.'
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Jump
Definition:
A rapid transition between supercritical and subcritical flow, creating turbulence and energy loss.
-
Term: Froude Number
Definition:
A dimensionless number comparing inertial and gravitational forces in a flow, used to determine the flow regime.
-
Term: Specific Energy
Definition:
The total energy per unit weight of fluid flow, defined as the height of the flow plus the velocity head.
-
Term: Continuity Equation
Definition:
A mathematical statement that the mass flow rate must remain constant from one cross-section of a channel to another.