Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydraulic Jumps
Unlock Audio Lesson
Good morning, class! Today we're diving into the fascinating world of hydraulic jumps. Can anyone tell me what happens during a hydraulic jump?
Isn’t it when the water changes from fast-moving to slower-moving flow?
Exactly! Hydraulic jumps occur when the flow transitions from supercritical to subcritical states. Can anyone recall what defines supercritical flow?
When the Froude number is greater than one!
Correct! And remember, a Froude number less than one indicates subcritical flow. It's essential to understand these concepts as they underpin the behavior of hydraulic jumps.
Now, let's visualize this. Think of a slope with fast-moving water, and suddenly it hits a drop. What do you think happens?
It creates turbulence and a splash. Is that the jump?
Well put! The splash and turbulence indicate energy loss, which is a key feature of hydraulic jumps.
To summarize today’s session: Hydraulic jumps transition flow from supercritical to subcritical, characterized by energy loss and turbulence. Remember Froude numbers are essential in defining these states.
Energy Loss Calculation
Unlock Audio Lesson
Now that we understand what hydraulic jumps are, let's look at how we can calculate energy losses. Can anyone share a formula related to specific energy?
Isn’t it E = y + (v^2)/(2g)?
Yes! And how can we use this to determine energy loss during a jump?
We can compare the specific energy before and after the jump.
Exactly! The energy loss can be calculated as the difference between the initial and final specific energy, often represented as hL. Who can express this mathematically?
E1 = E2 + hL?
Well done! So, understanding specific energy allows us to quantify the energy losses associated with hydraulic jumps.
In summary, energy loss during hydraulic jumps is calculated by comparing specific energies. This understanding is crucial for designing efficient hydraulic systems.
Practical Applications
Unlock Audio Lesson
Let's discuss the practical implications of our learning. Why are hydraulic jumps significant in engineering, say, in designing spillways?
They help control floodwaters, right?
Absolutely! Hydraulic jumps dissipate energy, which is critical to prevent erosion downstream. What might happen if we didn't account for jumps in our designs?
There could be flooding or damage to structures!
Right! That's why hydraulic engineers need to incorporate these phenomena into their designs. Can anyone think of examples where you might observe hydraulic jumps in real life?
At spillways or dam releases!
Exactly! They're visually striking during heavy rains. In conclusion, understanding hydraulic jumps not only aids in calculations but is essential for practical engineering solutions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section highlights the principles of hydraulic jumps occurring as flow transitions from supercritical to subcritical conditions, exploring energy loss and the significance of specific energy in analyzing flow characteristics.
Detailed
Detailed Summary
In hydraulic engineering, understanding the behavior of open channel flow is crucial, particularly the concept of hydraulic jumps, which occur when flowing water transitions from supercritical to subcritical states. This phenomenon is characterized by a sudden change in flow depth and velocity, resulting in turbulence and energy loss. The flow dynamics are governed by the conservation of mass and energy, where the relationship between upstream and downstream velocities and depths can be quantified using Froude numbers. A Froude number greater than one indicates supercritical flow, while a number less than one indicates subcritical flow. The section elaborates on the calculations involved in estimating energy losses during these jumps, incorporating specific energy curves and the significance of critical depth in designing canal structures. Additionally, it discusses the engineering implications of hydraulic jumps in practical applications such as spillways and drainage systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
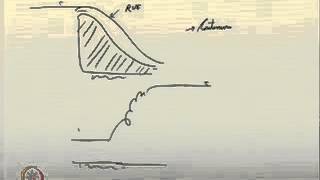
Let us come back to the hydraulic jumps, how does it form? If you look at it, if you have more or less a horizontal surface and you have a sluice gate. The flow is coming from this side, it has a depth. After that, you can see that the flow will be like a jet flow.
Detailed Explanation
A hydraulic jump occurs when water flowing in an open channel transitions from a supercritical state (high speed) to a subcritical state (lower speed). This often happens downstream of a sluice gate where the water initially flows rapidly like a jet due to a sudden change in channel depth or slope. The transition leads to significant turbulence and a sudden increase in flow depth.
Examples & Analogies
Think of a water fountain where the water shoots high into the air (supercritical flow) before it falls back into a pool below (subcritical flow). The moment it hits the water pool, you observe splashes and turbulence, resembling a hydraulic jump.
Conditions of Flow and Conservation of Mass
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we can see that typically it will have a jet type of flow... if this is the v1 velocity and this is the v2 velocity... So we have a v1 y1 is equal to v2 y2.
Detailed Explanation
In this scenario, the mass conservation principle applies, meaning the mass inflow must equal the mass outflow. For incompressible flows, this translates to the relationship that the product of the velocity and the depth of flow at two different points must be the same. Therefore, v1 times y1 (upstream flow) equals v2 times y2 (downstream flow) which helps us understand how velocity and depth are interrelated.
Examples & Analogies
Imagine a garden hose: when you partially cover the opening with your thumb, the water shoots out faster (higher velocity) and the hose's opening area decreases (similar to the depth of flow). Here, the volume of water being pushed remains constant, but its speed changes, illustrating the same principle.
Formation of Hydraulic Jump
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As the velocity increases, does it go to supercritical levels or not? ... the flow is changing from supercritical to subcritical regions.
Detailed Explanation
As water transitions from supercritical flow (flow with a Froude number greater than 1) to subcritical flow (Froude number less than 1), a hydraulic jump forms. This transition is characterized by a rapid change in flow depth and velocity, often accompanied by turbulent mixing and energy dissipation, leading to a jump in the water surface.
Examples & Analogies
Picture throwing a rock into a still pond: the splash created when it hits the water is akin to a hydraulic jump. The rock (representing supercritical flow) hits the water's surface, causing a turbulence (hydraulic jump) that spreads outward.
Effects of Hydraulic Jump
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Hydraulic jumps create a lot of turbulent structures... energy losses happen when flow transitions from supercritical to subcritical.
Detailed Explanation
When a hydraulic jump occurs, significant energy loss results, primarily because of turbulence created in the water. This means that the energy that was previously used to maintain a high-speed flow is dissipated during the transition, which can be a critical factor in designing channels and structures downstream.
Examples & Analogies
Think of a roller coaster: when you go over a high peak and down into a dip, you rapidly lose speed due to the energy required to go back up. Similarly, water loses energy as it transitions from a high-speed flow to a slower, deeper flow, resulting in turbulence—much like the splashing of water at the bottom of the roller coaster dip.
Analyze Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I know the upstream conditions... we can compute the energy losses... E1 is equal to E2 plus hL.
Detailed Explanation
To analyze hydraulic jumps, we can use conservation of energy principles along with previously discussed relationships involving flow depth and velocity. By knowing the flow conditions upstream (E1) and downstream (E2), we can calculate the energy losses (hL) that occur during the jump. This is essential for designing effective hydraulic structures.
Examples & Analogies
This analysis is like budgeting—if you know how much money you have at the start (E1) and how much you need to spend (E2), you can determine how much you are losing (hL) during your expenditures to effectively plan for your finances.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic Jump: A transition in flow from supercritical to subcritical, characterized by energy loss.
-
Froude Number: A dimensionless value representing the flow regime; greater than 1 indicates supercritical flow.
-
Specific Energy: The total energy per unit weight of fluid, key in evaluating flow conditions.
-
Energy Loss: The difference in energy before and after a hydraulic jump, significant for system design.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When a river flows over a steep drop, the water accelerates and then suddenly slows down at the bottom, creating a hydraulic jump.
-
In spillway design, engineers plan for hydraulic jumps to manage and dissipate energy effectively, preventing downstream erosion.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When water jumps high and makes a splash, a hydraulic jump causes flows to clash.
📖 Fascinating Stories
-
Imagine a river running swiftly over a cliff. As it hits the bottom, it crashes into turbulent waters, showcasing the energy loss during a hydraulic jump.
🧠 Other Memory Gems
-
JUMP: Just Understand Motion's Power! (Referencing the energy dynamics of jumps)
🎯 Super Acronyms
H.E.A.V.Y
- Hydraulic Energy At Various Yields (Remembering energy losses in jumps)
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Jump
Definition:
A phenomenon in open channel flow where fluid transitions from supercritical to subcritical flow, resulting in turbulence and energy loss.
-
Term: Froude Number
Definition:
A dimensionless number that compares inertial and gravitational forces in fluid flow, used to determine flow regimes.
-
Term: Specific Energy
Definition:
The total energy per unit weight of fluid, consisting of the potential energy and kinetic energy components.
-
Term: Energy Loss (hL)
Definition:
The difference in specific energy between upstream and downstream points in a hydraulic system due to inefficiencies and turbulence.