Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Specific Energy
Unlock Audio Lesson
Today, we're diving deep into specific energy, a critical concept in open channel flow. Can anyone tell me what specific energy means?
Is it the total energy of the flow per unit weight of fluid?
Exactly! Specific energy is composed of the flow depth and velocity head. We represent it graphically to observe how changes in flow depth can affect energy levels. Can anyone summarize the three different flow conditions?
There are subcritical, critical, and supercritical flows.
Great! Remember, the Froude number helps define these conditions. Let’s use the acronym FCS for Flow Conditions: F for Froude, C for Critical, and S for Sub/Supercritical.
Critical Flow and Froude Number
Unlock Audio Lesson
Now that we understand specific energy, let’s discuss the Froude number. Who can tell me its relationship with flow types?
The Froude number is a dimensionless number calculated as the flow velocity divided by the square root of gravitational acceleration times the flow depth.
Nice job! And what does a Froude number of 1 indicate?
It indicates critical flow where gravitational and inertial forces are balanced.
Correct! Remember: Critical flow implies the flow velocity equals the speed of surface waves, which brings us to our next concept.
Hydraulic Jumps
Unlock Audio Lesson
Let’s talk about hydraulic jumps. Who can explain what happens during a hydraulic jump?
It occurs when the flow moves from supercritical to subcritical, resulting in energy losses.
Exactly! The energy losses can have significant implications for hydraulic structure design. What can we observe when hydraulic jumps occur?
We usually see turbulence and mixing, which are important for certain engineering applications.
Very accurate! Remember that visualizing these jumps can help engineers design better structures. Let's summarize with the mnemonic JUMP - J for Jump, U for Upstream to Downstream transition, M for Mixing, P for Pressure energy loss.
Designing Canal Structures
Unlock Audio Lesson
Now that we’ve covered energy and hydraulic jumps, let's discuss the best hydraulic cross-sections for canals. Who can share some standard shapes we might consider?
We have rectangular, trapezoidal, and circular shapes.
Excellent! What factors do we consider when selecting a cross-section?
We need to think about minimizing construction costs while maximizing flow efficiency.
Exactly! A well-designed canal should reflect economic considerations and flow dynamics. Let’s remember this with the acronym COST: C for Cost-effective, O for Optimal design, S for Shape, T for Turbulence management.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section provides a thorough explanation of specific energy in open channel flow, discussing fundamental concepts such as the conservation of mass and energy, the definition of specific energy and critical flow conditions, hydraulic jumps, and various hydraulic cross sections for effective canal design.
Detailed
Detailed Summary
In this section, the concept of specific energy in open channel flow is explored, focusing on key principles that govern this area of fluid mechanics. Specific energy is defined as the total energy of the flow per unit weight of fluid. It comprises the flow depth and velocity head, presented graphically to illustrate how variations in flow depth affect energy levels. The section introduces the critical flow condition, characterized by a Froude number equal to one, which signifies a balance between gravitational and inertial forces in the flow.
Furthermore, it discusses the implications of flow regimes: subcritical flow (Froude number < 1), critical flow (Froude number = 1), and supercritical flow (Froude number > 1). The phenomenon of hydraulic jumps, specifically the transition from supercritical to subcritical flows, is highlighted, explaining how energy losses occur during this transition and the repercussions for engineering design in hydraulic structures. The segment wraps up with insights on optimal hydraulic cross sections, emphasizing practical aspects of canal design, which aim to minimize construction costs while ensuring efficient flow conveyance.
Youtube Videos
![Open Channel Flow - 23 [Concept of Specific energy, conditions of critical flow, Froude number]](https://img.youtube.com/vi/rzVDDrE9UpU/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Specific Energy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The basic idea to know it, the flow depth variations in open channels, the velocity variations, how the velocity changes it, how much of energy losses, okay. losses is happening it because of the flow and mostly it is governed by the gravity forces and the frictional forces.
Detailed Explanation
This section introduces the concept of specific energy, which is essential for understanding flow in open channels. It discusses how flow depth and velocity vary in these channels and emphasizes that energy losses occur primarily due to gravity and friction forces. Understanding these concepts is crucial for accurately designing and analyzing open channel systems.
Examples & Analogies
Think of flowing water in a river. When the water flows over rocks or bends, it slows down (increased friction) and may rise higher in some places (increased depth). This change represents energy lost in the flow due to gravity and friction, much like how a car slows down when driving uphill or on a rough road.
Understanding Subcritical, Critical, and Supercritical Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Subcritical flow means when you have a flow Froude number lesser than 1... Then we have critical flow which will have a the flow proud number is equal to 1... This is what is a recap what we discussed in the last 2 classes.
Detailed Explanation
This part explains the classification of flows based on the Froude number: subcritical (F < 1), critical (F = 1), and supercritical (F > 1). Each type reflects different characteristics of flow behavior, influencing design parameters in engineering applications. Recognizing these types helps in understanding the flow's energy dynamics.
Examples & Analogies
Imagine watching a river. In areas where the water flows gently, it's like subcritical flow—calm and stable. When you see a spot where water begins to whip and surge faster, that's akin to supercritical flow, where energy and velocity increase, much like a sprinter kicking into high gear during a race.
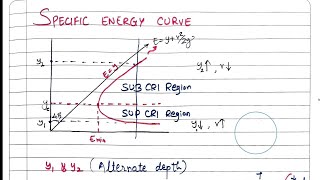
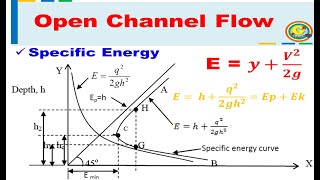
Specific Energy Curve Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We can use a specific energy concept that is to understand how the flow variations will be there...specific energy curve and hydraulic jump.
Detailed Explanation
Here, the specific energy concept is illustrated graphically, displaying specific energy versus flow depth for channel cross sections. It serves as an analytical tool to understand how variations in depth affect specific energy, particularly during phenomena like hydraulic jumps.
Examples & Analogies
Consider how a water slide works. At the top of the slide, the water has plenty of energy (much like high specific energy) due to height. As it slides down, the energy converts into speed (velocity), illustrating how energy changes with height and flow depth, akin to the specific energy concept.
Velocity and Flow Changes in Open Channels
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What do you mean by that as the depth decreases the velocity is going to increase it okay... but mostly if you come to this you can have this subcritical flow you can have a supercritical flow.
Detailed Explanation
This section clarifies the relationship between flow depth and velocity. As the depth of water in an open channel decreases, the velocity tends to increase, which has significant implications for calculating flow rates and designing hydraulic systems. Understanding this concept is crucial for predicting how flow behaves under different conditions.
Examples & Analogies
Imagine squeezing a garden hose. When you cover part of the opening with your thumb (reducing the depth of flow), the water speeds up as it exits, similar to how in open channels, a decrease in depth leads to an increase in flow velocity. This principle is key in both gardening and engineering.
Hydraulic Jump Explanation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When the flow passes through the supercritical to subcritical with a very limited ranges then there are a lot of turbulent structures created okay...
Detailed Explanation
This chunk discusses hydraulic jumps, which occur when water transitions from supercritical flow to subcritical flow. This transition results in turbulence and energy losses due to significant changes in velocity and depth. Understanding hydraulic jumps is essential for engineers to manage potential energy losses in hydraulic designs and structures.
Examples & Analogies
Visualize water flowing swiftly over a waterfall. As it crashes down, it becomes turbulent due to the sudden change in speed and depth, creating a 'jump' effect. This jump highlights how fast-moving water can change when it meets obstacles or shallower areas, similar to how hydraulic jumps behave in engineering scenarios.
Energy Losses During Hydraulic Jump
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I want to draw energy lines or energy gradient line... E1 is equal to E2 plus hL a very simple thing.
Detailed Explanation
In this part, the concept of energy losses during hydraulic jumps is presented using energy gradients. It establishes the relationship between upstream and downstream energy states, highlighting that energy drops occur due to turbulence and other factors during the jump, which is essential for assessing performance in hydraulic systems.
Examples & Analogies
Think about when you fill a bucket of water. If you turn the faucet on too high, the water splashes everywhere, wasting energy instead of just filling the bucket peacefully. The energy lost in spills resembles how energy losses occur during hydraulic jumps, where the water's energy is not effectively using for forward flow anymore.
Analyzing Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you look at the problems what we are talking about we can always look at that how the things are happening it at this point okay...
Detailed Explanation
This section focuses on the method of analyzing hydraulic jumps using control volumes and mass conservation principles. By applying these principles, engineers can determine flow characteristics before and after a hydraulic jump, which is important for evaluating system efficiency and safety.
Examples & Analogies
Consider a water park with a lazy river. As the water moves through interconnected areas (control volumes), engineers can predict how changes in depth or barriers will affect the speed and flow of water, just as they do with hydraulic jumps in rivers or channels.
Computing Energy Losses and Specific Energy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
How to get the v2 and y2 because upstream conditions we know it v1 y1 flow proud numbers the specific energy...
Detailed Explanation
In this chunk, more techniques are provided for calculating downstream flow velocity (v2) and depth (y2) from known upstream conditions (v1, y1). By employing mass conservation equations and energy methods, one can estimate energy losses and downstream characteristics. This is fundamental for engineers to optimize hydraulic designs.
Examples & Analogies
Imagine you are baking a cake. You know how much batter you have, and you want to determine the size of the cake once baked (downstream conditions). By using your initial batter's quantity and the baking time (upstream conditions), you can predict the cake's dimensions, similar to calculating flow characteristics.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Specific Energy: Total energy per unit weight of fluid in open channels.
-
Froude Number: Dimensionless ratio of inertial to gravitational forces in fluid.
-
Hydraulic Jump: Energy dissipative phenomenon due to changes in flow conditions.
-
Flow Conditions: Classification based on Froude number - subcritical, critical, and supercritical.
-
Best Hydraulic Cross Sections: Optimal shapes to minimize construction costs while efficiently handling flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a rectangular channel with a flow depth of 2 meters and a velocity of 3 m/s, calculate the specific energy: E = y + (v^2 / 2g) where g = 9.81 m/s².
-
A sluice gate creates a transition from a supercritical flow (v = 15 m/s, y = 0.5 m) to a subcritical flow downstream. Calculate the new depth given specific energy considerations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In open channels, energy swings, with depth and speed, flow brings. Jump from super to sub, oh what a sight, losing energy, but it's alright!
📖 Fascinating Stories
-
Imagine a river flowing steadily, but suddenly it hits a drop—this causes a hydraulic jump! As the water cascades down, it swirls and roars, mixing air and losing energy, changing the flow forever.
🧠 Other Memory Gems
-
Remember JUMP for hydraulic jumps: J for Jump, U for Upstream to Downstream transition, M for Mixing action, P for Pressure energy loss.
🎯 Super Acronyms
Use FCS to remember Flow Conditions
- F: for Froude
- C: for Critical
- S: for Sub/Supercritical.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Specific Energy
Definition:
The total energy of flow per unit weight of fluid, consisting of flow depth and velocity head.
-
Term: Froude Number
Definition:
A dimensionless number that characterizes the flow regime; calculated as velocity divided by the square root of gravitational acceleration times flow depth.
-
Term: Hydraulic Jump
Definition:
An abrupt transition in the flow from supercritical to subcritical that results in energy loss and turbulence.
-
Term: Subcritical Flow
Definition:
Flow conditions where the Froude number is less than 1, often characterized by slower flow velocities.
-
Term: Supercritical Flow
Definition:
Flow conditions where the Froude number is greater than 1, characterized by higher velocities and lower depths.
-
Term: Critical Flow
Definition:
Flow conditions where the Froude number equals 1, signifying a balance between inertial and gravitational forces.
-
Term: Best Hydraulic Cross Section
Definition:
The optimal shape for a hydraulic conduit that minimizes construction costs while maximizing hydraulic efficiency.