Momentum Equations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Momentum Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're discussing momentum equations specifically in the context of fluid mechanics. Can anyone tell me the significance of momentum equations?

They help us understand how forces act on fluids.

Exactly! Momentum equations allow us to analyze how forces impact fluid motion and are critical when examining scenarios like open channel flows.

What about conservation of mass? How does that fit into momentum equations?

Great question! The conservation of mass is often the first equation we consider. In fluid dynamics, it translates into the continuity equation, which states that mass inflow must equal mass outflow.

Can you give us an example of this in action?

Certainly! An example would be the flow regulation at a sluice gate — as the flow depth decreases at the gate, the outflow velocity increases. Remember this as the principle where depth decreases leads to velocity increases!

Ah, like the saying 'decrease the depth, increase the speed'!

Exactly! That's a great memory aid!

To conclude this session, momentum equations help us analyze how forces and flow rates interact in fluid motion. Understanding mass conservation is fundamental for grasping more complex fluid behavior.
Specific Energy and Flow Depth Variations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s talk about specific energy. How do we define it in the context of open channels?

It's the total mechanical energy of the flow per unit weight of fluid.

Correct! Specific energy is critical because it allows us to understand how energy levels change with depth and flow velocity. Can someone elaborate on what happens when we visualize the specific energy curve?

I think it shows how energy behaves relative to the flow depth, right? The curves can intersect when conditions change.

Yes! It's particularly important in identifying critical depths where flow transitions can occur.

Do these transitions affect water flow much?

Absolutely! Transitions such as from subcritical to supercritical flow result in significant turbulence and energy losses, which we often see during hydraulic jumps.

So, if specific energy is high and depth is low, we have high velocity and possibly a hydraulic jump?

You've got it! As water moves from a high-energy state to a low one, it can create turbulence and a visible jump in flow.

In summary, understanding specific energy and its relationship to flow depth allows us to predict behavior in open channels, especially during transitions.
Hydraulic Jumps
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, we'll explore hydraulic jumps. Who can define what a hydraulic jump is?

It's a sudden change in flow from supercritical to subcritical, usually causing turbulence.

That's correct! Hydraulic jumps create energy losses due to turbulence. Can anyone explain what might cause these jumps?

I've read that they can be caused by changes in channel geometry, like a sudden drop or a narrowing?

Yes! That's a key point. Changes in channel geometry can lead to these rapid shifts in flow behavior.

What kind of problems can hydraulic jumps cause in engineering?

They can lead to erosion, flooding, or loss of energy efficiency in hydraulic systems. It's crucial to design channels to manage these impacts.

How can engineers control or utilize hydraulic jumps?

Great question! Engineers often design spillways and weirs to create controlled jumps that dissipate energy safely and minimize damage.

In summary, hydraulic jumps are vital to understanding flow transitions in open channels, and their careful management is crucial in engineering applications.
Optimizing Hydraulic Cross Sections
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s delve into the design of hydraulic cross sections. Why is it important to optimize these sections?

Optimizing cross sections can help minimize costs while ensuring efficient flow.

Exactly! The goal is to create a design that allows maximum flow efficiency while minimizing construction and maintenance costs.

What shapes are considered optimal for cross sections?

Commonly discussed shapes include rectangular, trapezoidal, and circular. Each has its advantages depending on the application.

How does the hydraulic radius affect design?

The hydraulic radius is crucial because it impacts the velocity of flow; maximizing it leads to better channel performance.

Are there any specific ratios we need to adhere to?

Yes! Different ratios and relationships can dictate the best conditions for flow and minimal perimeter.

So to wrap up, optimizing hydraulic cross sections focuses on balancing cost, efficiency, and flow dynamics.
Application of Momentum Equations in Real Life
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let’s connect momentum equations to real-world applications. What are some scenarios where we apply these principles?

One example is in designing drainage systems for urban environments.

Absolutely! Momentum equations play a significant role in ensuring efficient drainage that can prevent flooding.

Are these equations also used in larger structures like dams?

Yes, definitely. In dam design, these equations help calculate expected flows and manage energy dissipation effectively.

What kind of simulations or software could help with these calculations?

There are specialized hydrodynamic modeling software tools that engineers use to simulate flow behavior under various conditions.

How do engineers predict the impacts of hydraulic jumps in these applications?

By incorporating hydraulic jump equations into their models, engineers can anticipate energy losses and take measures to mitigate any negative effects.

To sum it up, momentum equations not only frame our theoretical understanding but also guide practical applications in hydraulic engineering.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section provides an overview of momentum equations applied to one-dimensional, incompressible, and steady flow in open channels. Key concepts include conservation of mass and energy, specific energy relations, hydraulic jumps, and optimal hydraulic cross-sections for canal design.
Detailed
Momentum Equations
This section dives deep into the momentum equations within the framework of fluid mechanics, specifically applied to open channel flow scenarios. The primary focus is on the derivation and application of conservation laws — both mass and energy — to understand fluid behavior in various hydraulic conditions.
Key Points Covered:
- One-Dimensional Flow: The section emphasizes the simplification of fluid flow to one dimension, which makes it easier to derive relevant equations and understand fluid motion.
- Conservation Equations: Important relationships derived from mass (continuity equation) and energy conservation are discussed, including how they relate to flow parameters like velocity and depth.
- Specific Energy: Significant energy concepts are introduced, discussing how specific energy affects flow depth variations and the transitions between critical and supercritical flow regimes.
- Hydraulic Jumps: The phenomenon of hydraulic jumps — where there is a transition from supercritical to subcritical flow — is explained, highlighting both energy losses and the turbulence generated during these jumps.
- Channel Design and Optimization: The section concludes with best practices for hydraulic cross-section optimizations that minimize construction costs while maintaining an efficient flow regime.
Youtube Videos





![Deriving Bernoulli's Equation in 1 Video [Physics of Fluid Mechanics #53]](https://img.youtube.com/vi/KuuLwRt6LQ4/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Conservation of Mass and Energy
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
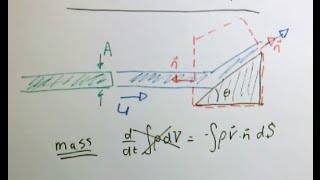
The basic concept what we use is we will talk about the conservations of mass and energy equations. So these two equations as we consider for the one-dimensional flow that is what we have simplified it one-dimensional incompressible okay steady flow.
Detailed Explanation
The section introduces the fundamental principles of fluid mechanics known as the conservation of mass and energy. In open channel flow, we simplify our analysis to a one-dimensional, incompressible, and steady state. This means that we assume the flow is steady over time and that the density of the fluid remains constant. Conservation of mass means that the mass entering a certain volume must equal the mass exiting it, which can be formulated mathematically.
Examples & Analogies
Think of a water hose: when you squeeze the end, the same amount of water must exit the hose as you allow to enter. If you constrict the flow, the water moves faster out of the hose, demonstrating the conservation of mass.
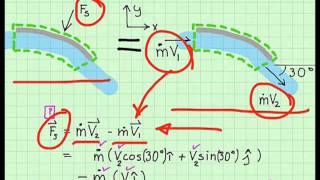
Forces Governing Open Channel Flow
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The basic idea to know it, the flow depth variations in open channels, the velocity variations, how the velocity changes it, how much of energy losses, okay. losses is happening it because of the flow and mostly it is governed by the gravity forces and the frictional forces as I discussed earlier.
Detailed Explanation
In open channel flow, changes in flow depth and velocity are primarily influenced by two forces: gravity and friction. Gravity causes water to flow downhill, which is why we have variations in depth and velocity as the water moves. Friction, on the other hand, acts against the flow and leads to energy losses. Understanding these forces helps us predict how water will behave in various engineering applications.
Examples & Analogies
Imagine a water slide: as you go down, gravity pulls you faster down the slide, but the friction of the slide slows you down. The interplay between gravity and friction determines how fast you reach the bottom.
Concept of Specific Energy
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The specific energy which is a graphical representations of energy versus the flow depth of a channel cross section where the datum is considered is a channel bottoms more or less the horizontal channel slopes.
Detailed Explanation
Specific energy is a concept that relates the energy in a flowing body of water to its depth. It is often represented in a graph that shows how energy varies with depth at a certain cross-section of a channel. The lower the specific energy, the more efficient the flow is. This concept helps engineers understand how water will react to changes in depth, helping inform designs for channels, spillways, and other structures.
Examples & Analogies
Think of a water fountain: the height of the water can represent energy. When the water is low (like when it's just barely splashing), it's less energetic compared to a steady gush that shoots high into the air, representing higher specific energy.
Flow Regimes: Subcritical, Critical, and Supercritical Flow
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Subcritical flow that means when you have a flow proud number lesser than 1... supercritical flow where the flow proud numbers is greater than 1.
Detailed Explanation
Flow in an open channel can be classified into three regimes based on the Froude number: subcritical (Froude number < 1), critical (Froude number = 1), and supercritical (Froude number > 1). Subcritical flow occurs at low velocities with deep flow depths, while supercritical flow occurs at high velocities with shallow flow depths. Critical flow is a transitional state where the velocity of the water matches the speed of the surface wave. Understanding these regimes is crucial for predicting flow behavior and ensuring that engineering designs can handle varying flow conditions.
Examples & Analogies
You can relate this to a car on a hill: when it moves slowly, it’s like subcritical flow, cruising along comfortably. At a flat speed where the car can just roll down, that’s critical flow. If the car speeds down the hill quickly, nearly flying off the slope, that’s like supercritical flow.
Hydraulic Jumps
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When the flow changes from supercritical to subcritical with a very limited ranges then there are a lot of turbulent structures created... the noise, the turbulence structures all you can see today is okay because you have a lot of sources like Google and YouTube.
Detailed Explanation
A hydraulic jump occurs when flow transitions from supercritical conditions to subcritical conditions, resulting in turbulent mixing and energy loss. This phenomenon creates distinct features in the water flow, such as sudden increases in depth and velocity changes. Hydraulic jumps are common in engineering structures like spillways and can even create noise and air bubbles in the water, enhancing aeration. Understanding hydraulic jumps is essential for managing flow energy and ensuring safe and effective designs.
Examples & Analogies
Consider a waterfall: as the water flows over the edge, it falls quickly (supercritical flow), then splashes into the pool below (subcritical flow). This splash creates turbulence and commotion, just like a hydraulic jump, mixing air into the water and creating a beautiful display.
Key Concepts
-
Momentum Equation: Expresses the balance of forces and fluid motion.
-
Specific Energy: Determines flow characteristics and energy levels.
-
Hydraulic Jump: Transition causing turbulence and energy loss.
-
Froude Number: Indicates the state of flow, critical for analyzing flow behavior.
-
Hydraulic Radius: Influences flow velocity and channel design.
Examples & Applications
Calculating flow in a sluice gate scenario where decreasing depth results in increased velocity.
Analyzing a hydraulic jump as water transitions from a spillway into a calmer pool.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In open channels swift and bright, / Jumping flows create a sight. / When super hits sub, watch the splash, / Energy lost, but in a flash!
Stories
Once in a river, a quick-flowing stream thought it could pass through a narrow channel easily. But as it jumped into calmer waters, turbulence brewed, causing energy loss, but ultimately shaping the riverbed.
Memory Tools
For Froude: 'Fast Flow Rest, Under Gravitational Ease' to remember subcritical, critical, and supercritical conditions.
Acronyms
MESH
Momentum
Energy
Specific energy
Hydraulic jump.
Flash Cards
Glossary
- Momentum Equation
An equation that expresses the conservation of momentum principle applied to fluid flow.
- Specific Energy
The total mechanical energy per unit weight of fluid, essential in studying fluid flow in open channels.
- Hydraulic Jump
A sudden transition from supercritical flow to subcritical flow in open channels, often resulting in turbulence and energy loss.
- Froude Number
A dimensionless number that indicates the flow regime of a fluid, defined as the ratio of flow velocity to the wave speed.
- Hydraulic Radius
The ratio of the cross-sectional area of flow to the wetted perimeter, important for determining flow characteristics.
Reference links
Supplementary resources to enhance your learning experience.
