Today we are discussing noncircular conduits and how they differ from circular ones. Noncircular conduits require us to define what we call a hydraulic diameter, which is essential for our calculations.

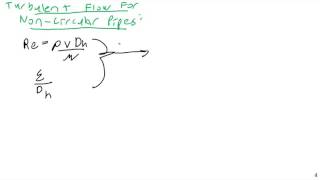
Great question! The hydraulic diameter is defined as four times the flow area divided by the wetted perimeter. It helps in understanding the flow characteristics in any sufficiently complex geometry.

The shape directly influences both the flow area and wetted perimeter. For instance, in a rectangular conduit, you'll need the rectangle's width and height to calculate those measurements.

Sure! For a rectangle with width 'b' and height 'h', the hydraulic diameter, Dh, can be calculated as 4Ah/P. Remember, Ah is the area and P is the wetted perimeter, which in this case is '2b + 2h'!

In summary, understanding the hydraulic diameter is crucial for analyzing fluid behavior in noncircular conduits.

Today, let's discuss the impact of pipe roughness on fluid flow, building on the work of Nikuradse, who conducted significant experiments back in the 1930s.

Nikuradse introduced roughness elements like sand grains in pipes to study their impact on flow. He discovered that as roughness increased, it affected the friction factors and overall energy losses.

When calculating friction factors for turbulent flow, you can see how roughness interacts with Reynolds numbers. The greater the roughness and flow velocity, the more significant the friction losses will be.

Understanding how roughness impacts flow helps engineers design systems that minimize energy losses, ensuring efficiency in processes like water supply and sewage treatment.

To summarize, roughness can significantly influence fluid flow dynamics, which is crucial for practical applications.

Let’s explore how velocity distribution behaves under turbulent flow conditions.

In laminar flow, velocity is typically parabolic in shape, while in turbulent flow, it becomes flatter – with most flow occurring in the center of the conduit.

Great point! The Reynolds number indicates the flow regime. For instance, a Reynolds number below 2000 typically indicates laminar flow, while above 4000 signifies turbulent flow.

It's often expressed in non-dimensional forms to relate wall shear stress, hydraulic diameter, and flow conditions, essential for calculations.

In summary, turbulence significantly modifies velocity distribution in fluids, heavily influenced by both fluid and conduit characteristics.

Today we'll discuss wall shear stress, a critical concept when analyzing noncircular conduits.

Wall shear stress is the force exerted by the fluid on the walls of the conduit. It's crucial for predicting energy losses in flow.

It can be derived from empirical relationships involving average velocities and hydraulic radius, often expressed through parameters like Reynolds number.

By understanding wall shear stress, engineers can design systems that operate efficiently, addressing concerns like energy consumption and flow stability.

In conclusion, recognizing and calculating wall shear stress is vital in fluid mechanics, particularly with noncircular conduits.

In our final session, let's discuss how these concepts from today apply to real-world scenarios.

Certainly! Noncircular conduits are common in sewage systems, where various shapes accommodate different flow characteristics.

In designs for water treatment plants, understanding flow characteristics helps minimize sedimentation and optimize chemical dosing.

Understanding the impact of conduit shape on flow helps engineers make informed decisions to create efficient, robust systems.

In summary, applying fluid mechanics principles to real-world situations allows us to improve infrastructure efficiency and effectiveness.