Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Turbulent Flow and Noncircular Conduits
Unlock Audio Lesson
Today we're going to explore turbulent flow, especially how it behaves in noncircular conduits. Can anyone explain what turbulent flow is?
Turbulent flow is chaotic and irregular, unlike laminar flow, which is smooth and orderly.
Exactly! In turbulent flow, velocity changes unpredictably. Now, when dealing with conduits that aren't circular, what do we use to describe their characteristics?
We use hydraulic diameter to analyze flow in those conduits.
Correct! The hydraulic diameter is essential for noncircular shapes. Remember this acronym: 'A/W' - Area over Wetted perimeter. Can anyone give me an example of hydraulic diameter calculation?
For example, if we have a rectangular conduit, we would calculate it based on the width and height.
Great example! Let's recap: turbulent flow is chaotic, and hydraulic diameter helps us analyze flow in noncircular conduits.
Nikuradse's Experiments and the Moody Chart
Unlock Audio Lesson
Nikuradse's experiments in the 1930s provided invaluable insights into turbulent flow. Can anyone tell me how his work impacts our understanding today?
He established empirical relationships that now help us use Moody's chart for friction factors.
Exactly! Moody's chart helps us visualize how friction factors correlate with Reynolds numbers. Why is this important for engineers?
It allows us to predict energy losses in pipe flows, which is crucial for designing efficient systems.
Right! Engineers rely on these relationships for effective design and analysis. Remember, understanding turbulence is key for any fluid flow system!
Velocity Distribution and Wall Shear Stress
Unlock Audio Lesson
Let's now focus on how velocity distribution and wall shear stress behave in turbulent flow. How do these properties differ from laminar flow?
In turbulent flow, the velocity distribution is flatter, while in laminar flow, it's more parabolic.
Good observation! In turbulent flow, the wall shear stress tends to be more uniform along the wall, while laminar flow has maximum shear at the edges. Can anyone diagram this?
Sure! I can draw the velocity profile for both flows, showing those differences.
Fantastic! This visual representation reinforces our understanding of flow behavior. Always remember this contrast!
Applying Knowledge: Solving Problems in Noncircular Conduits
Unlock Audio Lesson
Now that we understand the concepts, let's apply them! How would you determine wall shear stress in a triangular conduit?
We would need to calculate the hydraulic diameter first and then apply relevant formulas from the Moody chart.
Exactly! Why is it critical to define the shape of the conduit accurately?
Because the shape affects the fluid's velocity profile and energy losses!
Perfect! Every detail counts in fluid mechanics. Let's take a moment to summarize what we learned today!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The text examines how turbulent flow behaves in noncircular conduits, highlighting methods for calculating relevant parameters like hydraulic diameter, wall shear stress, and utilizing Moody's chart for flow analysis. Additionally, it reflects on historical experiments that established foundational principles in fluid mechanics.
Detailed
In this section of Fluid Mechanics, the focus is on understanding turbulent flow specifically in noncircular conduits. Turbulent flow can exhibit different characteristics compared to laminar flow, significantly influenced by the conduit shape and roughness. The section introduces the concept of hydraulic diameter (a function of the cross-sectional area and wetted perimeter), essential for characterizing noncircular conduits. Additionally, it discusses the historical context of turbulent flow analysis through Nikuradse's fundamental experiments, illustrating how they led to important relationships such as the Moody chart that links friction factors with Reynolds numbers. It also details velocity distributions and shear stress profiles, distinguishing between laminar and turbulent profiles and explaining how these properties change depending on flow conditions and conduit geometry. Overall, this section is vital for understanding the complexities of turbulent flow in various geometrical configurations, helping students relate theory to practical applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Noncircular Conduits
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now coming to the noncircular conduits, many of the times also we do not go for only the circular conduits or the circular pipes from one point to other points okay.
Detailed Explanation
In fluid mechanics, flow is often considered through circular pipes. However, there are instances where we deal with noncircular conduits. These can include rectangular, triangular, or any other non-round shapes. Such conduits present unique challenges, and the principles used for circular pipes may need adaptation for noncircular configurations.
Examples & Analogies
Think of water flowing through a garden hose, which is circular, versus water flowing through a ditch that's rectangular in shape. Both will allow water movement, but the way they handle flow is very different due to their shapes.
Hydraulic Diameter
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
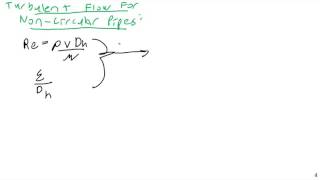
But when you go for a noncircular case you need to define as a equivalent flow okay. So that means we introduce a hydraulic diameters okay, it is called as hydraulic diameters, which is a functions of area and wetted perimeter.
Detailed Explanation
To analyze the flow in noncircular conduits, we often use a concept called 'hydraulic diameter.' This is defined using the cross-sectional area of flow and the wetted perimeter (the part of the perimeter that is in contact with the liquid). The hydraulic diameter allows us to convert the noncircular shape parameters into something we can analyze similarly to circular pipes.
Examples & Analogies
Imagine measuring the effectiveness of a straw versus a funnel. Both can hold and move liquid differently based on their shapes. The hydraulic diameter acts as a way of measuring how effectively a noncircular shape can move fluid in comparison to a circular one.
Effects of Shape on Flow Characteristics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look it that when you have a noncircular pipe like if you have a pipe like a triangular shape okay. So in this case what will happen the if you have a laminar flow you will have a wall stress will be maximum near the mid points of the sides.
Detailed Explanation
In noncircular pipes, like a triangular shape, the flow changes compared to a circular pipe. For laminar flow in triangular conduits, the wall shear stress (the frictional force exerted by fluid on the wall of the conduit) peaks at the midpoints of each side. This non-uniform distribution contrasts sharply with circular pipes, where the stress is distributed more evenly.
Examples & Analogies
Consider how a flowing river behaves at the bends and curves of its banks. Similarly, water flows differently around the edges of a triangular pipe, causing varying pressures and stresses, just as it does around the contours of the land.
Turbulent Flow Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look it that if you have the turbulent flow same case you have a turbulent flow the velocity distributions as well as the wall shear stress distributions exchanges it.
Detailed Explanation
In turbulent flow within noncircular conduits, the dynamics change significantly. Unlike laminar flow, turbulent flow has a more chaotic structure which leads to different velocity patterns and wall shear stress distributions. This means that the distribution of velocity is not uniform and changes interactively across the flow area.
Examples & Analogies
Think of mixing paint with a brush. When you stir gently, the paint moves predictably (laminar), but when you vigorously mix it, the colors swirl erratically (turbulent). This chaos in turbulent flow leads to different frictional effects in noncircular shapes.
Higher Reynolds Numbers Influence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now coming back to the velocity profile, or the shear stress at the boundary. Here we divide into two zones as suggested by Nikuradse by conducting a series of experiment, finding out velocity profiles for the turbulent flow where you have the flow Reynolds number less than three million.
Detailed Explanation
Nikuradse's experiments helped identify two distinct flow zones within turbulent conditions based on the Reynolds number. For Reynolds numbers below three million, the flow shows a certain velocity profile that's somewhat predictable, breaking into layers due to the varying speed throughout the cross-section of the pipe.
Examples & Analogies
Imagine layering different liquids in a jar. The lighter liquid floats on top, while the denser one settles at the bottom. Similarly, different flow velocities create distinct zones or layers in turbulent flow.
Shear Stress in Turbulent Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When you have the Reynolds numbers more than 3 millions, then there is certain zone of the velocity profile develops.
Detailed Explanation
For Reynolds numbers exceeding three million, the behavior of the flow adjusts further, resulting in more complex layers, especially adjacent to the wall of the conduit. In this region, the flow acts more like laminar, showcasing high viscosity until further away from the wall, where turbulence reigns free.
Examples & Analogies
Consider driving a car on a smooth highway versus off-roading through rough terrain. Close to the edges, it feels smooth, but in the middle of the chaos, it's a completely different experience of speed and pressure.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Turbulent Flow: Chaotic flow patterns with irregular velocity and pressure.
-
Hydraulic Diameter: A crucial calculation for noncircular conduits to analyze flow conditions.
-
Wall Shear Stress: Important for understanding energy losses and flow resistance in pipes.
-
Moody Chart: A tool for engineers to determine friction factors based on flow conditions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a rectangular channel, if the width is 2 m and height is 1 m, the hydraulic diameter would be calculated as (2*1)/(2+2) = 1 m.
-
In a triangular conduit with a base of 2 m and height of 1.5 m, the hydraulic diameter can be computed considering the wetted perimeter and area.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When the flow gets turbulent, oh what a sight, Energy loss increases, isn't that right!
📖 Fascinating Stories
-
Imagine a rush of water pushing through a narrow, rough tunnel. At first, it flows smoothly, then turbulence begins, splashes everywhere, showing how conduit shape can impact flow.
🧠 Other Memory Gems
-
Remember 'Hydraulic Helps' for Hydraulic diameter, Hydraulic radius, and Wall shear stress!
🎯 Super Acronyms
Use the acronym 'T-HEMW' – Turbulence, Hydraulic Diameter, Energy, Momentum, Wall shear stress to remember key concepts.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Turbulent Flow
Definition:
A type of fluid flow characterized by chaotic changes in pressure and velocity.
-
Term: Hydraulic Diameter
Definition:
A parameter used for noncircular conduits, defined as four times the cross-sectional area divided by the wetted perimeter.
-
Term: Wall Shear Stress
Definition:
The tangential force per unit area exerted by a fluid on the wall of its container.
-
Term: Moody Chart
Definition:
A graphical representation that shows friction factors for various flow regimes in pipes, dependent on Reynolds number and relative roughness.
-
Term: Reynolds Number
Definition:
A dimensionless quantity used to predict flow patterns in different fluid flow situations.