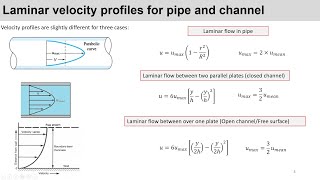
Velocity Profile for Laminar Flow
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Laminar Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll start by discussing laminar flow. Can anyone explain what defines laminar flow?

Isn't it when the fluid flows in parallel layers, and the flow is smooth?

Exactly, good! Laminar flow is characterized by orderly streamlines and occurs at lower Reynolds numbers. Now, how do we visualize the velocity profile in laminar flow?

It's a parabolic shape, right? The fluid moves fastest in the center and slowest at the boundary.

Correct! This will help us understand the concept of wall shear stress as well. A mnemonic to remember the velocity profile shape is 'Fast at the center, Slow at the edges—FSE'!

That makes it easier to remember! What about the impacts of pipe diameter?

Great question! The pipe diameter will affect the Reynolds number, which influences whether the flow remains laminar or becomes turbulent.

In summary, remember: Laminar flow is smooth and parabolic, with maximum velocity at the center, and this behavior leads to key applications in fluid mechanics.
Wall Shear Stress in Laminar Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's focus on wall shear stress in laminar flow. Can anyone tell me how it's defined?

It's the resistance caused by the viscosity of the fluid at the boundary of the cylinder, right?

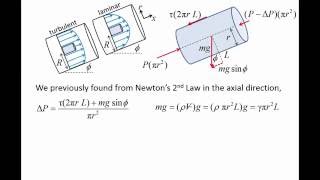
Exactly! The wall shear stress is directly related to the velocity gradient at the boundary. As we move away from the wall, the velocity increases until we reach the middle of the pipe.

So if the viscosity increases, will the wall shear stress also increase?

Correct! More viscosity means more resistance, thus higher wall shear stress. A helpful acronym is 'VIS' for 'Viscosity Increases Shear'.

Are there any equations that can help us calculate those values?

Yes, the equation τ_w = μ(dU/dy) evaluates wall shear stress. Here, τ_w is the wall shear stress, μ is the dynamic viscosity, and (dU/dy) is the velocity gradient.

In summary, wall shear stress increases with viscosity and is crucial for understanding flow behavior—especially for predicting behaviors in engineering applications.
Impact of Pipe Geometry on Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Lastly, let’s discuss how pipe geometry influences flow. What happens when we have non-circular conduits?

Do we need a hydraulic diameter for those?

Exactly! For non-circular conduits, the hydraulic diameter is used to analyze flow. Can anyone tell me how it’s calculated?

It's the area divided by the wetted perimeter, right?

Correct! And this hydraulic diameter becomes critical in determining flow velocities and shear stresses. An acronym to remember could be 'AP/WP'—Area per Wetted Perimeter.

And how does that relate back to the velocity profile?

Great connection! The velocity profile can vary significantly based on geometry. For instance, in a rectangular conduit, the velocity profile will spread out differently than in a circular pipe.

In summary, hydraulic diameter is essential for non-round conduits, influencing how velocity and shear characteristics manifest!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section elaborates on the concept of velocity profiles for laminar flows, particularly focusing on the impact of pipe geometry and Reynolds number. It explicates key definitions and empirical relationships established through experiments, particularly addressing how these influence wall shear stresses and flow characteristics in non-circular conduits.
Detailed
In this section, we delve into the intricate details of velocity profiles in laminar flow, particularly in relation to the pipe geometry and how it affects various parameters associated with fluid dynamics. The examination begins with a foundational understanding of the laminar flow regime, defined by low Reynolds numbers. The velocity profile is characterized as a parabolic shape, where the velocity is maximum at the center of the pipe and decreases towards the walls, ultimately reaching zero at the boundary due to the no-slip condition. The relationship between the wall shear stress and flow characteristics is also emphasized, referencing empirical relationships developed through experiments such as those by Nikuradse. Furthermore, the impact of conduit shape—forcing us to consider hydraulic diameters for non-circular pipes—is explored. Understanding these principles is essential for practical applications in fields like civil engineering, hydraulic design, and fluid transportation systems.
Youtube Videos






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Velocity Profiles
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
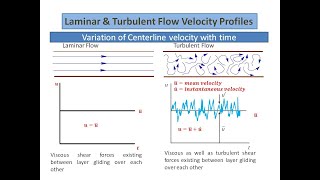
Velocity distributions in pipe flow can be categorized as laminar or turbulent. Laminar flow occurs at low Reynolds numbers, where fluid particles move in parallel layers, while turbulent flow happens at higher Reynolds numbers, characterized by chaotic motion.
Detailed Explanation
In fluid mechanics, the flow of liquid through a pipe can behave in distinct ways based on its speed and the characteristics of the pipe. For low flow speeds or small pipe diameters, the flow is termed 'laminar,' meaning the liquid moves in smooth, parallel layers. Conversely, at high speeds or larger sizes, the flow becomes 'turbulent,' marked by swirling and fluctuating motions.
Examples & Analogies
Imagine you are slowly pouring honey into a narrow tube. The honey flows smoothly in layers, which is like laminar flow. Now, think about rapidly shaking a bottle of salad dressing; it mixes chaotically and flows wildly, resembling turbulent flow.
Characteristics of Laminar Flow
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In laminar flow, the velocity profile is parabolic. The fluid moves fastest at the center of the pipe and slows down as it moves closer to the walls due to friction with the pipe surface.
Detailed Explanation
The parabolic velocity profile means that if you were to graph the speed of the fluid against the distance from the center of the pipe, you'd see a curve peaking in the middle and tapering off near the edges. This occurs because the layers of fluid closest to the pipe walls experience resistance due to friction, effectively slowing them down compared to layers in the center, which move with less obstruction.
Examples & Analogies
Think about how a crowd moves through a narrow exit. People in the center can move more quickly, while those along the sides slow down as they bump against the walls and each other, much like how the fluid behaves in laminar flow.
Empirical Relationships in Laminar Flow
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The relationship between the average velocity and the wall shear stress in laminar flow can be empirically established. This is done through experiments to develop a formula that links these two parameters.
Detailed Explanation
In hydraulic studies of laminar flow, researchers use real-life experiments to deduce how the average speed of a fluid correlates with the shear stress acting on the walls of the pipe. The shear stress is a measure of how much the fluid's movement is influenced by the surface of the pipe, and as the flow speed increases, so does the wall shear stress. These observations help form equations that can predict flow behavior based on varying conditions.
Examples & Analogies
Consider how a painter applies pressure to a roller as they paint a wall. If they push harder (akin to increasing fluid velocity), the paint comes off more easily, similar to how increased velocity results in greater shear stress on the pipe walls.
Transition to Turbulent Flow
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When the Reynolds number exceeds a critical threshold (around 2000 for circular pipes), laminar flow can transition into turbulent flow. This transition alters the velocity profile and shear stress distribution significantly.
Detailed Explanation
The Reynolds number is a dimensionless number that helps predict flow patterns in different fluid flow situations. A value below 2000 suggests laminar flow, while above that indicates a transition to turbulence. In turbulent flow, the previously smooth, parabolic velocity distribution becomes flatter, reflecting various speeds throughout the cross-section of the pipe due to chaotic mixing.
Examples & Analogies
Think of a calm lake that stays smooth until a speedboat races across it. At first, the wake spreads with smooth waves, but eventually, as the boat speeds up, the water churns and splashes wildly, analogous to how laminar flow transitions to turbulent flow.
Key Concepts
-
Velocity Profile: The distribution of fluid velocity across a cross-section of the conduit.
-
Hydraulic Diameter: A pivotal measurement in non-circular conduits, guiding flow analysis.
-
Wall Shear Stress: A crucial factor in flow resistance, reflecting how the fluid adheres to conduit walls.
Examples & Applications
In a circular pipe with laminar flow, the velocity distribution can be modeled as parabolic.
For a rectangle cross-section, the hydraulic diameter calculation is essential for understanding flow characteristics.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In laminar flow, smooth it goes, Fast at the center, slow it flows.
Stories
Imagine a smooth river where water glides past. This river is like laminar flow, with all water particles moving in harmony without disturbance.
Memory Tools
Use 'FSE' for 'Fast at the center, Slow at edges' to remember the laminar flow velocity profile.
Acronyms
Remember 'VIS'
Viscosity Increases Shear to recall that higher viscosity leads to higher wall shear stress.
Flash Cards
Glossary
- Laminar Flow
A flow regime characterized by smooth, orderly motion of fluid in parallel layers.
- Reynolds Number
A dimensionless number used to predict flow patterns in different fluid flow situations.
- Wall Shear Stress
The stress exerted by a fluid on the wall of a conduit due to viscosity.
- Hydraulic Diameter
A concept used for non-circular conduits, computed as the ratio of the area to the wetted perimeter.
Reference links
Supplementary resources to enhance your learning experience.
